数据结构第八章：栈与队列习题

一.题目一：括号匹配问题

题目介绍

给定一个只包括{ $(和)$ }的字符串s，判断字符串是否有效？

有效字符需要满足：左括号必须与相应的右括号闭合。左右括号必须以正确的顺序闭合。

示例

s=()---------输出：true

s=()\[\]{}-------输出：true

s=(]-----------输出：false

思路展示

该题目需要用到栈的知识，因为栈的特性是后进先出，让左括号进行入栈，遇到右括号开始判断，如果匹配则继续判断；不匹配则输出结果。

代码展示

cpp 复制代码

void StackInit(ST* ps)    //栈区的初始化
{
  assert(ps);
  ps->a=(STDataType *)malloc(sizeof(STDataType)*4);
  ps->capacity=4;
  ps->top=0;
}

void StackDestory(ST *ps)    //栈区的销毁
{
  assert(ps);
  free(ps->a);
  ps->a=NULL;
  ps->top=ps->capacity=0;
}

void StackPush(ST *ps,STDataType x)    //栈区的插入
{
  assert(ps);
  if(ps->top==ps->capacity)
  {
    STDataType *tmp=(STDataType *)realloc(ps->a,ps->capacity*2*sizeof(STDataType));
    if(tmp==NULL)
    {
      printf("realloc fail!");
      exit(-1);
    }
    else 
    {
      ps->a=tmp;
      ps->capacity*=2;
    }
  }
  ps->a[ps->top]=x;
  ps->top++;
}

void StackPop(ST *ps)    //栈区的删除
{
  assert(ps);
  assert(ps->top>0);
  ps->top--;
}

STDataType StackTop(ST *ps)//获取栈顶部的元素
{
  assert(ps);
  assert(ps->top>0);
  return ps->a[ps->top-1];
}

int StackSize(ST *ps)    //获取栈的大小
{
  assert(ps);
  return ps->top;
}

bool StackEmpty(ST* ps)    //判断栈区是否为空
{
  assert(ps);
  return ps->top==0;
}

bool isValid (char *s)//括号匹配函数
{
    ST st;    //创建一个栈
    StackInit(&st);    //对栈进行初始化
    while(*s!='\0')    //参数不为\0时，进去循环，进行进一步的括号匹配判断
    {
        switch(*s)

        {
            case '('：
            case '[':
            case '{':    //如果为左括号则调用插入函数，将左括号插入在栈内，等待进一步的判断
            {
                StackPush(&st,*s)
                ++s;
                break;
            }
            case ')':
            case ']':
            case '}':    //如果为右括号，则取出栈顶元素与此时的右括号进行比对，如果对应则进行下一步判断。否则输出匹配失败的信息。
            {
                if(StackEmpty(&st))
                {
                    StackDestory(&st);
                    return false;
                }
                char top=StackTop(&st);
                StackPop(&st);
                else
                {
                    ++s;
                }
                break;
            }
        } 
    
    }

    bool ret=StackEmpty(&st);    //如果栈是空的说明括号不匹配，反之括号检查完毕，为匹配。
    StackDestory(&st);    //检查括号匹配之后，需要对栈进行销毁。
    return ret;    
}

上述代码的具体解释：因为我们学习初阶数据结构的语言基础为C语言，C语言不可以调用库，所以需要我们将栈的相关代码尽数拷贝到所写代码前面。

下面详细讲解一下我们最后一个函数：括号匹配函数。此函数运用到了栈的后进先出的基本特性。括号匹配问题化简之后就是，出现第一个右括号时，与上一个左括号进行比对。以此类推。当每个括号都比过一次，则可以得到匹配的结果。当然，如果中途出现括号不匹配的情况可以直接结束判断，直接输出false。

题目二：用队列实现栈

题目介绍

请你仅使用两个队列实现一个具有后进先出特性的栈结构

思路展示

队列的特性是先进先出，栈的特性是后进先出。可以根据两者的特性进行进阶的变化，下面将画图展示该变化。

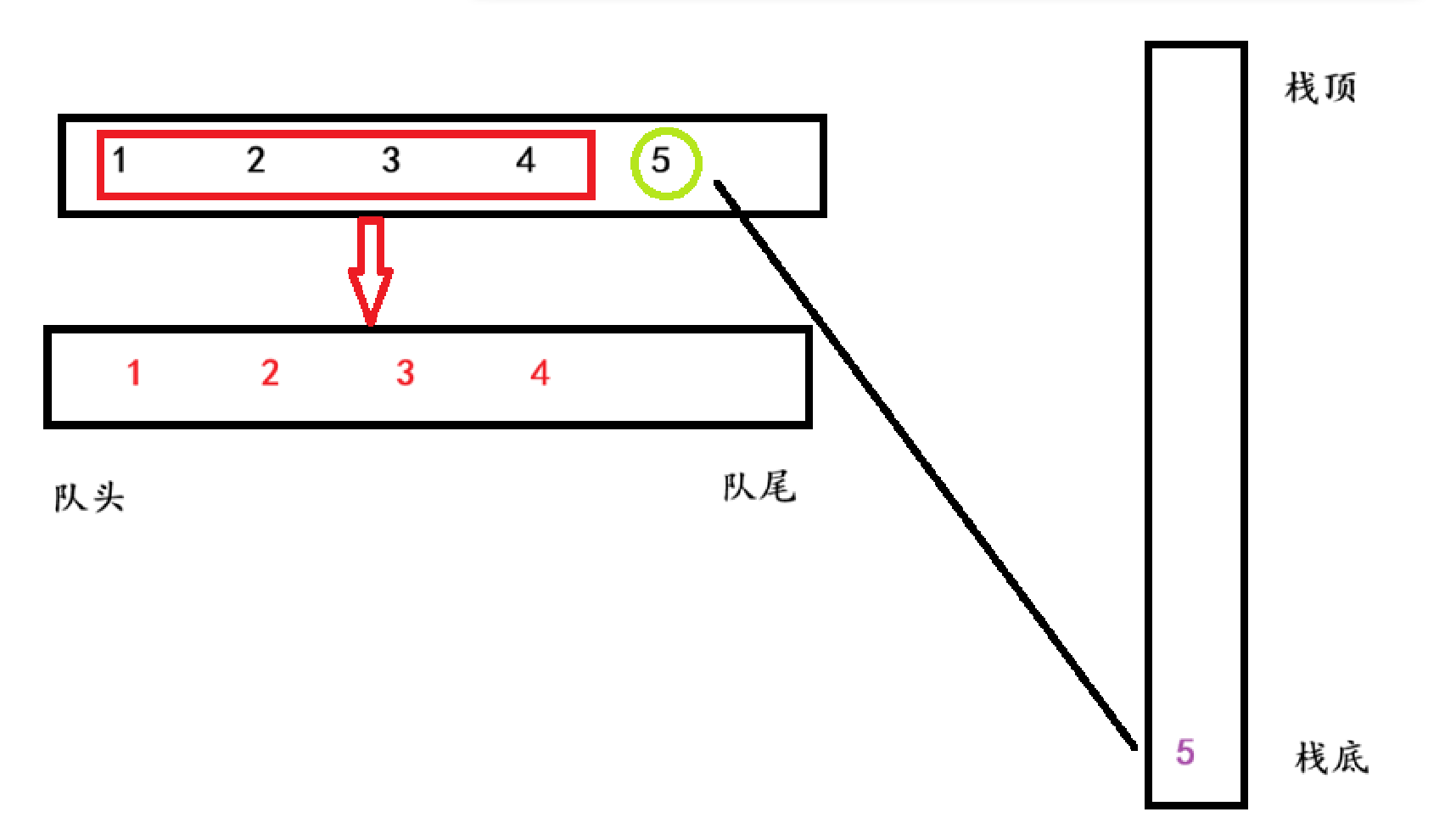
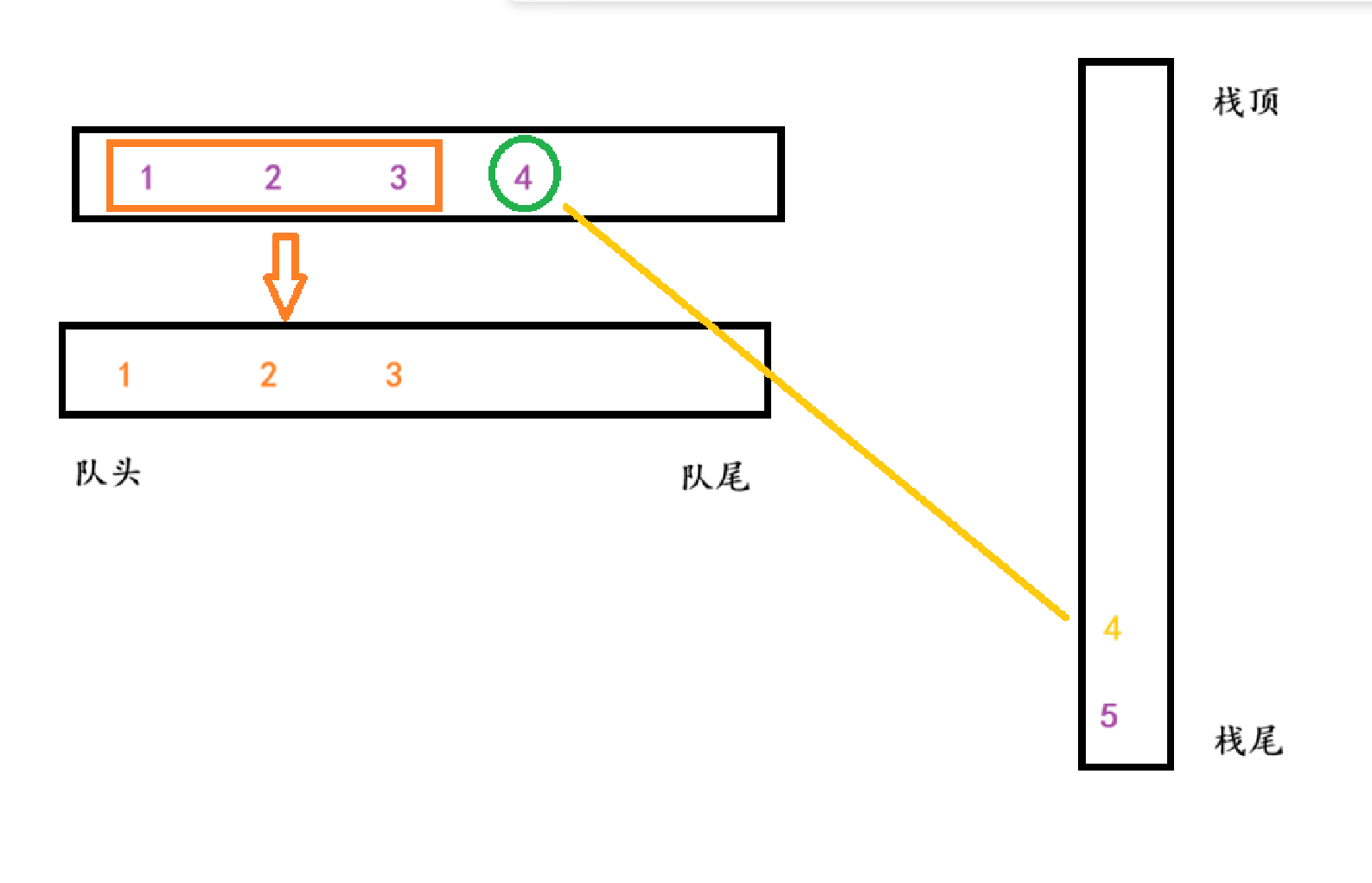
代码展示

cpp 复制代码

void QueueInit(Queue *pq)    //队列的初始化
{
  assert(pq);
  pq->head=pq->tail=NULL;
}

void QueueDestory(Queue *pq)    //队列的销毁
{
  assert(pq);
  QNode* cur=pq->head;
  while(cur)
  {
    QNode* next=cur->next;
    free(cur);
    cur=next;
  }
  pq->head=pq->tail=NULL;
}

void QueuePush(Queue* pq,QDataType x)    //队列的插入
{
  assert(pq);
  QNode* newnode=(QNode*)malloc(sizeof(QNode));
  if(newnode==NULL)
  {
    printf("malloc fail");
    exit(-1);
  }
  newnode->data=x;
  newnode->next=NULL;
  if(pq->tail==NULL)
  {
    pq->head=pq->tail=newnode;
  }
  else
  {
    pq->tail->next=newnode;
    pq->tail=newnode;
  }
}

void QueuePop(Queue* pq)    //队列的删除
{
  assert(pq);
  assert(pq->head);
  if(pq->head->next==NULL)
  {
    free(pq->head)
    pq->head=pq->tail=NULL;
  }
  else
  {
    QNode* next=pq->head->next;
    free(pq->head);
    pq->head=next;
  }
}

QDataType QueueFront(Queue* pq)    //获取队头元素
{
  assert(pq);
  assert(pq->head);
  return pq->head->data;
}

QDataType QueueBack(Queue *pq)    //获取队尾元素
{
  assert(pq);
  assert(pq->head);
  return pq->tail->data;
}

int QueueSize(Queue* pq)    //获取队列的大小
{
  assert(pq);
  int size=0;
  QNode* cur=pq->head;
  while(cur)
  {
    ++size;
    cur=cur->next;
  }
  return size;
}

bool QueueEmpty(Queue* pq)    //判断队列是否为空
{
  assert(pq);
  return pq->head==NULL;
}


typedef struct    //有两个队列的结构体
{
  Queue q1;
  Queue q2;
} Mystack;

MystackCreat()    //栈的初始化
{
  Mystack *ps =(Mystack *)malloc(sizeof(Mystack));
  if(ps==NULL)
  {
    printf("malloc fail!");
    exit(-1);
  }
  QueueInit(&ps->q1);
  QueueInit(&ps->q2);
  return ps; 
}

void myStackPush(Mystack *obj,int x)    //栈的插入数据
{
  if(!QUEUEmpty(&obj->q1))
    QueuePush(&obj->q1,x);
  else 
    QueuePush(&obj->q2,x);
}

int mystackPop(MYstack *obj)    //队列的倒数据
{
  Queue *emptyQ = &obj->q1;
  Queue *nonemptyQ = &obj->q2;
  if(!QueueEmpty(&obj->q1))
  {
    emptyQ = &obj->q2;
    emptyQ = &obj->q1;
  }
  while(QueueSize(nonemptyQ)>1)
  {
    QueuePush(emptyQ,QueueFront(nonemptyQ));
    QueuePop(nonemptyQ);
  }
  int top = QueueFront(nonemptyQ);
  QueuePop(nonemptyQ);
  return top;
}

int mystack(Mystack *obj)    //返回栈元素
{
  if(!QUEUEmpty(&obj->q1))
    QueueBack(&obj->q1);
  else 
    QueueBack(&obj->q2);
}

bool mystackEmpty(Mystack *obj)    //判断栈是否为空
{
  return QueueEmpty(&obj->q1) && QueueEmpty(&obj->q2);
}

void mystackFree(Mystack *obj)    //释放栈空间
{
  QueueDestory(&obj->q1);
  QueueDestory(&obj->q2);
  free(obj);
}

上述代码的具体解释：在栈的初始化函数中，需要将结构体内的成员变量进行初始化，（将两个队列进行相应的初始化）；栈插入数据函数，需要将非空队列的末尾元素插入。所以需要将非空队列的元素悉数挪动到空队列中，剩余的最后一个元素插入栈中；栈的插入需要队列间不停的倒腾数据，所以直接写出新函数，用于队列数据间的倒腾过程。倒腾数据需要将非空队列的元素（除去最后一个元素以外）都置于空队列中；返回栈的元素实际上是返回非空队列的队尾元素，所以在返回栈元素的函数中直接调用返回队列尾部元素的函数即可；判断栈是否为空的函数，只需要判断两队列是否为空即可；释放栈的空间函数，需要先释放掉队列对应的链表，最后再释放掉栈指针。

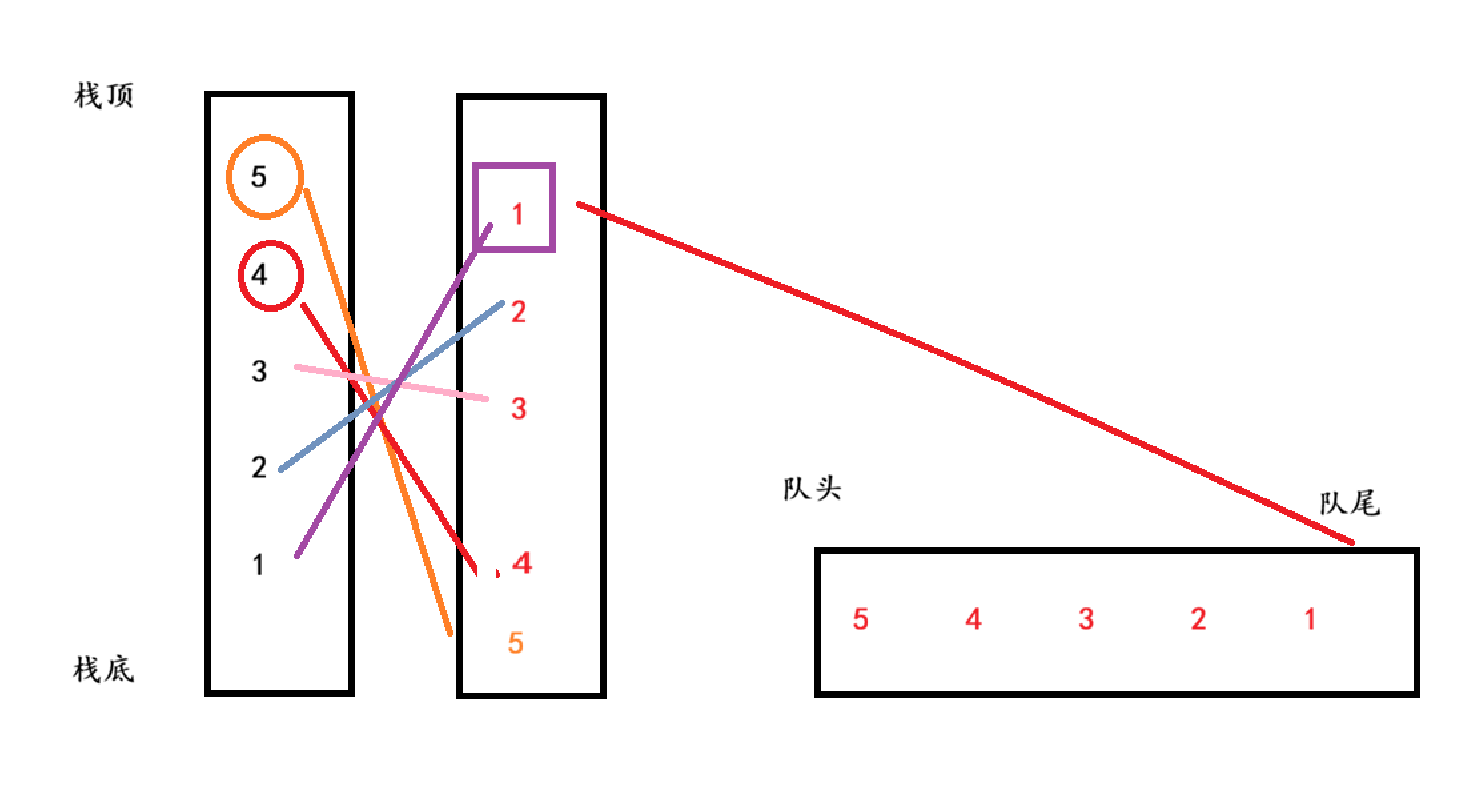
题目三：用栈实现队列

题目介绍

请你仅使用两个栈实现一个具有先进先出特性的队列结构

思路展示

因为队列的特性是先进先出，栈的特性是后进先出。所以需要将栈进行一次数据的颠倒即可插入队列当中，因为思路和题目二一致，所以仅仅给出图片解释：