一、"树"是什么
树(Tree) 是一种非线性、分层级的数据结构,它模拟了自然界中树的分支结构。核心特点是:一个节点可以有多个后继(子节点),但只能有一个前驱(父节点)。树结构是递归定义的。
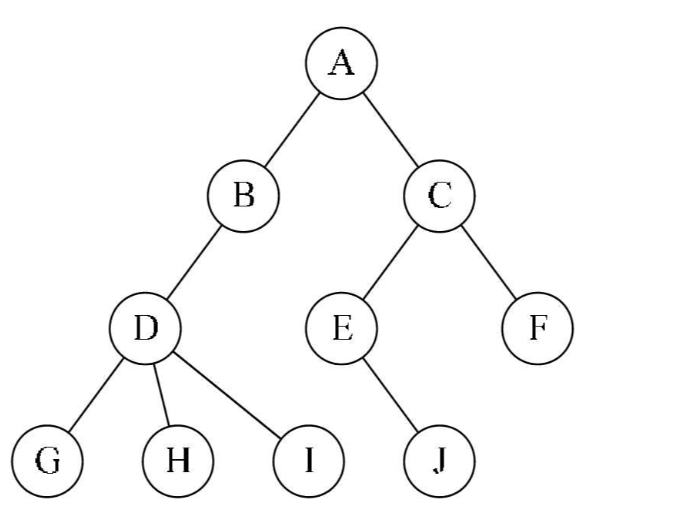
如图,就是一棵树。
二、"树"的理解
我们可以把树想象成宗族关系
- :A是整棵树的"根",我们称A为
根节点------相当于A是整个家族的老祖宗。 - 对根节点以外的任意节点,都有
父节点------除了老祖宗可能是石头缝里蹦出来的,其他人都得由父母生出来。 - 节点不一定都有
子节点- 没有子节点的,我们称为
叶节点或终端节点 - 有子节点的,我们称之为
非叶子节点或分支节点
- 没有子节点的,我们称为
兄弟节点:同一个父节点的孩子我们称之为兄弟节点- 在树形结构中,"大小"或"远近"这种关系
仅在同一路径上具有明确的传递性------正如你必定比你的直系祖先(父亲、祖父)年轻,但你完全有可能比你叔叔(另一分支上的节点)年长!

三、树的基础概念
1. 度
-
节点的度:该节点拥有的子节点数量
- 例:某节点有2个子节点,则该节点的度为2
-
树的度:树中所有节点的最大度值
- 例:某树中所有节点的度最大为4,则该树的度为4
2. 层次与深度
-
层次:根节点为第1层,其子节点为第2层,以此类推
-
节点的深度:从根节点到该节点的路径长度(边数)
- 根节点的深度为0或1(定义不同,常见为0)
3. 高度
-
节点的高度:从该节点到最深叶子节点的最长路径长度
-
树的高度:根节点的高度
- 叶子节点的高度通常为0或1
4. 路径
-
路径:从一个节点到另一个节点的节点序列
-
路径长度:路径上的边数
5. 子树
- 子树:树中任意节点及其所有后代构成的子结构
四、树节点的表示
理解树简单,但想实现树就有难度了
- 比如:在定义树节点结构体的时候,我们应该如何定义呢。
首先,我们还是要有数据域和指针域:
数据域很简单,就是存放当前节点的数据
- 而让人困惑的点在于
节点的指针域设计:我们确实需要存储子节点的引用,但由于每个节点可能拥有数量不确定的子节点,我们无法预先为一个节点分配固定大小的指针空间来存放所有子节点地址。这种不确定性使得简单的固定长度指针数组变得不可行。
- 所以有人想出了一个非常巧妙的方法------左孩子右兄弟
- 在左孩子-右兄弟表示法中,我们为树的每个节点设计两个指针域:
- 左指针:指向该节点的
第一个子节点(即"长子")。 - 右指针:指向该节点在
兄弟节点中的下一个兄弟。
- 左指针:指向该节点的
- 在左孩子-右兄弟表示法中,我们为树的每个节点设计两个指针域:
- 通过这种方式:
- 节点的所有子节点被组织成一个以第一个子节点为起点的单链表。
- 每个子节点的右指针指向其下一个兄弟,从而将同一父节点的所有孩子串联起来。
- 如果节点没有子节点,则左指针为空;如果没有兄弟节点,则右指针为空。
五、树与线性结构的核心区别
| 对比维度 | 树结构 | 线性结构 |
|---|---|---|
| 数据关系 | 一对多层次关系 | 一对一顺序关系 |
| 访问方式 | 从根开始导航 | 可直接索引访问 |
| 典型时间复杂度 | 查找:O(log n) | 查找:O(n) |
| 空间效率 | 可能需要更多指针空间 | 通常更紧凑 |
| 自然映射 | 组织架构、文件系统 | 任务列表、队列 |
六、二叉树
1、基本定义
- 二叉树是
每个节点最多有两个子节点的树形结构 - 子节点严格区分为
左子节点和右子节点,顺序不可互换
- 二叉树可以是空树(无任何节点)
2、特点
第 i 层最多有2^(i-1)个节点(i ≥ 1)深度为 k的二叉树最多有2^k - 1个节点叶子节点数 n₀与度为2的节点数 n₂的关系:n₀ = n₂ + 1
3、特殊二叉树类型
-
满二叉树
- 每一层节点数都达到最大值
- 深度为 k 的满二叉树有 2^k - 1 个节点
-
完全二叉树(堆)
- 除最后一层外,其余层都是满的
- 最后一层节点从左到右连续排列
- 适合用数组高效存储
-
二叉搜索树(BST)
- 左子树所有节点值 < 根节点值 < 右子树所有节点值
- 支持快速查找、插入、删除操作(平均 O(log n))
-
平衡二叉树(如AVL树、红黑树)
- 自动保持左右子树高度差在一定范围内
- 避免退化成链表,保证操作效率
4、遍历方式
- 深度优先遍历(递归/栈实现)
前序遍历:根 → 左 → 右(适合复制树结构)中序遍历:左 → 根 → 右(BST得到有序序列)后序遍历:左 → 右 → 根(适合释放内存)
- 广度优先遍历(队列实现)
层次遍历:按层从左到右访问- 适合求树的高度、宽度等
七、结语
以上是本文的全部内容,后续会有树的代码实现等内容,如有错误,感谢指正,欢迎评论区讨论!