一、先看原题:

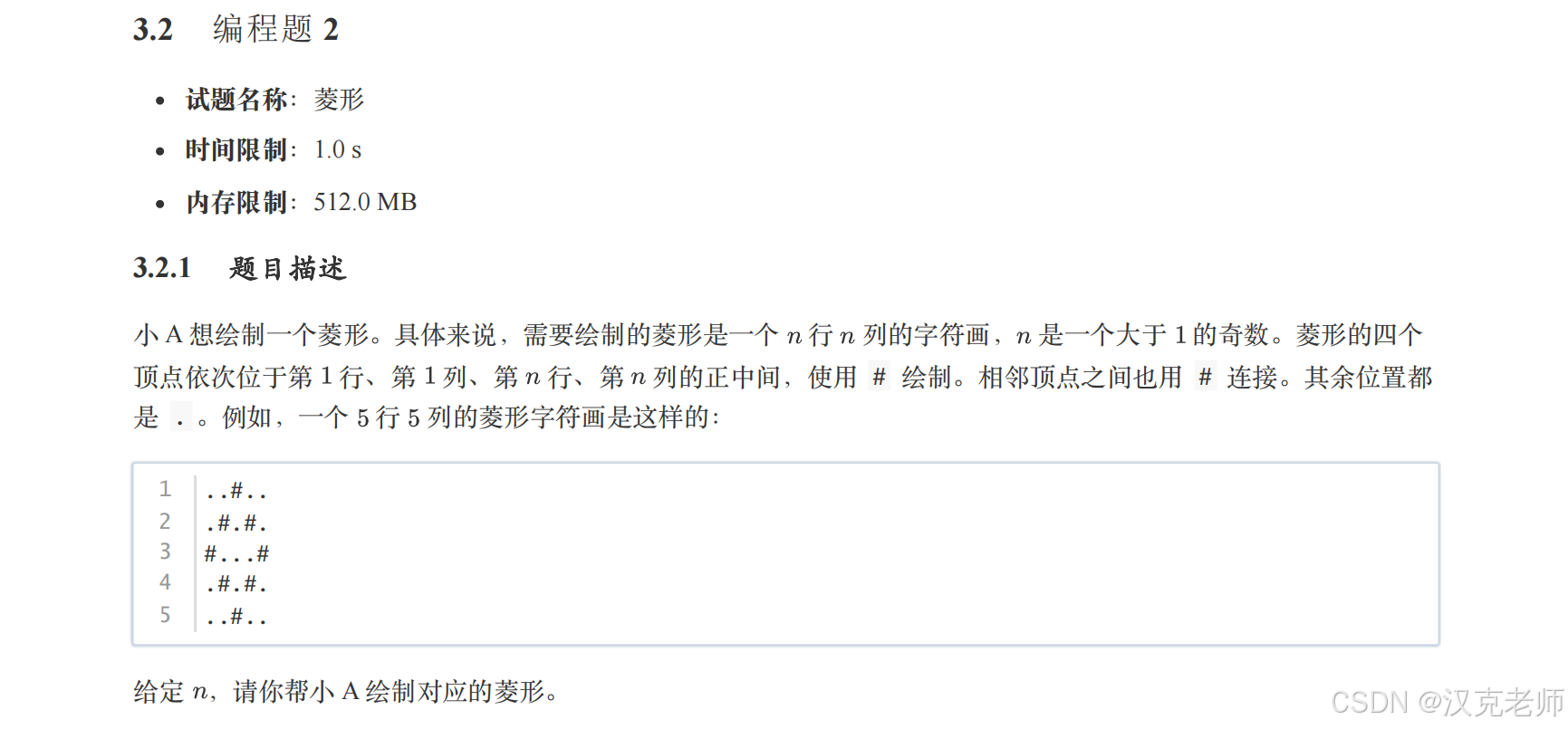


二、🎨 题目故事:小 A 要画一个菱形
1、🧸 题目故事化
小 A 学会了编程,他想用代码来画画 🖌️
这次,他要画一个 用 # 组成的菱形:
-
画布是一个 n × n 的方格
-
n是一个 大于 1 的奇数 -
不画
#的地方,用.填充
2、📌 举个例子
当 n = 5 时,要画成这样:
cpp
..#..
.#.#.
#...#
.#.#.
..#..是不是像一颗 💎 钻石?
三、🧠 这道题真正想考什么?
很多同学一看到这个图形题就慌了,其实这道题只考 3 个点:
| 考点 | 说明 |
|---|---|
| 双重 for 循环 | 一行一行画 |
| 行号 i、列号 j | 找当前位置 |
| 找"哪些点该画 #" | 核心逻辑 |
👉 最难的不是写代码,而是:判断什么时候输出 #
四、🧩 一步一步想:什么时候该画 #?
1、方法一 ⭐⭐⭐⭐
👉 发现"曼哈顿距离相等"的高明方法
这是 GESP 二级最推荐的思路
也是 从"画画"走向"数学建模" 的关键一步
1️⃣ 先讲故事
🧸 想象你站在操场正中间 🏟️
你问一个问题:
哪些格子,刚好在"菱形边界"上?
答案是:
👉 到中心点的"上下走的步数 + 左右走的步数"一样多
这就叫:
🎯 曼哈顿距离
2️⃣ 什么是"曼哈顿距离"?
在棋盘上:
-
只能 上下左右走
-
不能斜着飞 ✈️
那么:
cpp
距离 = |行差| + |列差|3️⃣ 用菱形来理解
设:
-
n = 5 -
中心在
(3, 3) -
k = n / 2 = 2
那么:
💎 所有在菱形边上的点,都满足:
cpp
|当前行 - 中心行| + |当前列 - 中心列| == 24️⃣ 举几个"一眼就懂"的例子
✅ 在菱形上
-
(1,3):|1−3| + |3−3| = 2 ✔
-
(3,1):|3−3| + |1−3| = 2 ✔
❌ 不在菱形上
-
(1,1):|1−3| + |1−3| = 4 ✘
5️⃣ 对应到代码(核心只有一行)
cpp
if (abs(i - center) + abs(j - center) == k)
'#'
else
'.'完整程序:
cpp
#include <algorithm>
#include <cstdio>
using namespace std;
int main() {
int n, i, j, k;
scanf("%d", &n);
k = n / 2; //计算半径
for (i = 1; i <= n; i++) { //枚举点的行坐标
for (j = 1; j <= n; j++) { //枚举点的列坐标
if (abs(k - i + 1) + abs(k - j + 1) == k)//计算曼哈顿距离
printf("#");
else
printf(".");
}
printf("\n"); //一行结束,转行
}
return 0;
}方法二 ⭐⭐ 没有发现刚才高明的办法怎么办?
1、👉 把菱形当成"4 条斜线"的朴素方法
这是 没有发现距离规律时 ,
非常自然、非常理性的思路
1️⃣ 先讲故事
🧸 同学看到这个菱形,会怎么想?
"它不就是
左上 → 右上 → 右下 → 左下
四条斜线拼起来的吗?"
完全正确 👍
2️⃣ 把菱形拆成 4 条边
假设 n = 5,中心是 (3,3):
四条边是:
1️⃣ 左上 ↗ 中心
2️⃣ 中心 ↘ 右上
3️⃣ 右下 ↙ 中心
4️⃣ 中心 ↖左下
3️⃣ 用数组"先画好,再统一输出"
解题思路
-
先把整个
n × n画布填成 全部都是 ' . ' -
再分别画 左上、右上、右下、左下 四条边
-
最后统一输出整个二维数组
2、分步画法:
1️⃣ 第一步:准备画布
cpp
char g[100][100];先全部填成 ' . ' :
cpp
for (i)
for (j)
g[i][j] = '.';2️⃣ 第二步:一条一条画斜线
举例:画"左上 → 中心"
cpp
int x = center, y = 1;
for (int step = 0; step <= k; step++) {
g[x][y] = '#';
x--;
y++;
}其余三条边完全类似
| 边 | 行变化 | 列变化 |
|---|---|---|
| 左上 → 中 | -1 | +1 |
| 中 → 右上 | +1 | +1 |
| 右下 → 中 | +1 | -1 |
| 中 → 左下 | -1 | -1 |
3️⃣ 最后统一输出整个数组
cpp
for (i)
for (j)
cout << g[i][j];参考程序:
cpp
#include <iostream>
using namespace std;
int main() {
int n;
cin >> n; // 输入 n(奇数)
// 画布,稍微开大一点
char g[105][105];
// 1、初始化:全部填成 '.'
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
g[i][j] = '.';
}
}
int center = (n + 1) / 2; // 中心点坐标
int k = n / 2; // 半径
// 2、 左上 -> 上中
int x = center, y = 1;
for (int step = 0; step <= k; step++) {
g[x][y] = '#';
x--;
y++;
}
// 3、上中 -> 右上
x = 1;
y = center;
for (int step = 0; step <= k; step++) {
g[x][y] = '#';
x++;
y++;
}
// 4、 右上 -> 下中
x = center;
y = n;
for (int step = 0; step <= k; step++) {
g[x][y] = '#';
x++;
y--;
}
// 5、 下中 -> 左下
x = n;
y = center;
for (int step = 0; step <= k; step++) {
g[x][y] = '#';
x--;
y--;
}
// 6、 输出整个画布
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
cout << g[i][j];
}
cout << '\n';
}
return 0;
}3、 这种朴素画图方法的特点
✅ 优点:
非常直观
像"真的在画画"
小学生很容易想到
❌ 缺点:
情况多
代码长
容易写错边界
五、两种方法的对比
| 对比项 | 方法一:曼哈顿距离 | 方法二:四条斜线 |
|---|---|---|
| 思维层次 | ⭐⭐⭐⭐ | ⭐⭐ |
| 是否发现规律 | 是 | 否 |
| 代码长度 | 短 | 长 |
| 出错概率 | 低 | 高 |
| 适合比赛 | 非常适合 | 适合 |
六、考试建议
1、👶找不到规律就用最笨的方法
👉 不怕麻烦,一条一条的写
-
建立空间感
-
理解"行、列"的变化
2、🧠 能发现规律的同学
👉 找到方法(曼哈顿距离相等)
-
从画图形 → 数学判断
-
思维直接" 升级一档 "