贪心算法
基本介绍
贪心算法是一种在每一步选择中都采取当前状态下最优策略的算法,这样在每个局部空间中可以获得局部最优解,从而可能得到全局最优解。
这种算法的每一步选择只依赖于当状态,不考虑此时的选择对未来的影响,也不回溯修正之前做的决策。问题的全局最优解可以通过一系列的局部最优解的选择来构造。总问题的最优解包含其子问题的最优解。
活动选择问题
以下所有程序均由豆包生成
cpp
#include <stdio.h>
#include <stdlib.h>
// 定义活动结构体:起始时间s,结束时间f,活动编号id
typedef struct {
int s;
int f;
int id;
} Activity;
// qsort 比较函数:按结束时间升序排序
int cmp(const void *a, const void *b) {
Activity *actA = (Activity *)a;
Activity *actB = (Activity *)b;
return actA->f - actB->f;
}
// 贪心选择活动
void selectActivities(Activity acts[], int n) {
// 1. 按结束时间排序
qsort(acts, n, sizeof(Activity), cmp);
printf("排序后的活动(按结束时间):\n");
printf("活动编号\t开始时间\t结束时间\n");
for (int i = 0; i < n; i++) {
printf("%d\t\t%d\t\t%d\n", acts[i].id, acts[i].s, acts[i].f);
}
// 2. 贪心选择:第一个活动必选
int last = 0; // 记录上一个选中活动的下标
printf("\n选中的活动编号:%d ", acts[last].id);
// 3. 遍历剩余活动,选不冲突的
for (int i = 1; i < n; i++) {
// 当前活动开始时间 >= 上一个活动结束时间 → 不冲突
if (acts[i].s >= acts[last].f) {
printf("%d ", acts[i].id);
last = i;
}
}
printf("\n");
}
int main() {
// 测试用例:5个活动,编号1~5
Activity acts[] = {
{1, 4, 1},
{3, 5, 2},
{0, 6, 3},
{5, 7, 4},
{3, 9, 5}
};
int n = sizeof(acts) / sizeof(Activity);
selectActivities(acts, n);
return 0;
}这是一个用贪心算法解决的活动选择问题,背景是:给定一组有时间重叠的活动,但是只有一个单处理器只能一个一个地处理问题,问怎样选才能选出数量最多且时间安排上不冲突的活动。
例子中的活动编号分别是1,2,3,4,5。这里算法的关键就是选结束时间最早的活动,比如活动1在第四分钟就结束了,活动1是结束最早的活动,所以先选1。这种选择的思想就用了贪心算法中的局部最优思想。接着再选在第4分钟后结束最早的活动,按照这样的逻辑最终就能得到全局最优的活动组合。
分治算法
基本介绍
其核心思想就是把复杂的问题拆成多个规模更小,结构相同的子问题,这就是"分"这一行为。由于子问题规模小,更容易解决,所以再递归解决这些子问题,这就是"治"这一行为。最后合并子问题的解得到原问题的解。
最近点距离
cpp
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <float.h>
// 定义点结构体
typedef struct Point {
double x, y;
} Point;
// 比较函数:按x坐标升序排序(qsort用)
int cmpX(const void *a, const void *b) {
Point *p1 = (Point *)a;
Point *p2 = (Point *)b;
return (p1->x - p2->x) > 0 ? 1 : -1;
}
// 比较函数:按y坐标升序排序(qsort用)
int cmpY(const void *a, const void *b) {
Point *p1 = (Point *)a;
Point *p2 = (Point *)b;
return (p1->y - p2->y) > 0 ? 1 : -1;
}
// 计算两点间的欧氏距离的平方(避免开根号,提升效率)
double distSq(Point p1, Point p2) {
return (p1.x - p2.x)*(p1.x - p2.x) + (p1.y - p2.y)*(p1.y - p2.y);
}
// 暴力求解小规模点集的最近距离(点数≤3时)
double bruteForce(Point P[], int n) {
double min = DBL_MAX;
for (int i = 0; i < n; i++) {
for (int j = i+1; j < n; j++) {
double d = distSq(P[i], P[j]);
if (d < min) min = d;
}
}
return sqrt(min);
}
// 处理跨左右区域的候选点集,返回最小距离
double stripClosest(Point strip[], int n, double d) {
double min = d;
// 按y坐标排序候选点集
qsort(strip, n, sizeof(Point), cmpY);
// 每个点最多比较后续6个点(鸽巢原理)
for (int i = 0; i < n; i++) {
for (int j = i+1; j < n && (strip[j].y - strip[i].y) < min; j++) {
double dist = sqrt(distSq(strip[i], strip[j]));
if (dist < min) min = dist;
}
}
return min;
}
// 递归分治求解最近点对距离
double closestUtil(Point P[], int n) {
// 基线条件:点数≤3,暴力求解
if (n <= 3) return bruteForce(P, n);
// 分:找中点,拆分为左右子集
int mid = n / 2;
Point midPoint = P[mid];
// 治:递归求解左右子集的最近距离
double dl = closestUtil(P, mid);
double dr = closestUtil(P + mid, n - mid);
double d = fmin(dl, dr);
// 构造跨区域候选点集strip:|x - midPoint.x| < d
Point strip[n];
int j = 0;
for (int i = 0; i < n; i++) {
if (fabs(P[i].x - midPoint.x) < d) {
strip[j++] = P[i];
}
}
// 合并:计算跨区域的最小距离,与d取最小
return fmin(d, stripClosest(strip, j, d));
}
// 主函数:统一入口
double closestPair(Point P[], int n) {
// 预处理:按x坐标排序
qsort(P, n, sizeof(Point), cmpX);
return closestUtil(P, n);
}
// 测试用例
int main() {
Point P[] = {{2, 3}, {12, 30}, {40, 50}, {5, 1}, {12, 10}, {3, 4}};
int n = sizeof(P) / sizeof(P[0]);
double minDist = closestPair(P, n);
printf("最近点对的距离为:%.4f\n", minDist);
return 0;
}问题背景是:在平面上给了一些点的坐标,问在这个平面上距离最近的一对点的距离是多少。
可以这样想,最短的距离的两个点可能都在左边,或者都在右边,或者一个在左一个在右。
这里采用了分治法,首先根据点的X轴坐标大小进行排序和拆分,找到X周的中间值点拆成左子集和右子集,然后递归计算左右子集中最近点对的距离,由于递归的拆分机制,会最终拆分到只有两个点的子集,这样再就很自然地可以进行距离计算了,每一次计算会可以认为出现了结果,一个是左子集的结果,一个是右子集的结果,再从中取最小值。这样递归结束可以找到左右子集内部的最短距离。当然最后再合并时再处理跨左右子集的最近点对就能得到最终结果了。
动态规划
基本介绍
这是一种解决多阶段决策最优解问题的算法思想,通过将复杂问题拆分成重叠子问题,并记录子问题的最优解,避免重复计算,最终推导出原问题的最优解
背包问题
cpp
#include <stdio.h>
#include <stdlib.h>
// 0-1背包二维DP实现
int knapsack01_2d(int weights[], int values[], int n, int capacity) {
// dp[i][j]:前i个物品,容量j的背包能装的最大价值
int dp[n + 1][capacity + 1];
// 初始化:0个物品或容量为0时,价值都是0
for (int i = 0; i <= n; i++) {
dp[i][0] = 0;
}
for (int j = 0; j <= capacity; j++) {
dp[0][j] = 0;
}
// 状态转移
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= capacity; j++) {
// 容量不足,无法选第i个物品(注意i从1开始,对应原数组i-1)
if (j < weights[i - 1]) {
dp[i][j] = dp[i - 1][j];
} else {
// 选与不选取最大值:不选则继承i-1的状态;选则加上当前物品价值
int not_select = dp[i - 1][j];
int select = dp[i - 1][j - weights[i - 1]] + values[i - 1];
dp[i][j] = (not_select > select) ? not_select : select;
}
}
}
return dp[n][capacity];
}
int main() {
// 测试用例:物品重量、价值、数量、背包容量
int weights[] = {2, 3, 4, 5}; // 4个物品的重量
int values[] = {3, 4, 5, 6}; // 对应价值
int n = sizeof(weights) / sizeof(weights[0]);
int capacity = 8; // 背包容量
int max_value = knapsack01_2d(weights, values, n, capacity);
printf("二维DP版最大价值:%d\n", max_value);
return 0;
}问题背景:给定一个容量为C的背包,现有n个物品,每个物品有重量和价值这两个熟悉,每个物品只能选一次,先要找出一个使得背包不超重的情况下,总价值最大的物品选择方案。
本算法中首先定义dp[i][j]这种状态,其表示前i个物品,装入容量为j的背包能获得的最大价值。然后两个for循环遍历i和j的所有情况。每一次循环都是一个新的状态,可以有选和不选第i个物品的决策。最终得到以下这张表: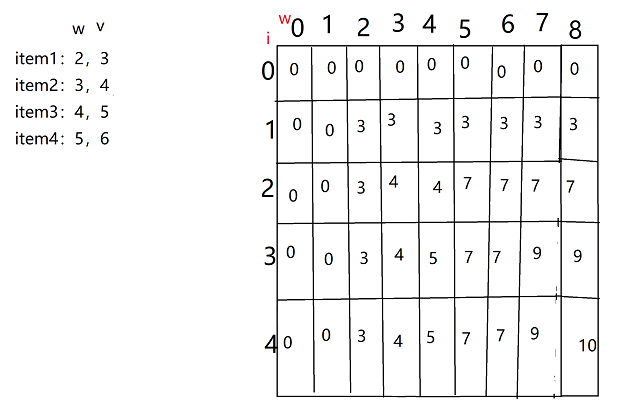
最后的10就是最大的总价值。
随机化算法
基本介绍
指的是在算法中引入随机数来决定下一步的操作,一般用于获得大概率下的结果。
素性测试
cpp
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <stdbool.h>
// 快速幂取模:(base^exponent) % mod,防止溢出
long long mod_pow(long long base, long long exponent, long long mod) {
long long result = 1;
base %= mod;
while (exponent > 0) {
if (exponent % 2 == 1) {
result = (result * base) % mod;
}
base = (base * base) % mod;
exponent /= 2;
}
return result;
}
// Miller-Rabin单次测试
bool miller_rabin_test(long long n, long long a) {
if (n <= 1) return false;
if (n == 2 || n == 3) return true;
if (n % 2 == 0) return false;
long long d = n - 1;
int s = 0;
// 分解 n-1 = d*2^s
while (d % 2 == 0) {
d /= 2;
s++;
}
long long x = mod_pow(a, d, n);
if (x == 1 || x == n - 1) return true;
for (int i = 0; i < s - 1; i++) {
x = mod_pow(x, 2, n);
if (x == n - 1) return true;
}
return false;
}
// 多次测试提高准确性,k为测试次数
bool is_prime(long long n, int k) {
if (n <= 1) return false;
if (n == 2 || n == 3) return true;
if (n % 2 == 0) return false;
srand((unsigned int)time(NULL));
for (int i = 0; i < k; i++) {
// 随机选取底数 a ∈ [2, n-2]
long long a = 2 + rand() % (n - 3);
if (!miller_rabin_test(n, a)) {
return false;
}
}
return true;
}
// 测试用例
int main() {
long long n;
int k = 5; // 测试5次,次数越多越准确
printf("请输入需要测试的整数: ");
scanf("%lld", &n);
if (is_prime(n, k)) {
printf("%lld 大概率是素数\n", n);
} else {
printf("%lld 是合数\n", n);
}
return 0;
}如果要快速判断一个大数是否是素数的话,可以用随机的思想,其做法是先随机生成一些数,如果这个大数不能整除这些数的话,那大概率可以认为这个大数是素数。
回溯算法
基本介绍
其核心是尝试-验证-回退:在解决多阶段决策问题上,逐步构建解的途径,每一步选择一个可能的选项,如果当前路径无法得到有效解的话,那就回退到上一步再尝试其他选择,直到找到有效解。
数独求解
cpp
#include <stdio.h>
#include <stdbool.h>
#define SIZE 9
// 检查在 (row, col) 位置填入 num 是否合法
bool isSafe(int board[SIZE][SIZE], int row, int col, int num) {
// 1. 检查当前行是否有重复
for (int i = 0; i < SIZE; i++) {
if (board[row][i] == num) {
return false;
}
}
// 2. 检查当前列是否有重复
for (int i = 0; i < SIZE; i++) {
if (board[i][col] == num) {
return false;
}
}
// 3. 检查 3x3 子宫格是否有重复
int startRow = row - row % 3; // 子宫格起始行
int startCol = col - col % 3; // 子宫格起始列
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
if (board[startRow + i][startCol + j] == num) {
return false;
}
}
}
return true;
}
// 寻找棋盘上的第一个空格,找到则将 row、col 赋值并返回 true
bool findEmptyCell(int board[SIZE][SIZE], int *row, int *col) {
for (*row = 0; *row < SIZE; (*row)++) {
for (*col = 0; *col < SIZE; (*col)++) {
if (board[*row][*col] == 0) {
return true;
}
}
}
return false; // 无空格,数独已解
}
// 回溯法求解数独
bool solveSudoku(int board[SIZE][SIZE]) {
int row, col;
// 终止条件:没有空格,求解成功
if (!findEmptyCell(board, &row, &col)) {
return true;
}
// 尝试填入 1-9
for (int num = 1; num <= SIZE; num++) {
if (isSafe(board, row, col, num)) {
board[row][col] = num; // 暂时填入
// 递归求解后续空格
if (solveSudoku(board)) {
return true;
}
// 回溯:当前数字导致后续无解,重置为空格
board[row][col] = 0;
}
}
return false; // 所有数字都尝试过,无解
}
// 打印数独棋盘
void printBoard(int board[SIZE][SIZE]) {
for (int row = 0; row < SIZE; row++) {
for (int col = 0; col < SIZE; col++) {
printf("%d ", board[row][col]);
}
printf("\n");
}
}
// 测试用例
int main() {
// 0 表示空格
int board[SIZE][SIZE] = {
{5, 3, 0, 0, 7, 0, 0, 0, 0},
{6, 0, 0, 1, 9, 5, 0, 0, 0},
{0, 9, 8, 0, 0, 0, 0, 6, 0},
{8, 0, 0, 0, 6, 0, 0, 0, 3},
{4, 0, 0, 8, 0, 3, 0, 0, 1},
{7, 0, 0, 0, 2, 0, 0, 0, 6},
{0, 6, 0, 0, 0, 0, 2, 0, 0},
{0, 0, 0, 4, 1, 9, 0, 0, 5},
{0, 0, 0, 0, 8, 0, 0, 7, 9}
};
printf("原始数独:\n");
printBoard(board);
if (solveSudoku(board)) {
printf("\n求解后的数独:\n");
printBoard(board);
} else {
printf("\n该数独无解!\n");
}
return 0;
}数独的规则是:在9×9的棋盘上,每列每行的数字都是1-9不重复,部分格子已预先填充。
回溯算法的逻辑是,在未填充的格子上随机填数字,每填一次就检查是否合法,如果合法的话就找下一个空格随机填数,如果检查出不合法的话就让当前格子的数重置再试下一个数字,直到填完最后一个空格且合法。