树的概念及结构
1.1 树的概念
树 (Tree)是一种非线性的数据结构 ,它是由 n ((( n \\geq 0 )个有限结点组成的一个具有层次关系的集合。
- 把它叫做"树",是因为其结构形似一棵倒挂的树 :根朝上,叶朝下。
- 根结点 (Root):树中一个特殊的结点,没有前驱结点。
- 除根结点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、......、Tm,其中每一个集合Ti(1<= i <= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继
- 每棵子树的根结点有且只有一个前驱 (即父结点),但可以有 0 个或多个后继(即子结点)。
树是递归定义的 。
注意:树形结构中,任意两棵子树之间不能有交集,否则就不是树。
1.2 树的相关概念
| 术语 | 定义 | 示例(假设图中根为 A) |
|---|---|---|
| 结点的度 | 一个结点所含子树的个数 | A 的度为 6 |
| 叶结点 / 终端结点 | 度为 0 的结点 | B、C、H、I 等 |
| 非终端结点 / 分支结点 | 度不为 0 的结点 | D、E、F、G 等 |
| 父结点 / 双亲结点 | 若结点 X 有子结点 Y,则 X 是 Y 的父结点 | A 是 B 的父结点 |
| 子结点 / 孩子结点 | 若结点 X 有子树,其根即为 X 的子结点 | B 是 A 的孩子结点 |
| 兄弟结点 | 具有相同父结点的结点互为兄弟 | B 和 C 是兄弟结点 |
| 树的度 | 树中所有结点的度的最大值 | 树的度为 6 |
| 结点的层次 | 从根开始定义:根为第 1 层 ,其子为第 2 层,依此类推 | A:1层,B/C:2层,...... |
| 树的高度 / 深度 | 树中结点的最大层次数 | 高度为 4 |
| 堂兄弟结点 | 父结点在同一层的结点互为堂兄弟 | H 和 I 的父结点(如 E 和 F)若在同一层,则 H 与 I 为堂兄弟 |
| 祖先 | 从根到该结点路径上的所有结点 | A 是所有结点的祖先 |
| 子孙 | 以某结点为根的子树中的所有结点 | 所有结点都是 A 的子孙 |
| 森林 | 由 m ((( m \> 0 )棵互不相交的树组成的集合 | 多棵树 ⇒ 森林 |
注:
- "堂兄弟"强调的是父结点处于同一层,而非是否相邻;
- 森林可看作是"去掉了根结点的树"------一棵树去掉根后,其各子树构成森林。
- 树的度与离散数学中图的度有一定区别
1.3 树的表示
树结构比线性表更复杂,不仅要存储结点的数据(值域) ,还要保存结点之间的层次与关联关系 。
因此,树有多种存储表示方法,常见的包括:
- 双亲表示法:每个结点记录其父结点的位置;
- 孩子表示法:每个结点记录其所有子结点;
- 孩子双亲表示法:同时记录父结点和子结点;
- 孩子兄弟表示法 (二叉树表示法):每个结点只记录第一个孩子 和下一个兄弟。
在实际应用中,孩子兄弟表示法最为常用,尤其在将普通树转化为二叉树进行处理时非常高效。
孩子兄弟表示法(Left-Child Right-Sibling Representation)
核心思想:
将任意一棵树 转换为二叉树形式表示:
- 每个结点有两个指针:
firstChild(或left):指向第一个孩子;nextSibling(或right):指向紧邻的下一个兄弟。
结点结构定义(C语言示例):
c
typedef int DataType;
typedef struct TreeNode {
DataType data; // 结点数据
struct TreeNode* firstChild; // 指向第一个孩子
struct TreeNode* nextBrother; // 指向下一个兄弟
} TreeNode;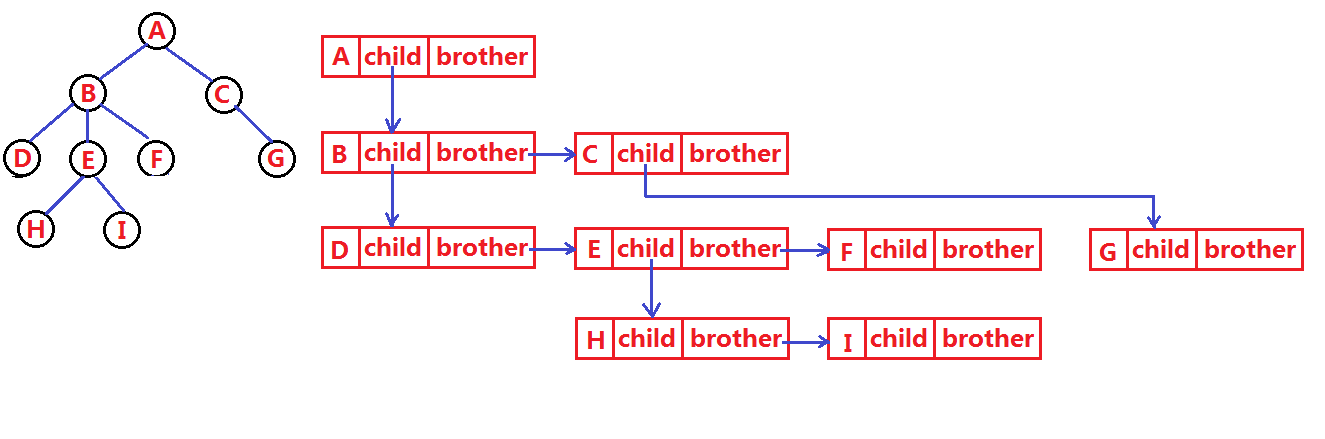
如图,使用孩子指针储存子节点,兄弟指针储存同级节点,实现树状存储。
二叉树概念及结构
2.1 二叉树的概念
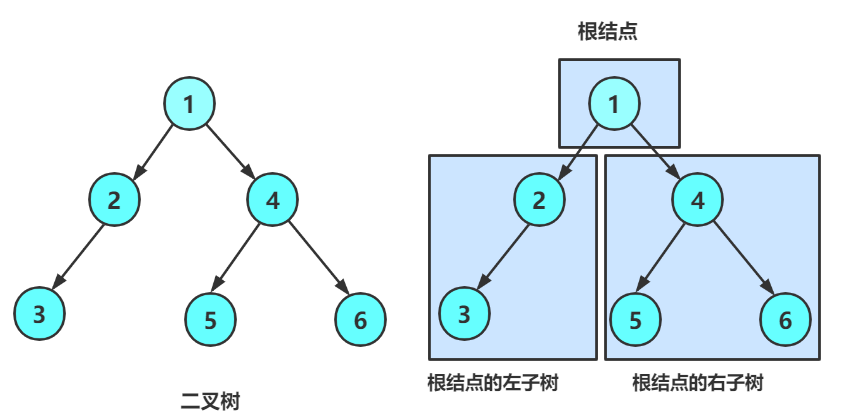
一棵二叉树 (Binary Tree)是结点的一个有限集合,该集合满足以下两个条件之一:
- 空集合(即空树);
- 由一个根结点 (root),其中:
- 左子树和右子树本身也是二叉树;
- 左、右子树有严格顺序之分 ,即使某子树为空,其位置仍有意义。
关键特性:
- 每个结点最多有两个子结点;
- 子结点分为左孩子 (left child)和右孩子 (right child),顺序不可交换 。
(例如:左子树为空、右子树非空 ≠ 右子树为空、左子树非空)
2.3 特殊的二叉树
1. 满二叉树(Full Binary Tree / Perfect Binary Tree)
-
定义 :一棵深度为 K 的二叉树,如果每一层的结点数都达到最大值,则称为满二叉树。
-
第 i 层最多有 2^(i-1) 个结点(根为第 1 层);
-
深度为 K 的满二叉树的总结点数为:
n = 2^K - 1
-
特点:
- 所有叶子结点都在最底层;
- 除叶子外,每个非叶结点都有两个孩子;
- 结构完全对称、紧凑。
2. 完全二叉树(Complete Binary Tree)
-
定义 :对于深度为k节点数数是 n个结点的二叉树,若其每个结点的位置都与深度为 K 的满二叉树中编号从 1 到 n 的结点一一对应,则称为完全二叉树。
- 编号按层序遍历(从上到下、从左到右)进行。
-
直观理解:
- 除最后一层外,其他层都是满的;
- 最后一层的结点全部靠左排列,不能有"空洞"。
-
关键性质:
- 叶子结点只可能出现在最后两层;
- 若存在度为 1 的结点,则只能有一个 ,且是左孩子;
- 满二叉树是完全二叉树的特例(当 n = 2^K - 1 时)。
-
为什么重要?
- 完全二叉树可以高效地用数组存储(无空间浪费);
- 是堆(Heap)等高效数据结构的基础;
- 支持 O(1) 时间通过下标计算父子关系。
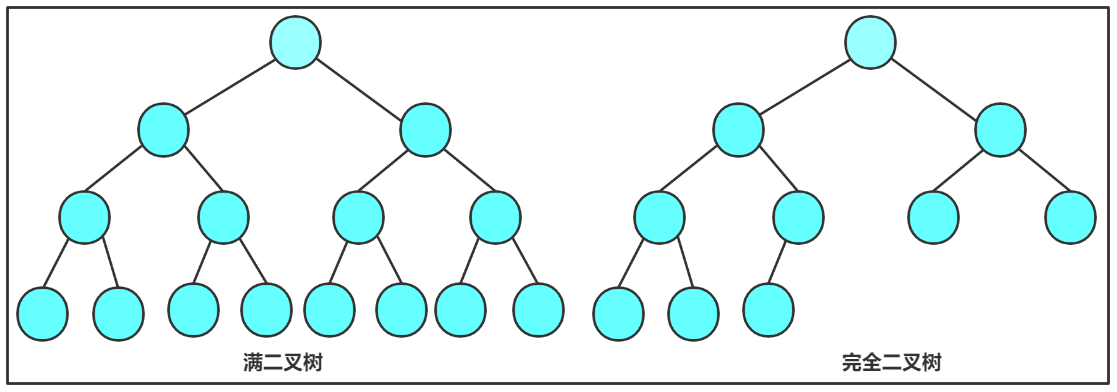
满二叉树 vs 完全二叉树 对比
| 特性 | 满二叉树 | 完全二叉树 |
|---|---|---|
| 是否每层都满? | 是 | 最后一层可不满 |
| 最后一层是否靠左? | ---(已满) | 必须靠左 |
| 是否一定是完全二叉树? | 是 | 不一定(如右偏树就不是) |
| 能否用数组高效存储? | 能 | 能(且更通用) |
2.5 二叉树的存储结构
二叉树的存储方式主要有两种:顺序存储 和 链式存储。它们各有适用场景和优缺点。
1. 顺序存储(数组实现)
- 实现方式 :使用数组 按层序遍历的顺序存储结点。
- 适用条件 :仅适合完全二叉树 (或接近完全的二叉树)。
- 原因:非完全二叉树在数组中会产生大量空洞 (用无效值如
null填充),造成空间浪费。
- 原因:非完全二叉树在数组中会产生大量空洞 (用无效值如
- 父子关系通过下标计算 (根结点位于下标 0):
- 父结点:
parent = (i - 1) / 2 - 左孩子:
left = 2 * i + 1 - 右孩子:
right = 2 * i + 2
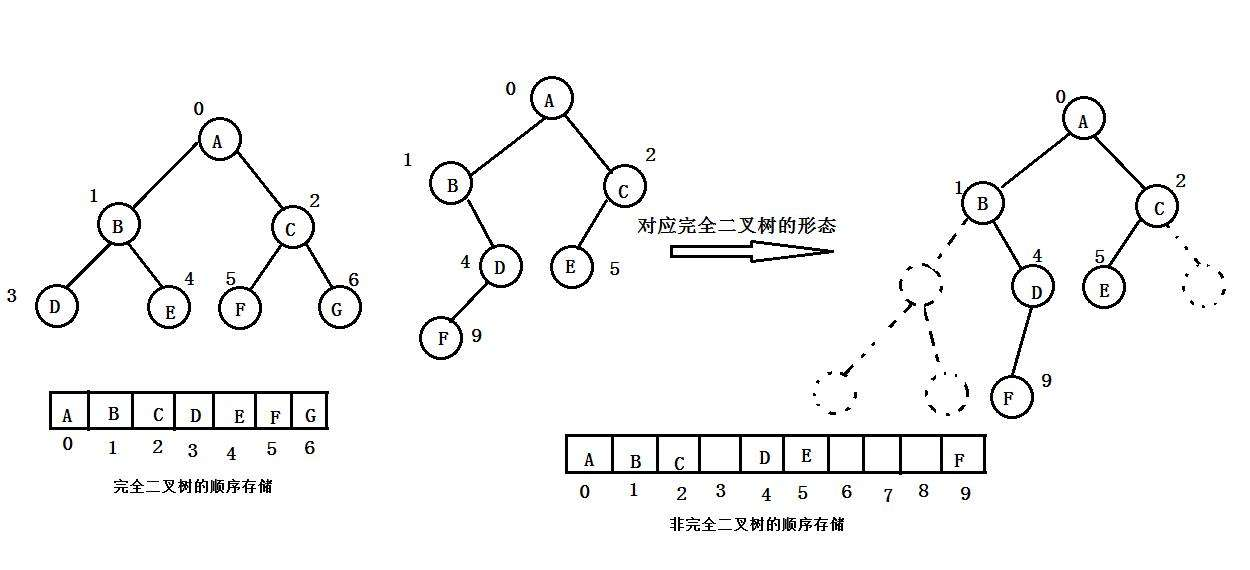
- 父结点:
对于非完全二叉树,也可以使用数组顺序储存,但是需要补齐空的子节点,会造成大量空间浪费
典型应用 :堆 (Heap)------因其本质是完全二叉树,故广泛采用数组顺序存储。
一般二叉树不推荐使用顺序存储。
- 特点 :
- 物理结构:连续的数组;
- 逻辑结构:仍是一棵二叉树;
- 优点:空间紧凑(对完全二叉树)、缓存友好、支持 O(1) 随机访问;
- 缺点:对普通二叉树空间效率极低。
2. 链式存储(指针/引用实现)
- 实现方式 :使用链表结构 ,每个结点包含:
- 数据域(存储结点值);
- 左指针域(指向左孩子);
- 右指针域(指向右孩子)。
c
typedef struct BinaryTreeNode {
DataType data;
struct BinaryTreeNode* left; // 指向左子树
struct BinaryTreeNode* right; // 指向右子树
} BTNode;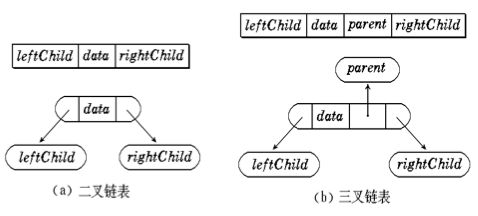
优点:结构简单,适用于绝大多数二叉树操作(遍历、构建、删除等);
应用场景:二叉搜索树(BST)、普通二叉树、表达式树等。