本文记录使用张氏标定法进行使用的全过程，并记录最终的误差成果,为什么需要标定是因为相机本身拍照之后，就存在一个畸变，所以仅靠一个比例尺来进行推算实际距离和像素距离之间的比例，是存在很大的偏差的，理解一下，拍完照就存在了，后面你怎么计算都会存在问题。以及标定结束之后，相机是固定的，一旦相机移动，或者焦距发生改变，就需要重新进行标定，而且标定之后，同样只是在一个平面内进行比例尺的测算才会准确，一旦，物体变为三维，到相机镜头的工作距离发生改变，那么计算之后的误差同样会变大。

1.首先需要找到对应的实验器材

硬件：相机机架，相机，直尺，以及标定板（可以自己制作）

软件：能够实现相机拍照，自己使用SDK进行二次开发，能够使用开源的opnecv 库进行计算对应的校正值，在新的程序中c++中进行使用。

2.实验步骤：

2.1.制作标定板，先去相机校准图案生成器 -- calib.io ，生成对应的标定PDF，如下图

上述为本人使用的样式，然后打印为A4纸张。但是最终实际测量一个小方格的边长为13mm。需要根据实际测算的边长进行更改。然后方格数量为8 * 11 ，由此可知，角点数量为7 * 10,（角点就是实际上的两个方块相交的点）。然后将标定板固定到一个完全平滑的板子上。

2.1.拍照，在相机固定固定之后，接下来需要拍摄几张十分干净，标准的照片进行标定。特点如下

标定板清晰无模糊

角度覆盖充分但不过度

相机固定不动，最好是10张以上。

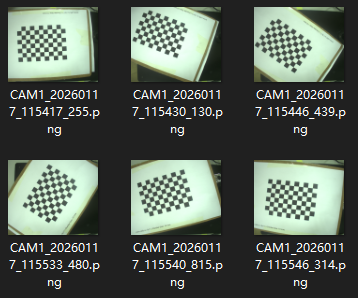
2.1.然后就是使用vs code，使用python语言来进行标定脚本的书写，运行程序，得出对应的标定结果。脚本如下，此处不在赘述，怎么去配置环境，等等

python 复制代码

import numpy as np
import cv2
import glob

# 1. 准备标定板参数
chessboard_size = (7, 10)  # 内角点数量
square_size = 13.0  # 毫米

# 2. 生成世界坐标系中的3D点
objp = np.zeros((chessboard_size[0]*chessboard_size[1], 3), np.float32)
objp[:, :2] = np.mgrid[0:chessboard_size[0], 
                       0:chessboard_size[1]].T.reshape(-1, 2) * square_size

# 3. 存储对象点和图像点
objpoints = []  # 3D点
imgpoints = []  # 2D点

# 4. 读取所有标定图像
images = glob.glob('D:/DeepLearning/datasets/clibration/rect/*.png')
image_size = None

for fname in images:
    img = cv2.imread(fname)
    gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
    
    if image_size is None:
        image_size = gray.shape[::-1]
    
    # 查找棋盘格角点
    ret, corners = cv2.findChessboardCorners(gray, chessboard_size, None)
    
    if ret:
        objpoints.append(objp)
        
        # 亚像素精确化
        corners2 = cv2.cornerSubPix(gray, corners, (11,11), (-1,-1),
                                   (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 30, 0.001))
        imgpoints.append(corners2)
        
        # 可视化角点
        cv2.drawChessboardCorners(img, chessboard_size, corners2, ret)
        cv2.imshow('Corners', img)
        cv2.imwrite("this.png",img)
        cv2.waitKey(500)

cv2.destroyAllWindows()

# 5. 相机标定
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(objpoints, imgpoints, 
                                                   image_size, None, None)

print("相机内参矩阵:\n", mtx)
print("\n畸变系数:", dist.ravel())

# 6. 评估标定误差
mean_error = 0
for i in range(len(objpoints)):
    imgpoints2, _ = cv2.projectPoints(objpoints[i], rvecs[i], tvecs[i], mtx, dist)
    error = cv2.norm(imgpoints[i], imgpoints2, cv2.NORM_L2)/len(imgpoints2)
    mean_error += error

print("\n平均重投影误差: {} 像素".format(mean_error/len(objpoints)))

# 7. 保存标定结果
np.savez('calibration_result.npz', mtx=mtx, dist=dist)

注意，其中参数的改写，以及对应的路径的变更

1. 准备标定板参数

chessboard_size = (7, 10) # 内角点数量

square_size = 13.0 # 毫米

以及文件路径。

2.2.运行得到结果如下

相机内参矩阵:

\[2.78225009e+03 0.00000000e+00 1.20301433e+03

0.00000000e+00 2.77841102e+03 1.00512050e+03

0.00000000e+00 0.00000000e+00 1.00000000e+00\]

畸变系数: [-0.2517598 0.07004305 -0.00127046 0.00606034 0.24205241]

平均重投影误差: 0.07069074329111907 像素

由此可知，标定结果还可以，主要看重投影误差，为0.07，当然其他参数一会同样需要使用。

2.3.将参数使用到对相机拍摄的照片进行校正，需要会SDK取图，并且取图之后，能够进行处理，如下，为拍摄照片之后的处理代码。

cpp 复制代码

cv::Mat CFormal_DecDlg::FastUndistort(const cv::Mat& input)
{
	static cv::Mat cameraMatrix = (cv::Mat_<double>(3, 3) <<
		2782.25009, 0.0, 1203.01433,
		0.0, 2778.41102, 1005.1205,
		0.0, 0.0, 1.0);

	static cv::Mat distCoeffs = (cv::Mat_<double>(1, 5) <<
		-0.2517598, 2.77841102, 0.00127046,
		0.00606034, -0.24205241);

	static cv::Mat map1, map2;
	static cv::Size lastSize(0, 0);

	// 如果尺寸变化或第一次，计算映射
	if (map1.empty() || input.size() != lastSize) {
		cv::Mat newCameraMatrix = cv::getOptimalNewCameraMatrix(
			cameraMatrix, distCoeffs, input.size(), 1.0, input.size()
		);

		cv::initUndistortRectifyMap(
			cameraMatrix, distCoeffs, cv::Mat(),
			newCameraMatrix, input.size(),
			CV_32FC1, map1, map2
		);
		lastSize = input.size();
	}

	cv::Mat result;
	cv::remap(input, result, map1, map2, cv::INTER_LINEAR);
	return result;
}

，对图像进行处理之后，会得到下述样式的图像，即校正之后的图像。

，本人随机取出中间的两个点(590,1069) （718.1074），进过转换如下

首先，提取并整理你的相机参数：

相机内参矩阵 (K):

text

复制代码

fx = 2782.25009  # 图像x轴方向焦距
fy = 2778.41102  # 图像y轴方向焦距
cx = 1203.01433  # 图像主点坐标x
cy = 1005.12050  # 图像主点坐标y

畸变系数 (D) : [-0.2517598, 0.07004305, -0.00127046, 0.00606034, 0.24205241]
工作距离 (Z): 285 mm
图像点:
- 点 A: (590, 1069)
- 点 B: (718, 1074)

计算步骤如下：

校正畸变：由于畸变会改变像素点的理想位置，计算前需先去除畸变影响。
- 点 A 校正后: (588.31, 1068.75)
- 点 B 校正后: (716.08, 1073.85)
像素坐标转归一化相机坐标 ：

公式为：
X_normal = (x_corrected - cx) / fx
Y_normal = (y_corrected - cy) / fy
- 点 A 归一化坐标: (-0.2209, 0.0229)
- 点 B 归一化坐标: (-0.1751, 0.0247)
归一化坐标转实际三维坐标 ：

已知实际工作距离（Z = 285 mm），通过相似三角形计算：
X_real = X_normal * Z
Y_real = Y_normal * Z
- 点 A 实际坐标: (-62.95 mm, 6.53 mm, 285.00 mm)
- 点 B 实际坐标: (-49.89 mm, 7.05 mm, 285.00 mm)
计算三维空间距离 ：

利用三维空间两点间距离公式计算：
最终距离 D = √((X_B - X_A)² + (Y_B - Y_A)² + (Z_B - Z_A)²) = 13.09 mm

结果为13.09，即实际距离为13.09，是校正之后，进行计算的结果。跟13mm十分的接近，说明标定方法是可以的。

除开上述的反投影法计算实际距离之外，还存在另外的方法，计算比例尺

原理：在焦距 f (像素) 和工作距离 Z (毫米) 已知时，图像传感器上一个像素对应的实际尺寸是固定的。
计算：比例尺 S (毫米/像素) = Z / f。
- 在X方向：S_x = Z / fx = 285 / 2782.25009 ≈ 0.10245 mm/像素
- 在Y方向：S_y = Z / fy = 285 / 2778.41102 ≈ 0.10256 mm/像素
距离：两点像素坐标差 Δx = 718 - 590 = 128 像素， Δy = 1074 - 1069 = 5 像素。
实际距离 ：D = √((Δx * S_x)² + (Δy * S_y)²) = √((128*0.10245)² + (5*0.10256)²) ≈ √(172.14 + 0.263) ≈ √172.40 ≈ 13.13 mm。

同样误差很小，一般可以投入实际使用。

张氏相机标定，不求甚解使用篇

1. 准备标定板参数