为何要研究直线沿本身的伸缩变换?
黄小宁
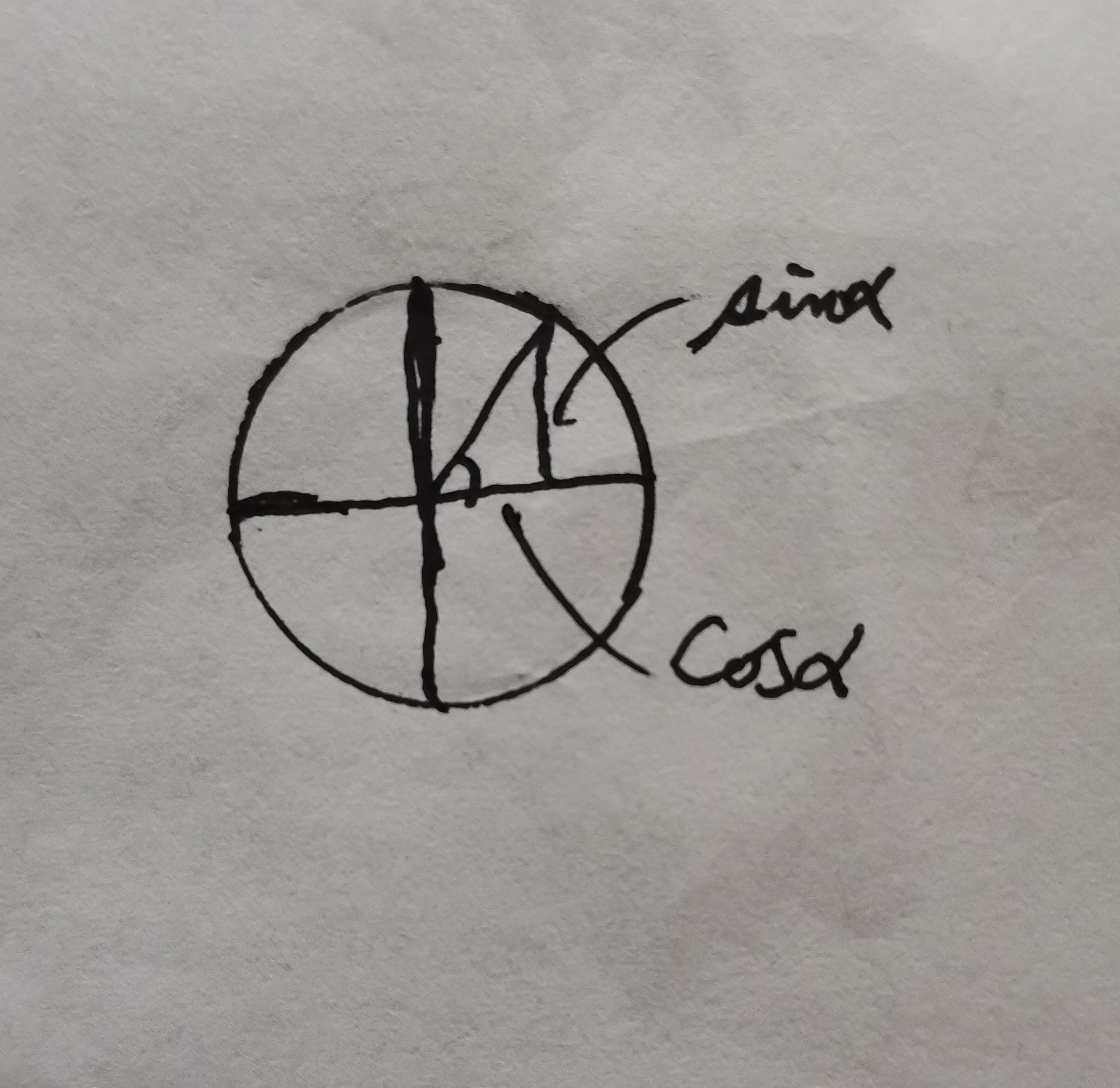
如草图所示初等数学中的单位圆内的直角三角形的直角边(直线段)随着斜边绕圆心的旋转而作伸长、缩短变换------说明直线段有伸长和缩短变换;而直线段是直线的一部分,所以须研究直线沿本身的伸缩变换。
2300年直线公理使数学有几百年函数"常识":直线沿本身的伸缩变换是变回自己的变换。本人发现这是将无穷多各异直线误为同一线的"井底蛙"误区。将两异直线误为同一线自然就会将两异直线段误为同一线段(初等数学有几百年函数"常识":直线段a均匀缩短成直线段b~a中的b必是a的一部分)从而使康脱推出错上加错的更重大错误:直线段的部分点可与全部点一样多。