（论文速读）GNS：学习用图网络模拟复杂物理

****论文题目：****Learning to Simulate Complex Physics with Graph Networks（学习用图网络模拟复杂物理）

会议：ICML2020

****摘要：****在这里，我们提出了一个机器学习框架和模型实现，可以学习模拟各种具有挑战性的物理领域，包括流体、刚性固体和相互作用的可变形材料。我们的框架------我们称之为"基于图形网络的模拟器"(GNS)------用粒子表示物理系统的状态，用图形中的节点表示，并通过学习的消息传递来计算动态。我们的结果表明，我们的模型可以从训练期间具有数千个粒子的单时间步预测推广到不同的初始条件，数千个时间步，并且在测试时至少有一个数量级的粒子。我们的模型对各种评估指标的超参数选择具有鲁棒的:长期性能的主要决定因素是消息传递步骤的数量，以及通过用噪声破坏训练数据来减轻错误的积累。我们的GNS框架推进了最先进的学习物理模拟，并有望解决各种复杂的正演和逆问题。

用图神经网络学习复杂物理仿真：DeepMind的GNS框架深度解读

引言

物理仿真在科学研究和工程应用中扮演着至关重要的角色。然而，传统的物理模拟器开发周期长、计算成本高，且难以在准确性和通用性之间取得平衡。DeepMind在ICML 2020上发表的这篇论文提出了一个突破性的解决方案------Graph Network-based Simulators (GNS)，通过机器学习直接从数据中学习物理仿真。

这篇博客将详细解读这项工作的核心思想、技术细节和实验结果。

一、研究背景与动机

复制代码

# 初始状态：100个水粒子在空中
for 每一步 in range(1000):
    # 1. 构建图（邻居关系会变化）
    图 = 连接距离<R的粒子对
    
    # 2. 编码器
    节点特征 = MLP([过去5步速度, 材料="水"])
    边特征 = MLP([相对位移, 距离])
    
    # 3. 10次消息传递（核心计算）
    for i in range(10):
        传递信息()
        更新节点特征()
    
    # 4. 解码器
    加速度 = MLP(最终节点特征)
    
    # 5. 物理更新
    速度 += 加速度 × Δt
    位置 += 速度 × Δt

1.1 传统物理仿真的局限性

传统物理仿真器面临以下挑战：

开发成本高：构建一个高质量仿真器往往需要数年的工程努力
通用性受限：为了在特定场景下保证准确性，通常需要牺牲通用性
计算开销大：高精度仿真需要大量计算资源，难以大规模应用
近似误差：由于对底层物理的认识不足或近似困难，即使最好的仿真器也存在误差

1.2 机器学习方法的困境

虽然从数据中学习仿真器是一个诱人的替代方案，但标准的端到端学习方法难以克服以下障碍：

物理系统的状态空间巨大
动力学过程高度复杂
长期预测中的误差累积问题

二、GNS框架核心思想

2.1 基本理念

GNS框架的核心理念是将物理仿真问题转化为图上的消息传递问题：

节点：代表物理系统中的粒子
边：代表粒子间的潜在交互关系
消息传递：通过学习的函数模拟粒子间的相互作用

这种表示方式具有强归纳偏置（inductive bias），与基于粒子的物理仿真方法（如SPH、PBD、MPM）天然契合。

2.2 整体架构

GNS采用"编码器-处理器-解码器"（Encode-Process-Decode）架构：

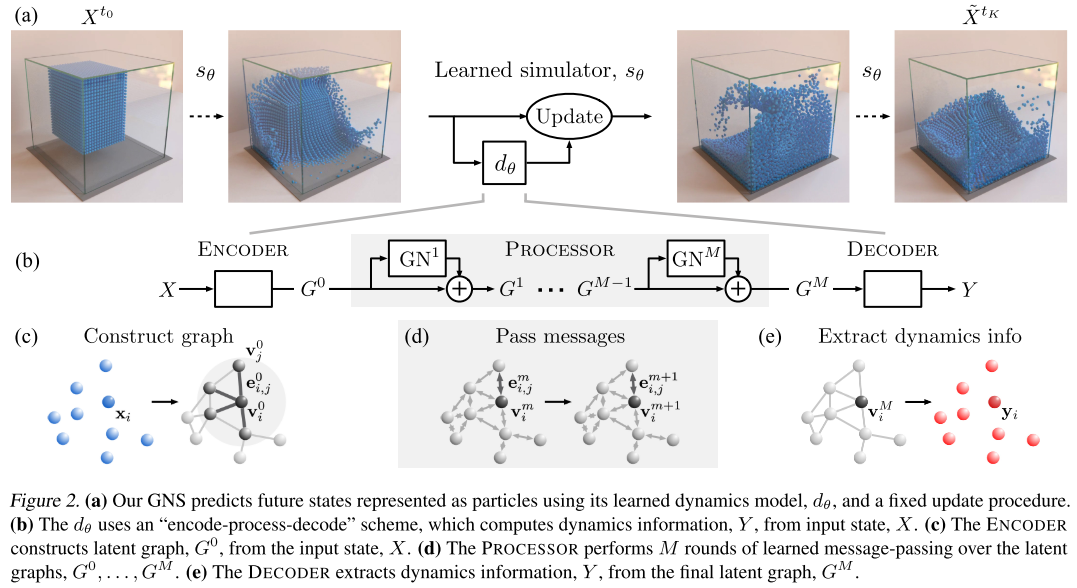
编码器（Encoder）

编码器的任务是将粒子状态转换为图结构：

节点特征：每个粒子的输入状态包括：
- 当前位置
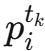
- 最近C=5个时间步的速度历史
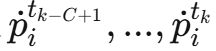
- 静态材料属性（水、沙、goop、刚体、边界）
边的构建：在"连接半径"R内的粒子对之间添加有向边
两种编码变体：
- 绝对编码：直接使用粒子的绝对位置
- 相对编码 ：使用粒子间的相对位移

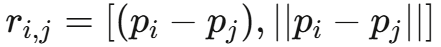
实验表明，相对编码由于引入了空间平移不变性，性能明显优于绝对编码。

处理器（Processor）

处理器通过M步消息传递计算粒子间的交互：

其中：

每一步都是一个图神经网络（GN）
使用多层感知机（MLP）作为边和节点的更新函数
采用残差连接提高训练稳定性

关键发现：消息传递步数M是影响性能的最重要因素之一，更多的步数允许计算更长距离和更复杂的交互。

解码器（Decoder）

解码器从最终的图状态中提取动力学信息：

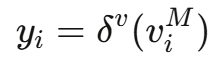
这里yi代表粒子的加速度，然后通过欧拉积分器更新位置和速度：

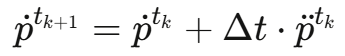
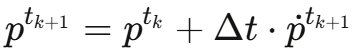
2.3 关键技术细节

2.3.1 训练噪声

为了使模型对噪声输入更加鲁棒，训练时对输入速度添加随机游走噪声：

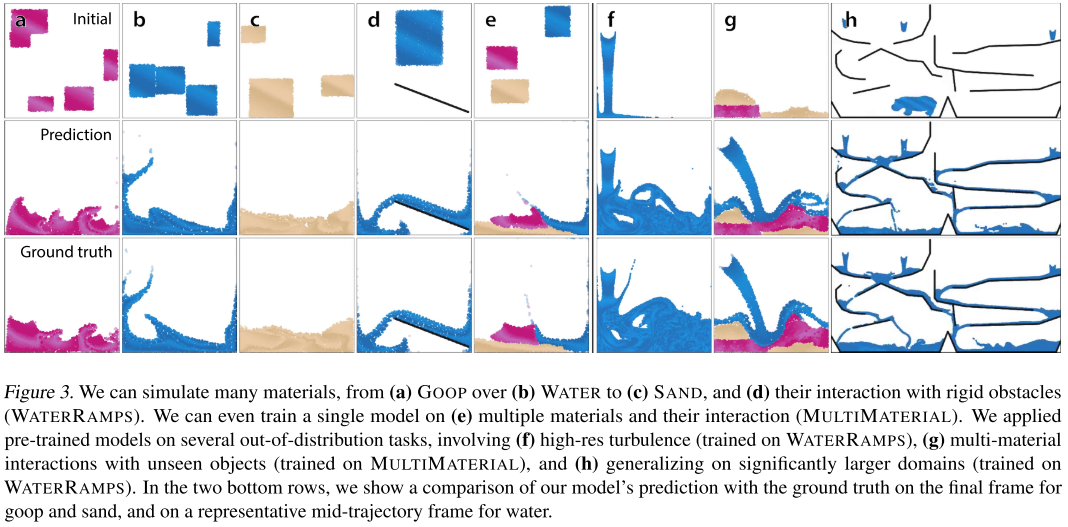
这模拟了长期预测中的误差累积，使模型在推理时能更好地处理自身预测产生的噪声。（观察图中的g图和h图）

2.3.2 归一化

所有输入和目标向量都被归一化为零均值和单位方差，使用训练过程中在线计算的统计量。这加速了训练过程，但对最终收敛性能影响不大。

2.3.3 损失函数

使用单步预测的L2损失：

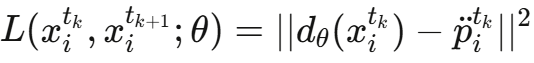
优化器采用Adam，学习率从10^-4指数衰减到10^-6，最多训练20M步。

三、实验设置

3.1 物理域

论文在17个不同的数据集上进行了实验，涵盖：

流体：WATER-3D（SPH模拟）、BOXBATH（PBD模拟）
颗粒材料：SAND（摩擦行为复杂）
可变形材料：GOOP（粘塑性材料）
多材料交互：MULTIMATERIAL（水、沙、goop同时存在）
复杂场景：WATERRAMPS（水流过1-5个障碍物）、FLUIDSHAKE（容器剧烈晃动）

每个数据集通常包含：

1000个训练轨迹
100个验证轨迹
100个测试轨迹
每条轨迹300-2000个时间步

3.2 评估指标

主要指标：均方误差（MSE）

单步MSE：评估单步预测的准确性
推演MSE：评估长期预测的准确性

辅助指标：分布度量

最优传输（Optimal Transport）：使用Wasserstein距离
最大均值差异（MMD）：使用高斯核

这些指标对粒子排列不敏感，更适合评估材料的整体分布。

四、实验结果

4.1 模拟多种复杂材料

GNS在所有测试的材料上都表现出色：

从Table 1的数据可以看出：

数据集	粒子数	时间步	单步MSE (×10⁻⁹)	推演MSE (×10⁻³)
WATER-3D	13k	800	8.66	10.1
SAND-3D	20k	350	1.42	0.554
GOOP-3D	14k	300	1.32	0.618

关键发现：

模型可以扩展到19k粒子（远超之前的方法）
虽然只训练单步预测，但可以稳定推演数千个时间步
视觉效果上，模型生成的轨迹很难与真实仿真区分

4.2 多材料交互

令人印象深刻的是，单一模型可以同时学习多种材料及其相互作用：

在MULTIMATERIAL数据集中：

水、沙、goop同时存在
需要学习材料间交互的"叉积空间"（水-水、沙-沙、水-沙等）
表现出丰富的行为：沙和goop形成临时半刚性障碍物，水在其周围流动

4.3 泛化能力

GNS展现了强大的泛化能力，远超训练分布：

4.3.1 粒子数量泛化

在WATERRAMPS数据集上训练（2.5k粒子）：

测试时添加持续的水流入口
最终场景包含28k粒子（训练时的10倍以上）
推演2500步（训练时的4倍）
仍能准确预测高度混沌的动力学

4.3.2 空间尺度泛化

更极端的测试：

训练域面积：约1.0 × 1.0
测试域面积：8.0 × 4.0（32倍大）
最终粒子数：85k（34倍多）
推演步数：5000（8倍长）

4.3.3 未见形状泛化

在MULTIMATERIAL上训练后，应用于包含：

河马形状的goop块
各种未见过的形状
从半空下落

模型成功泛化到这些全新的场景。

4.4 关键架构选择分析

论文进行了全面的消融实验，识别出5个关键因素：

1. 消息传递步数（M）

影响最大的因素：

M=0（无消息传递）：性能最差
M增加，性能显著提升
M=10时性能优异（论文默认选择）
M=15时略有改善，但计算成本增加

从Figure 4(a,b)可以看出，推演误差从M=3的约3×10⁻²降到M=10的约1×10⁻³。

原因：更多步数允许信息传播更远，计算更复杂的交互。

2. 共享vs非共享参数

非共享参数明显更好：

共享参数：类似循环模型，参数量少
非共享参数：类似深度网络，参数量为M倍

从Figure 4(c,d)看，非共享参数的推演MSE约为共享参数的1/2。

3. 连接半径（R）

更大的R带来更好的性能：

R从0.003到0.03，性能持续改善
更大的R增加边数，计算成本增加

Figure 4(e,f)显示R=0.015（默认值）时性能与更大的R相近。

4. 训练噪声尺度

存在最优噪声水平：

无噪声：推演误差高
噪声过大：单步误差和推演误差都高
噪声尺度= 0.0003（默认）：推演误差最低

Figure 4(g,h)清晰展示了这个U型曲线关系。

5. 相对vs绝对编码

相对编码明显优于绝对编码：

绝对编码：使用绝对位置信息
相对编码：使用相对位移

从Figure 4(i,j)看，相对编码的推演MSE约为绝对编码的1/3。

原因：物理过程本质上是空间平移不变的，相对编码的归纳偏置与此一致。

4.5 与现有方法的对比

4.5.1 vs. DPI (Li et al., 2018)

在BOXBATH数据集上：

DPI需要专门的层次化机制来处理刚体
DPI强制刚体粒子间保持相对位移
GNS无需任何特殊处理，仅将材料类型作为输入特征

结果：GNS完美保持了盒子的形状，同时准确模拟了流体动力学。

4.5.2 vs. CConv (Ummenhofer et al., 2020)

论文实现了CConv并在6个数据集上进行了对比：

从图中可以看出：

GNS在所有6个数据集上都优于CConv
在BOXBATH上，CConv的盒子失去形状（Figure 4(l)）
在复杂材料（如goop）上，CConv表现挣扎

定量结果示例：

数据集	GNS推演MSE	CConv推演MSE
BoxBath	4.2×10⁻³	~8×10⁻³
Water-3D-S	9.52×10⁻³	~12×10⁻³
Goop	1.89×10⁻³	~4×10⁻³

原因：

CConv专门针对类水流体设计
GNS是更通用的模型，容量更大
GNS使用多步消息传递和更灵活的函数近似器

4.6 计算效率

论文还报告了推理时间（补充材料C.6）：

以GOOP-3D为例：

真实模拟器（MPM，CPU）：0.199秒/步
GNS（V100 GPU，含邻域计算）：0.247秒/步（124%）
GNS（仅模型推理）：0.109秒/步（55%）

结论：GNS的推理速度与传统模拟器相当，且大部分时间花在邻域图构建上，而非神经网络推理。

结语

GNS框架展示了深度学习在科学计算领域的巨大潜力。通过巧妙地结合图神经网络、粒子表示和精心设计的训练策略，它实现了通用、准确、可扩展的物理仿真。这不仅是机器学习的胜利，也是对物理仿真范式的重新思考。

随着计算能力的提升和算法的进一步改进，我们有理由期待，学习型仿真器将在未来的科学研究和工程实践中发挥越来越重要的作用。