零
明天<线性代数>期末考,争取满绩
汇总了线性代数的所有知识点
不写题+我的理解(不太习惯用专业术语)
(目的是深入理解<线性代数> 期末拿个好分数)
内容多,先看目录哈
祝我明天好运
determinant(行列式)
本质就是一个数
必须是n*n的矩阵,才有行列式
行列式就是一个矩阵在一个运算规则后的结果
行列式就是一个数,运算符合一个数的运算规则
inversion number(逆序数N)
概念 : 对于一个n级排列(1,2,3,4,...n(数字顺序不固定,但是要包含完整) ),逆序数就是统计"前面数>后面数"的数对个数N
对于逆序数N,我们只关心它是奇数还是偶数(不关心它是多少)
先说一个结论 : 一个N级排列,交换相邻的两个数一次,N的奇偶性一定改变
(自己想想就可以推导,
对于其他数对,把这两个相邻的数看成一个整体,其他数据之间的大小关系是不变的,
对于这两个数对,一定是奇偶性变了,N+1或者-1)
再推广一下 : 既然相邻的两个数交换,奇偶性改变一次,那么交换任意两个数都可以看作是---不断的交换相邻的数(类似于计算机中交换数组中的两个数据元素),我们发现交换的次数一定是奇数,所以得到结论 : 交换任意两个数,这组数据的逆序数的奇偶性一定改变
eg :
N(123)=0(偶数)
N(3412)=2+2+0+0=4(偶数)
N(14532)=0+2+2+1+0=5(奇数)
行列式定义
取出不同行不同列的数据,符号是(-1)N(行排列)+N(列排列)

按行定义 : 先确定行排列是(1234...row) ,(-1)N(行排列)=(-1)0=1,符号直接由列排列决定
按列定义 : 同样的方法
行列式按行展开
取出一行元素,a11,a12...a1n,
D = a11 * A11 + a12 * A12+...+a1n * A1n
每一个元素和对应的代数余子式乘积之和
按列展开也是一样道理
行列式性质
(对行成立的性质,对列也成立)
下面都以行为例
主对角型行列式计算
D = 对角元素相乘
副对角型行列式计算
D = (-1)N(n,n-1,n-2,n-3...2,1) *对角元素相乘 = (-1)n*(n-1)/2 * 对角元素相乘
(本质还是定义展开)
行列式转置,值不变
推导 :
回归行列式的定义,原行列式按照行展开 就是 转置后的行列式按照列展开
(完全一样的哈,很好理解)
行列式交换两行,值反号
本质就是因为,展开的时候,每一项的逆序数的奇偶性改变了,就可以提取一个-1
行列式有两行一样,行列式值为0
直接交换这两行,-D=D,所以D=0
行列式一行k,值k(倍乘性质)
本质就是因为,展开的时候,每一项都*k,就可以提取一个k
行列式可拆性质

把某一行的k倍 +到 另外一行上,值不变
相当于 + 0
matrix(矩阵)
就是一个数表/线性变换
矩阵相等
两个矩阵完全一样,才相等
矩阵加法
前提要是同型矩阵 (行数相同,列数也相同)
每一个位置都相加
数 * 矩阵
每一个元素都*这个数
矩阵 * 矩阵
这张图很详细了

注意 : 矩阵A矩阵B 是有前提的,结果的型是 A的行B的列
AB 和 BA不一样
方阵的性质

可逆矩阵 && 分块矩阵
初等变换求逆矩阵

分块矩阵
AB=BA=E


矩阵公式大总结

记忆方法不说了,理解了就不用背
system of equations(方程组) && rank(秩)
由方程组得到一个矩阵(A | b)
秩 && 解的情况
秩 = 有效方程的个数 = 行阶梯/行最简矩阵的非零行行数 = 主元个数 (这三者都是相通的)
秩就可以表示一个方程组有效方程的个数
首先要知道r(A) 一定是 <= r(A | b)的
如果 r(A) < r(A | b) 说明有非法的行 (0=非零数) 一定是无解
如果 r(A) = r(A | b) 并且r(A)=未知量的个数,一定是唯一解
如果 r(A) = r(A | b) 并且r(A)<未知量的个数,一定是无穷多解(eg : 只有2个方程,要解3个未知数,一定是无穷多解)
秩的本质
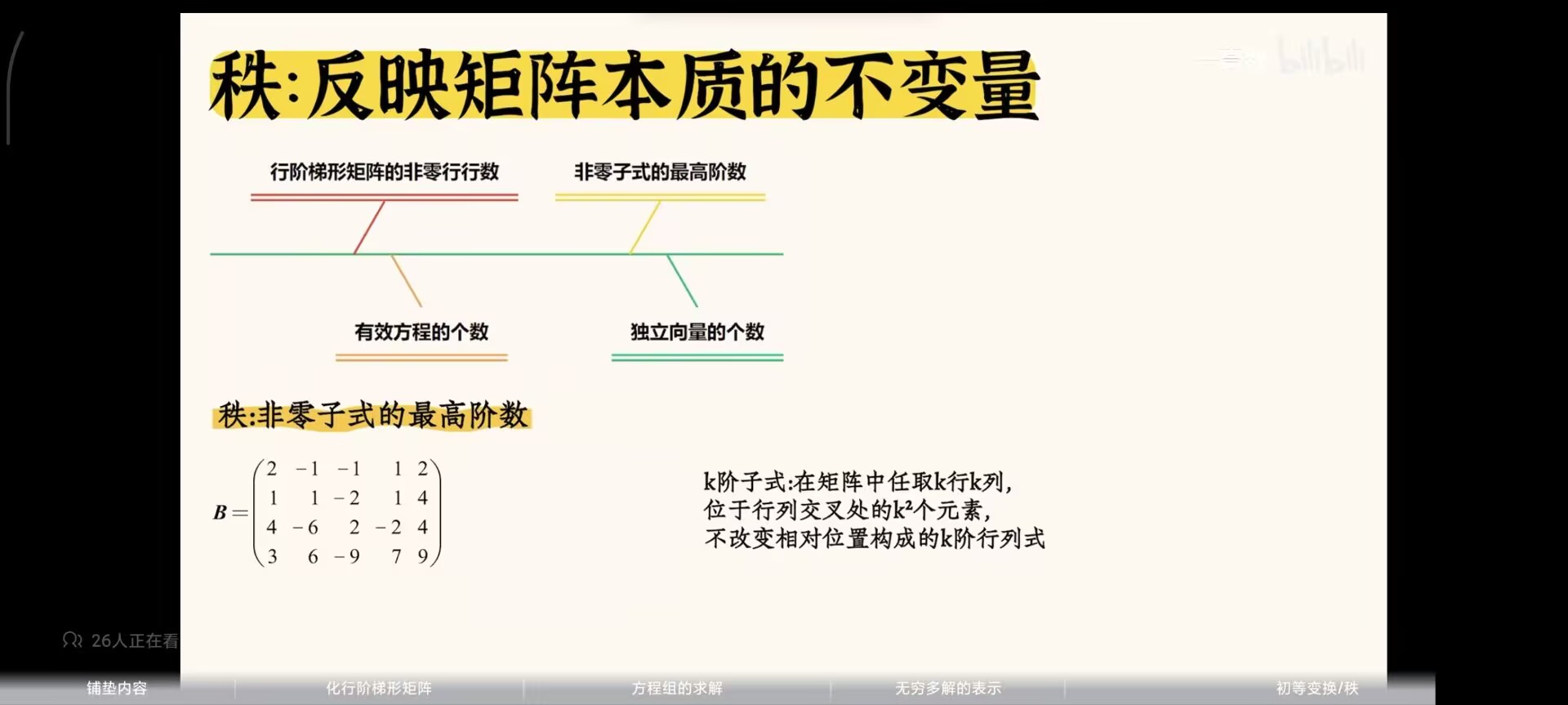
秩的不等式
越乘越小,越拼越大,分开加最大

行阶梯型矩阵 && 行最简型矩阵

vector(向量)
线性相关性+特征值和特征向量+相似对角化+相似(概念本质理解 没有计算公式 就是让你在几何空间中理解)
看我的这一集 : 线性代数(通透版02集)线性相关性+特征值和特征向量+相似对角化+相似(概念本质理解 没有计算公式 就是让你在几何空间中理解)
线性代数(通透版02集)线性相关性+特征值和特征向量+相似对角化+相似(概念本质理解 没有计算公式 就是让你在几何空间中理解)
这个是很详细的我的理解(人话版),在本篇文章就不在过多赘述了
正交相似对角化
施密特正交化

正交化后的矩阵Q满足 :
QTQ = Q QT
正交化+单位化 后的矩阵满足 :
QTQ = Q QT = E
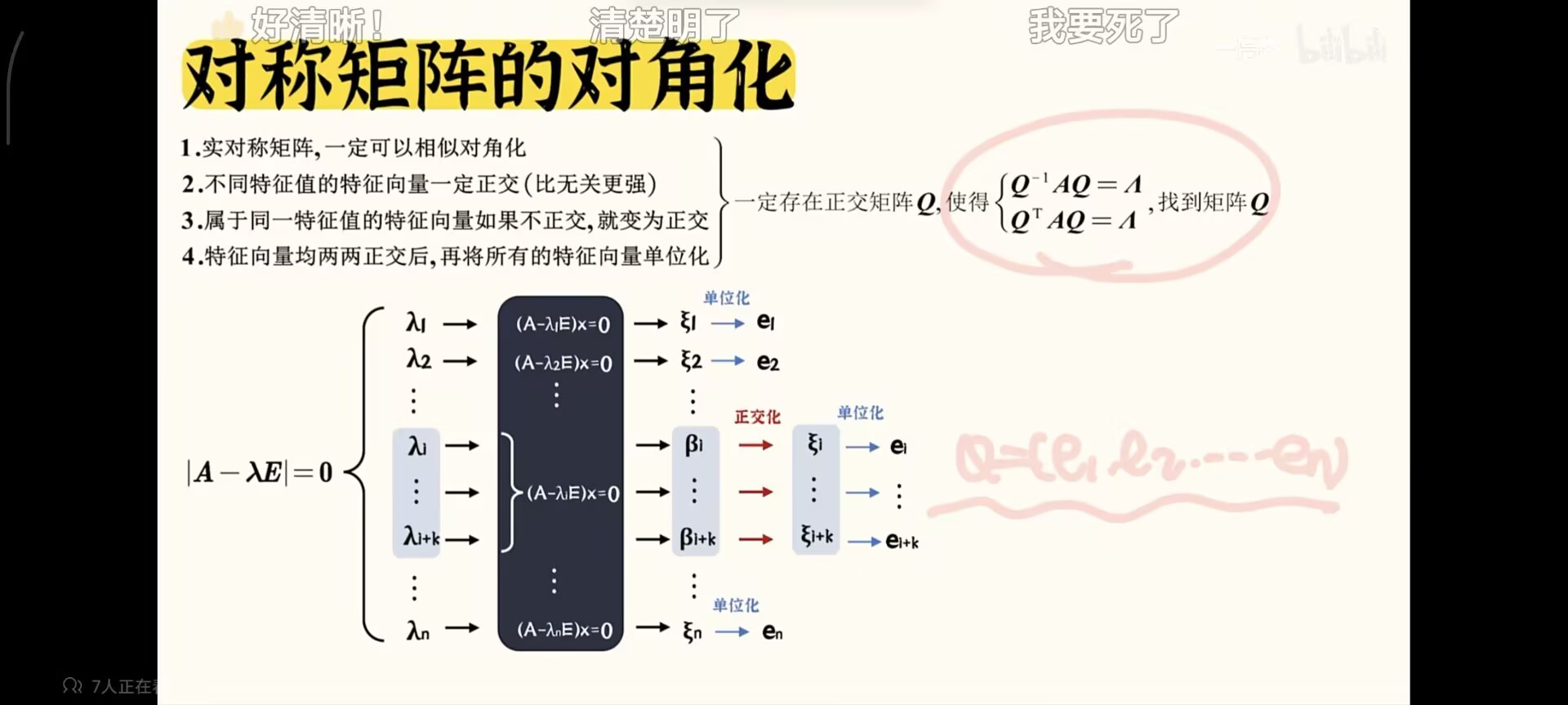
对称矩阵的对角化
实对称矩阵一定可以相似对角化
P-1A P = 对角阵
把P的列向量进行正交化+单位化 得到矩阵Q
QTA Q = Q-1A Q= 对角阵
(其中这个Q,满足QTQ = Q QT = E)
两个矩阵相似-->得出 : 这两个矩阵的数值(tr , determinant , 特征值 ...)都一样
二次型
(其实二次型的题就是总和运用所有前面的知识了哈)
首先要知道 :
对称矩阵一定可以相似对角化
实对称矩阵一定可以正交相似对角化
(为什么是这样,我以后再证明,没时间了,明天就考试了)
二次型基础

特征值 && 特征向量 的本质
在之前专栏讲过了
二次型的标准型&&规范性
标准型的系数就是特征值

线性变换的本质
之前的专栏讲过了

正定二次型

简单来说 : 对于正定二次型,只要x!=0,y都>0
正定二次型的顺序主子式都>0
这个关于二次型主要还是做题,都是和前面内容重合了,不再说了
最后,感谢一数
(写到后面发现自己写的没有一数好,直接用一数的了哈,重在理解)