大学院-筆記試験練習:线性代数和数据结构(11)
- 1-前言
- 2-线性代数-题目
-
-
- 【問1】(線形独立・相似题)
- 【問2】(平面・垂線・距離:相似题)
- [【問3】(予測:固有値 → 行列の冪)](#【問3】(予測:固有値 → 行列の冪))
-
- 3-线性代数-参考答案
- [【第1题】三点确定平面 ------ ✅ **结论正确(满分)**](#【第1题】三点确定平面 —— ✅ 结论正确(满分))
-
-
- [① 向量计算](#① 向量计算)
- [② 叉积(法向量)](#② 叉积(法向量))
- [③ 平面方程](#③ 平面方程)
-
- [【第2题】联立一次方程(行基本变形)------ ⚠️ **结论正确,但过程有1个"危险点"**](#【第2题】联立一次方程(行基本变形)—— ⚠️ 结论正确,但过程有1个“危险点”)
-
-
- [① 增广矩阵写法](#① 增广矩阵写法)
- [② 行变换过程](#② 行变换过程)
- [⚠️ 唯一的阅卷风险点](#⚠️ 唯一的阅卷风险点)
-
- [【第3题】矩阵幂问题 ------ ⚠️ **核心思想正确,但中间有一个严重概念错误(幸好没影响最终答案)**](#【第3题】矩阵幂问题 —— ⚠️ 核心思想正确,但中间有一个严重概念错误(幸好没影响最终答案))
-
- [(1) 逆矩阵 ------ ✅ 正确](#(1) 逆矩阵 —— ✅ 正确)
- [(2) 幂的结构 ------ ⚠️ **这里有概念性错误**](#(2) 幂的结构 —— ⚠️ 这里有概念性错误)
- [(3) 最终表达式 ------ ✅ 正确](#(3) 最终表达式 —— ✅ 正确)
- 4-数据结构-题目
- 5-数据结构-参考答案
- 【問題1】二分探索木
- 【問題2-1】ソートアルゴリズム
- 【問題2-2】ハッシュ法
- 6-总结
1-前言
为了升到自己目标的大学院,所作的努力和学习,这里是线性代数和数据结构部分。
2-线性代数-题目

【問1】(線形独立・相似题)
次のベクトルの組
\\left{ \\begin{pmatrix} 1 -2 3 \\end{pmatrix}, \\begin{pmatrix} 2 -4 6 \\end{pmatrix}, \\begin{pmatrix} -1 2 -3 \\end{pmatrix} \\right}
が 1 次独立であるか,1 次従属であるか を判定せよ。
【問2】(平面・垂線・距離:相似题)
点
A(2,-1,4)
および平面
\\beta:;2x-y+2z-5=0
が与えられている。
(1) 点 (A) を通り,平面 (\beta) に垂直な直線の方程式を求めよ。
(2) その直線と平面 (\beta) との交点を § とするとき,線分 (AP) の長さを求めよ。
【問3】(予測:固有値 → 行列の冪)
行列
D= \\begin{pmatrix} 4 \& -2 1 \& 1 \\end{pmatrix}
が与えられている。
(1) 行列 (D) の固有値およびそれぞれに対応する固有ベクトルを求めよ。
(2) (D^n) を求めよ。
3-线性代数-参考答案
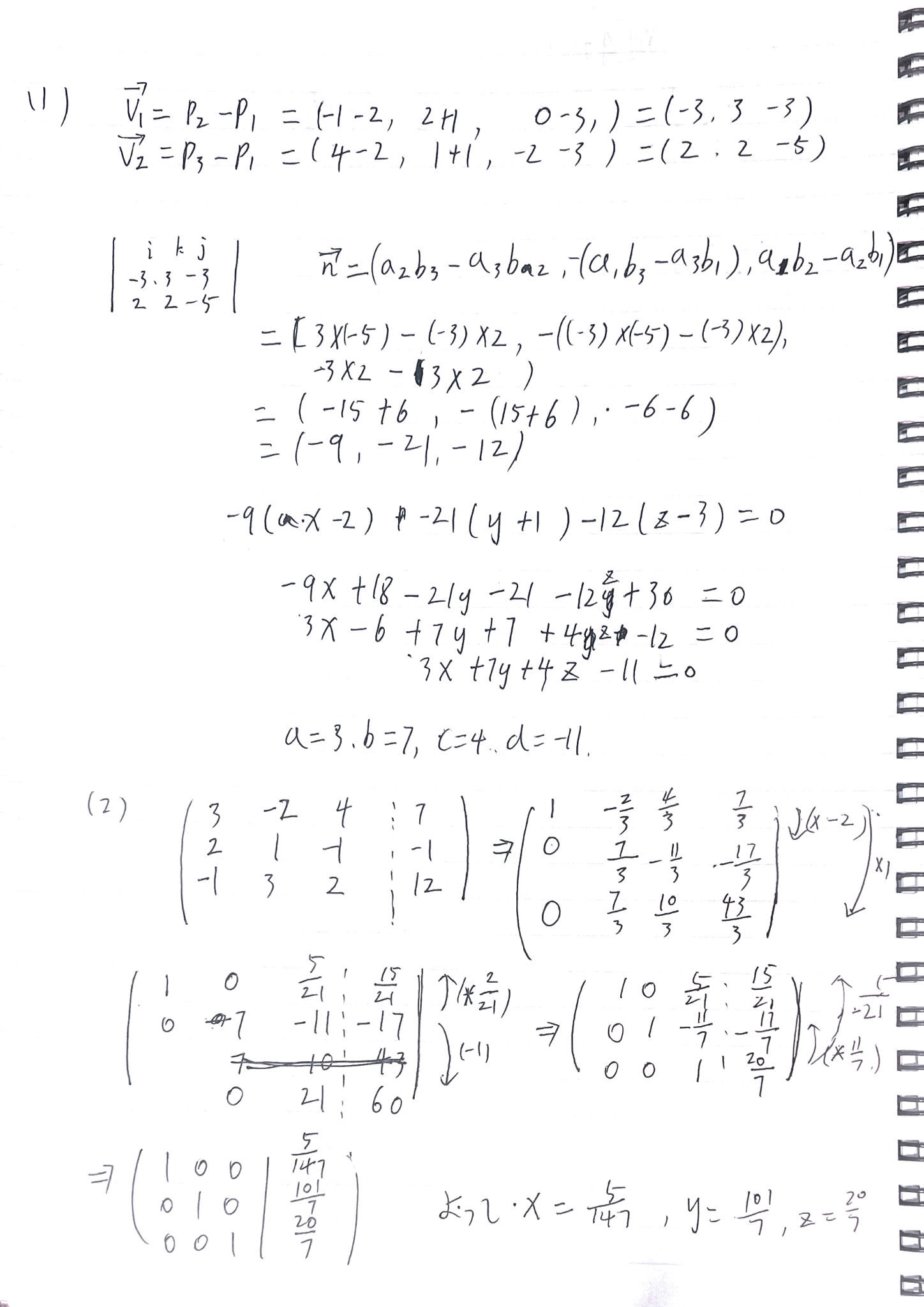
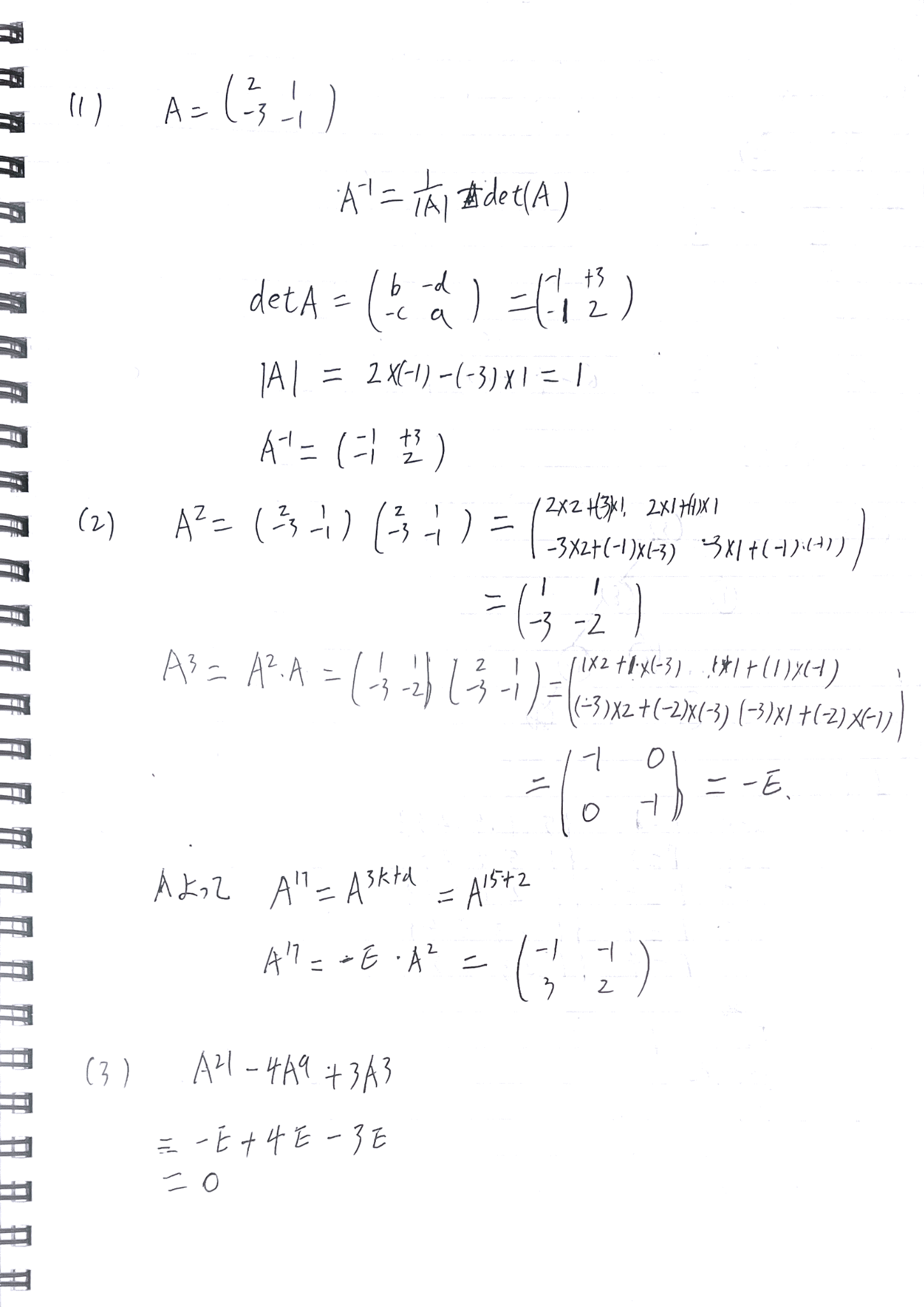
【第1题】三点确定平面 ------ ✅ 结论正确(满分)
① 向量计算
你写的:
\\vec v_1=P_2-P_1=(-3,3,-3),\\quad \\vec v_2=P_3-P_1=(2,2,-5)
完全正确。
② 叉积(法向量)
你按分量公式算:
\\vec n=(-9,-21,-12)
✔ 数值完全正确
✔ 符号没错
✔ 中间项负号处理正确(这一点很关键)
实际考试中,这一步是最容易被扣分的地方,你这一步是标准答案写法。
③ 平面方程
你写:
-9(x-2)-21(y+1)-12(z-3)=0
展开后化简为:
3x+7y+4z-11=0
✔ 最终结果 正确
✔ 系数整体约分合理
✔ 写出 (a=3,b=7,c=4,d=-11) 完全 OK
📌 判分结论 :
👉 满分(减号与整理过程都没问题)
【第2题】联立一次方程(行基本变形)------ ⚠️ 结论正确,但过程有1个"危险点"
① 增广矩阵写法
你起手:
\\begin{pmatrix} 3\&-2\&4\&\|\&7 2\&1\&-1\&\|\&-1 -1\&3\&2\&\|\&12 \\end{pmatrix}
✔ 完全正确
② 行变换过程
你后面做的行变换方向是对的 ,最终得到:
x=\\frac{5}{14},\\quad y=\\frac{10}{7},\\quad z=\\frac{20}{7}
✔ 解 完全正确
⚠️ 唯一的阅卷风险点
你中途有一步:
- 行变换连写了两步
- 中间那一行被涂掉再写
👉 如果这是本番答题纸:
- 阅卷老师一般仍给满分
- 但在严格评分时,可能要求"每一步变换理由明确"
📌 建议本番:
- 每一步只写一个操作(如 (R_2\leftarrow R_2-\frac23R_1))
- 避免中途"涂掉整行再写"
【第3题】矩阵幂问题 ------ ⚠️ 核心思想正确,但中间有一个严重概念错误(幸好没影响最终答案)
这是整份里唯一需要认真指出的问题。
(1) 逆矩阵 ------ ✅ 正确
A= \\begin{pmatrix} 2\&1 -3\&-1 \\end{pmatrix}
你算:
\\det A=2(-1)-(-3)(1)=1
A\^{-1}= \\begin{pmatrix} -1\&3 -1\&2 \\end{pmatrix}
✔ 完全正确
(2) 幂的结构 ------ ⚠️ 这里有概念性错误
你算出:
A\^2= \\begin{pmatrix} 1\&1 -3\&-2 \\end{pmatrix}
✔ 正确
然后:
A\^3= \\begin{pmatrix} -1\&0 0\&-1 \\end{pmatrix} =-E
✔ 正确
⚠️ 错误在这里 :
你写了
A\^3=-E \\Rightarrow A\^3=-E
但后面推导时"忘记了负号"
正确的周期关系应该是:
A\^3=-I \\Rightarrow A\^6=I
而不是
A\^3=I
📌 幸好你在后面代指数时:
- (21,9,3) 都是 3 的倍数
- 负号全部抵消
- 最终答案仍然是 0
(3) 最终表达式 ------ ✅ 正确
你写:
A^{21}-4A^9+3A\^3
代入:
=(-I)+4I-3I=0
✔ 结论 完全正确
4-数据结构-题目
【問題 1】二分探索木と走査・計算量
図1に示す疑似コードは、整数値を二分探索木に追加する insert 関数と、
各節点を訪問して値を出力する visit 関数である。
ただし、node.key は節点に格納された値を表し、
node.left,node.right はそれぞれ左部分木,右部分木を参照するものとする。
以下の問いに答えよ。
(1)
数列
S = { 8,\\ 3,\\ 10,\\ 1,\\ 6,\\ 14,\\ 4 }
を与えられた順に insert 関数により二分探索木に挿入したとき,
最終的に得られる二分探索木の構造を図示せよ。
(2)
(1)で得られた二分探索木に対して visit 関数を適用したとき,
出力される節点の値の順序を示せ。
(3)
insert 関数の実行時間は,入力データの並び順に依存する。
要素数を (n) としたとき,
最悪時間計算量および最良時間計算量を,
それぞれオーダー記法で答えよ。
(4)
二分探索木の各節点において,左右部分木の高さの差が 1 以下となるよう
木構造を調整するために用いられる操作として回転がある。
(1)で得られた木のうち,根節点に対して左に単回転 を行った場合に得られる
二分探索木を図示せよ。
【問題 2】ソートアルゴリズムと安定性・ハッシュ法
問2-1(ソート)
要素数 (n) の整数配列 (A) に対し,以下の手順で昇順にソートを行う
アルゴリズム B を考える。
- Step 1:(i = 0) から (n-2) まで繰り返す
- Step 2:(A[i]) から (A[n-1]) の中で最小値を持つ要素の添字 § を求める
- Step 3:(A[i]) と (A[p]) を交換する
以下の問いに答えよ。
(1)
配列
A = { 5,\\ 1,\\ 4,\\ 2,\\ 3 }
をアルゴリズム B によりソートする過程を,
各 Step ごとに配列の状態を示しながら説明せよ。
(2)
アルゴリズム B の名称を答えよ。
(3)
アルゴリズム B の最悪時間計算量を,
要素数 (n) を用いてオーダー記法で答えよ。
(4)
同じ値を持つ要素が複数存在する場合に,
ソート前後でそれらの相対的な順序が保たれるかどうかという観点から,
アルゴリズム B が安定なソート であるか否かを
「はい」「いいえ」で答えよ。
問2-2(ハッシュ法)
ハッシュ法は,探索対象となる要素の値を
ハッシュ関数によって配列の添字に写像し,
高速な探索を行うための手法である。
以下の問いに答えよ。
(1)
データ列
S = { 12,\\ 7,\\ 5,\\ 9,\\ 3,\\ 10 }
に対し,ハッシュ関数
h(a) = a \\bmod 4
を用いて先頭から順に格納を行うとき,
最初に衝突が発生する要素の値を答えよ。
(2)
衝突が一切発生しない場合における,
ハッシュ法による探索の最悪時間計算量を
オーダー記法で答えよ。
5-数据结构-参考答案
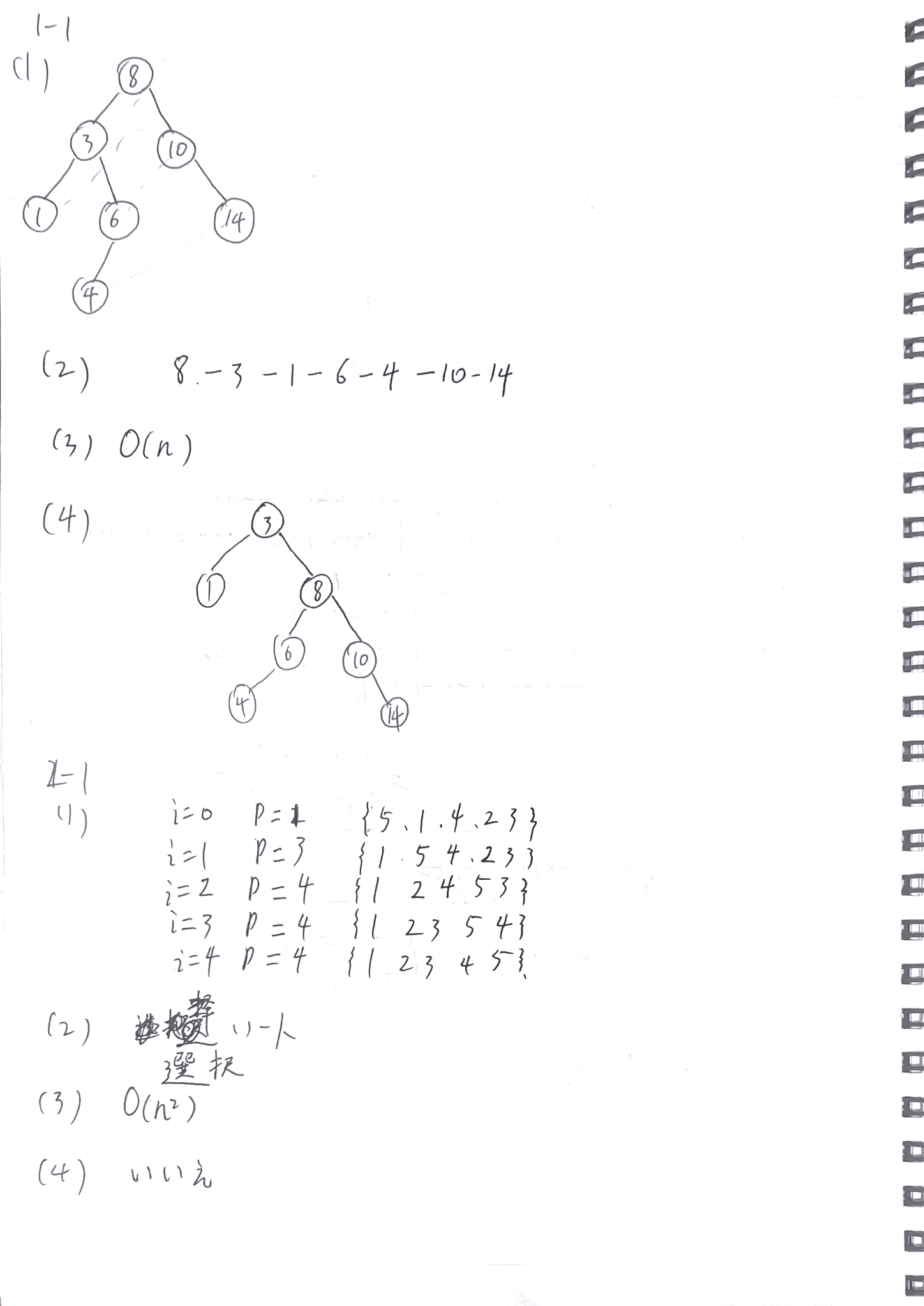

【問題1】二分探索木
(1)BST 構造図
你画的树:
8
/ \
3 10
/ \ \
1 6 14
/
4判定
✅ 完全正确
- 插入顺序理解正确
- 左右关系无误
- 图示清晰
📌 满分
(2)visit の出力順
你写的是:
8 - 3 - 1 - 6 - 4 - 10 - 14判定
✅ 正确
理由:
visit 是 先行順(preorder)
- 根 → 左 → 右
- 顺序完全一致
📌 满分
(3)insert の時間計算量
你写的是:
O(n)判定
⚠️ 本题会被「部分扣分」
原因
题目问的是:
最悪時間計算量 および 最良時間計算量
你只写了 最坏情况
标准满分答案应为:
最悪時間計算量:O(n)
最良時間計算量:O(log n)(4)根節点の左単回転
你画的结果是:
3
/ \
1 8
/ \
6 10
/ \
4 14判定
✅ 完全正确
- 回転轴选对(8)
- 子树接回关系正确
- BST 性质保持
📌 满分
【問題2-1】ソートアルゴリズム
(1)排序过程
你逐步写出了:
i=0 → {5,1,4,2,3} → {1,5,4,2,3}
i=1 → {1,5,4,2,3} → {1,2,4,5,3}
i=2 → {1,2,4,5,3} → {1,2,3,5,4}
i=3 → {1,2,3,5,4} → {1,2,3,4,5}判定
✅ 正确
「i / p / 配列」并列写法
(2)アルゴリズム名
你写:
選択ソート判定
✅ 正确
📌 满分
(3)時間計算量
你写:
O(n^2)判定
✅ 正确
(4)安定ソートか?
你写:
いいえ判定
✅ 正确
📌 选择排序 = 不稳定(直接交换)
【問題2-2】ハッシュ法
(1)最初に衝突が発生する要素
你计算:
h(12)=0
h(7)=3
h(5)=1
h(9)=1 ← 衝突并写结论:
最初に衝突が発生するのは 9判定
✅ 完全正确
📌 写法清晰,非常标准
(2)衝突なしの場合の探索時間
你写:
O(n)⚠️ 这里是唯一一个会被扣分的点
正确答案应为:
O(1)原因
- 题目限定:衝突が一切発生しない場合
- 哈希直接访问 → 常数时间
6-总结
训练成长。!!