2026-01-05期末复习-计算机图形学计算题

计算题试题

分辨率 1024×7681024\times 7681024×768，总像素数先算清楚：

1024×768=786,4321024\times 768 = 786{,}4321024×768=786,432 个像素。

可显示色彩 102410241024 色 ⇒ 每个像素需要的位数是
log⁡2(1024)=10\log_2(1024)=10log2(1024)=10 bit/像素（因为 1024=2101024=2^{10}1024=210）。

所以帧缓冲大小：

• 总比特数 ：786,432×10=7,864,320786{,}432 \times 10 = 7{,}864{,}320786,432×10=7,864,320 bit
• 换算成字节 ：7,864,320/8=983,0407{,}864{,}320 / 8 = 983{,}0407,864,320/8=983,040 Byte
• 换算成 KiB / MiB ：
  983,040/1024=960983{,}040 / 1024 = 960983,040/1024=960 KiB
  960/1024=0.9375960 / 1024 = 0.9375960/1024=0.9375 MiB

答案：帧缓冲至少需要 983,040 B = 960 KiB ≈ 0.94 MiB。

（现实硬件里通常会按 16 bit/像素对齐存储，那就会更大，但题目按理论最小值就是上面这个。）

该问题可视为绕点 (2,6)(2,6)(2,6) 的非均匀缩放变换。该变换可通过平移与缩放的复合实现，即先将该点平移至原点，执行缩放变换，再将坐标系平移回原位置。

相应的齐次坐标变换矩阵可表示为

M=T(2,6) S T(−2,−6), M = T(2,6)\, S \, T(-2,-6), M=T(2,6)ST(−2,−6),

其中

T(−2,−6)=10−201−6001,S=20000.20001,T(2,6)=102016001. T(-2,-6)= \begin{bmatrix} 1&0&-2\\ 0&1&-6\\ 0&0&1 \end{bmatrix},\quad S= \begin{bmatrix} 2&0&0\\ 0&0.2&0\\ 0&0&1 \end{bmatrix},\quad T(2,6)= \begin{bmatrix} 1&0&2\\ 0&1&6\\ 0&0&1 \end{bmatrix}. T(−2,−6)= 100010−2−61 ,S= 20000.20001 ,T(2,6)= 100010261 .

为快速得到等效单矩阵，可利用二维仿射变换在齐次坐标下的分块形式

Mi=Aiti01, M_i= \begin{bmatrix} A_i & \mathbf t_i\\ 0 & 1 \end{bmatrix}, Mi=Ai0ti1,

其中 Ai∈R2×2A_i\in\mathbb R^{2\times2}Ai∈R2×2 为线性部分，ti∈R2\mathbf t_i\in\mathbb R^{2}ti∈R2 为平移部分。由分块矩阵乘法可得复合规则

A3t301A2t201A1t101=A3t301A2A1A2t1+t201=A3A2A1A3A2t1+A3t2+t301. \begin{aligned} \begin{bmatrix} A_3 & \mathbf t_3\\ 0 & 1 \end{bmatrix} \begin{bmatrix} A_2 & \mathbf t_2\\ 0 & 1 \end{bmatrix} \begin{bmatrix} A_1 & \mathbf t_1\\ 0 & 1 \end{bmatrix} &= \begin{bmatrix} A_3 & \mathbf t_3\\ 0 & 1 \end{bmatrix} \begin{bmatrix} A_2A_1 & A_2\mathbf t_1+\mathbf t_2\\ 0 & 1 \end{bmatrix} \\ &= \begin{bmatrix} A_3A_2A_1 & A_3A_2\mathbf t_1 + A_3\mathbf t_2 + \mathbf t_3\\ 0 & 1 \end{bmatrix}. \end{aligned} A30t31A20t21A10t11=A30t31A2A10A2t1+t21=A3A2A10A3A2t1+A3t2+t31.

将 T(2,6)T(2,6)T(2,6)、SSS、T(−2,−6)T(-2,-6)T(−2,−6) 分别写成分块形式，有

T(2,6): A1=I, t1=26,S: A2=2000.2, t2=0,T(−2,−6): A3=I, t3=−2−6. T(2,6):\ A_1=I,\ \mathbf t_1=\begin{bmatrix}2\\6\end{bmatrix},\qquad S:\ A_2=\begin{bmatrix}2&0\\0&0.2\end{bmatrix},\ \mathbf t_2=\mathbf 0,\qquad T(-2,-6):\ A_3=I,\ \mathbf t_3=\begin{bmatrix}-2\\-6\end{bmatrix}. T(2,6): A1=I, t1=26,S: A2=2000.2, t2=0,T(−2,−6): A3=I, t3=−2−6.

因此总体线性部分为

A=A1A2A3=I⋅2000.2⋅I=2000.2, A=A_1A_2A_3 = I\cdot \begin{bmatrix}2&0\\0&0.2\end{bmatrix}\cdot I = \begin{bmatrix}2&0\\0&0.2\end{bmatrix}, A=A1A2A3=I⋅2000.2⋅I=2000.2,

总体平移部分为

t=A1A2t3+A1t2+t1=2000.2−2−6+26=−4−1.2+26=−24.8. \mathbf t = A_1A_2\mathbf t_3 + A_1\mathbf t_2 + \mathbf t_1 = \begin{bmatrix}2&0\\0&0.2\end{bmatrix} \begin{bmatrix}-2\\-6\end{bmatrix} +\begin{bmatrix}2\\6\end{bmatrix} = \begin{bmatrix}-4\\-1.2\end{bmatrix} +\begin{bmatrix}2\\6\end{bmatrix} = \begin{bmatrix}-2\\4.8\end{bmatrix}. t=A1A2t3+A1t2+t1=2000.2−2−6+26=−4−1.2+26=−24.8.

从而得到等效单矩阵

M=At01=20−200.24.8001. M= \begin{bmatrix} A & \mathbf t\\ 0 & 1 \end{bmatrix} = \begin{bmatrix} 2&0&-2\\ 0&0.2&4.8\\ 0&0&1 \end{bmatrix}. M=A0t1= 20000.20−24.81 .

上述结果采用的是列向量表示下的左乘矩阵形式，即点坐标表示为列向量，几何变换通过矩阵左乘实现。在该表示下，复合变换的顺序与矩阵乘法顺序相反。若采用行向量表示，则变换矩阵需置于坐标向量右侧，相应的复合顺序与几何变换顺序一致，此时矩阵形式可由左乘矩阵取转置得到，两种表示方式在几何效果上是等价的。

---

先将旋转中心平移至原点，执行逆时针旋转 π/4\pi/4π/4，再将坐标系平移回原位置。

相应的齐次坐标变换矩阵可表示为

M=T(3,2) R(π/4) T(−3,−2), M = T(3,2)\, R(\pi/4)\, T(-3,-2), M=T(3,2)R(π/4)T(−3,−2),

其中

T(−3,−2)=10−301−2001,R(π/4)=cos⁡π4−sin⁡π40sin⁡π4cos⁡π40001,T(3,2)=103012001. T(-3,-2)= \begin{bmatrix} 1&0&-3\\ 0&1&-2\\ 0&0&1 \end{bmatrix},\quad R(\pi/4)= \begin{bmatrix} \cos\frac{\pi}{4}&-\sin\frac{\pi}{4}&0\\ \sin\frac{\pi}{4}&\cos\frac{\pi}{4}&0\\ 0&0&1 \end{bmatrix},\quad T(3,2)= \begin{bmatrix} 1&0&3\\ 0&1&2\\ 0&0&1 \end{bmatrix}. T(−3,−2)= 100010−3−21 ,R(π/4)= cos4πsin4π0−sin4πcos4π0001 ,T(3,2)= 100010321 .

代入 cos⁡π4=sin⁡π4=22\cos\frac{\pi}{4}=\sin\frac{\pi}{4}=\frac{\sqrt{2}}{2}cos4π=sin4π=22 ，并对上述矩阵进行乘法运算，可得最终的复合变换矩阵

M=22−223−2222222−522001. M= \begin{bmatrix} \frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} & 3-\frac{\sqrt{2}}{2}\\4pt \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} & 2-\frac{5\sqrt{2}}{2}\\4pt 0&0&1 \end{bmatrix}. M= 22 22 0−22 22 03−22 2−252 1 .

该矩阵实现了以点 (3,2)(3,2)(3,2) 为不动点的逆时针 π/4\pi/4π/4 旋转变换。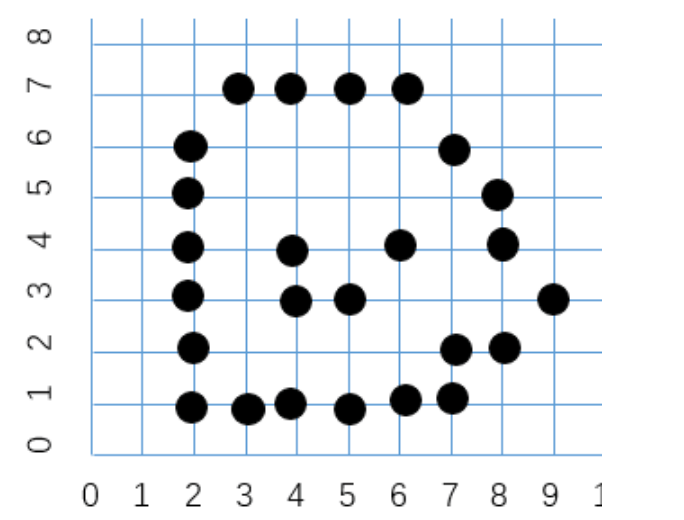

假设从种子设置为(5,4)

取种子点 s=(5,4)\mathbf{s}=(5,4)s=(5,4)。算法以栈 SSS 维护待处理像素：初始化 S=(5,4)S=(5,4)S=(5,4)；每轮从栈顶弹出像素 p\mathbf{p}p，将其着色，并按"右、上、左、下"依次检查四邻域像素 q\mathbf{q}q。若 q∉B\mathbf{q}\notin \mathcal{B}q∈/B 且尚未着色（并且未在栈内），则将 q\mathbf{q}q 入栈。栈空时算法终止。由此可得到从 (5,4)(5,4)(5,4) 出发、在四连通意义下与之连通且不跨越边界 B\mathcal{B}B 的所有内部像素被依次填充。

为记录"试填写堆栈的变化过程"，下面给出每次出栈并完成邻域检查后的栈内容（表示为"左底、右顶"）以及该步出栈像素：

• 初始：S=(5,4)S=(5,4)S=(5,4)

1. 出栈 (5,4)(5,4)(5,4)，入栈 (5,5)(5,5)(5,5)；S=(5,5)S=(5,5)S=(5,5)
2. 出栈 (5,5)(5,5)(5,5)，依序入栈 (6,5),(5,6),(4,5)(6,5),(5,6),(4,5)(6,5),(5,6),(4,5)；S=(6,5),(5,6),(4,5)S=(6,5),(5,6),(4,5)S=(6,5),(5,6),(4,5)
3. 出栈 (4,5)(4,5)(4,5)，入栈 (4,6),(3,5)(4,6),(3,5)(4,6),(3,5)；S=(6,5),(5,6),(4,6),(3,5)S=(6,5),(5,6),(4,6),(3,5)S=(6,5),(5,6),(4,6),(3,5)
4. 出栈 (3,5)(3,5)(3,5)，入栈 (3,6),(3,4)(3,6),(3,4)(3,6),(3,4)；S=(6,5),(5,6),(4,6),(3,6),(3,4)S=(6,5),(5,6),(4,6),(3,6),(3,4)S=(6,5),(5,6),(4,6),(3,6),(3,4)
5. 出栈 (3,4)(3,4)(3,4)，入栈 (3,3)(3,3)(3,3)；S=(6,5),(5,6),(4,6),(3,6),(3,3)S=(6,5),(5,6),(4,6),(3,6),(3,3)S=(6,5),(5,6),(4,6),(3,6),(3,3)
6. 出栈 (3,3)(3,3)(3,3)，入栈 (3,2)(3,2)(3,2)；S=(6,5),(5,6),(4,6),(3,6),(3,2)S=(6,5),(5,6),(4,6),(3,6),(3,2)S=(6,5),(5,6),(4,6),(3,6),(3,2)
7. 出栈 (3,2)(3,2)(3,2)，入栈 (4,2)(4,2)(4,2)；S=(6,5),(5,6),(4,6),(3,6),(4,2)S=(6,5),(5,6),(4,6),(3,6),(4,2)S=(6,5),(5,6),(4,6),(3,6),(4,2)
8. 出栈 (4,2)(4,2)(4,2)，入栈 (5,2)(5,2)(5,2)；S=(6,5),(5,6),(4,6),(3,6),(5,2)S=(6,5),(5,6),(4,6),(3,6),(5,2)S=(6,5),(5,6),(4,6),(3,6),(5,2)
9. 出栈 (5,2)(5,2)(5,2)，入栈 (6,2)(6,2)(6,2)；S=(6,5),(5,6),(4,6),(3,6),(6,2)S=(6,5),(5,6),(4,6),(3,6),(6,2)S=(6,5),(5,6),(4,6),(3,6),(6,2)
10. 出栈 (6,2)(6,2)(6,2)，入栈 (6,3)(6,3)(6,3)；S=(6,5),(5,6),(4,6),(3,6),(6,3)S=(6,5),(5,6),(4,6),(3,6),(6,3)S=(6,5),(5,6),(4,6),(3,6),(6,3)
11. 出栈 (6,3)(6,3)(6,3)，入栈 (7,3)(7,3)(7,3)；S=(6,5),(5,6),(4,6),(3,6),(7,3)S=(6,5),(5,6),(4,6),(3,6),(7,3)S=(6,5),(5,6),(4,6),(3,6),(7,3)
12. 出栈 (7,3)(7,3)(7,3)，依序入栈 (8,3),(7,4)(8,3),(7,4)(8,3),(7,4)；S=(6,5),(5,6),(4,6),(3,6),(8,3),(7,4)S=(6,5),(5,6),(4,6),(3,6),(8,3),(7,4)S=(6,5),(5,6),(4,6),(3,6),(8,3),(7,4)
13. 出栈 (7,4)(7,4)(7,4)，入栈 (7,5)(7,5)(7,5)；S=(6,5),(5,6),(4,6),(3,6),(8,3),(7,5)S=(6,5),(5,6),(4,6),(3,6),(8,3),(7,5)S=(6,5),(5,6),(4,6),(3,6),(8,3),(7,5)
14. 出栈 (7,5)(7,5)(7,5)，无新入栈；S=(6,5),(5,6),(4,6),(3,6),(8,3)S=(6,5),(5,6),(4,6),(3,6),(8,3)S=(6,5),(5,6),(4,6),(3,6),(8,3)
15. 出栈 (8,3)(8,3)(8,3)，无新入栈；S=(6,5),(5,6),(4,6),(3,6)S=(6,5),(5,6),(4,6),(3,6)S=(6,5),(5,6),(4,6),(3,6)
16. 出栈 (3,6)(3,6)(3,6)，无新入栈；S=(6,5),(5,6),(4,6)S=(6,5),(5,6),(4,6)S=(6,5),(5,6),(4,6)
17. 出栈 (4,6)(4,6)(4,6)，无新入栈；S=(6,5),(5,6)S=(6,5),(5,6)S=(6,5),(5,6)
18. 出栈 (5,6)(5,6)(5,6)，入栈 (6,6)(6,6)(6,6)；S=(6,5),(6,6)S=(6,5),(6,6)S=(6,5),(6,6)
19. 出栈 (6,6)(6,6)(6,6)，无新入栈；S=(6,5)S=(6,5)S=(6,5)
20. 出栈 (6,5)(6,5)(6,5)，无新入栈；S=\[\]S=\[\]S=\[\]（终止）

由上述过程可见，填充在有限步内终止（栈为空），并覆盖了所有与种子点 (5,4)(5,4)(5,4) 四连通可达且不穿越边界 B\mathcal{B}B 的内部像素。若实现中允许重复入栈（仅在出栈时判"是否已填充"），则最终填充区域不变，但堆栈序列会出现冗余项，记录表也会更长,可以采用扫描线种子填充算法解决这个问题

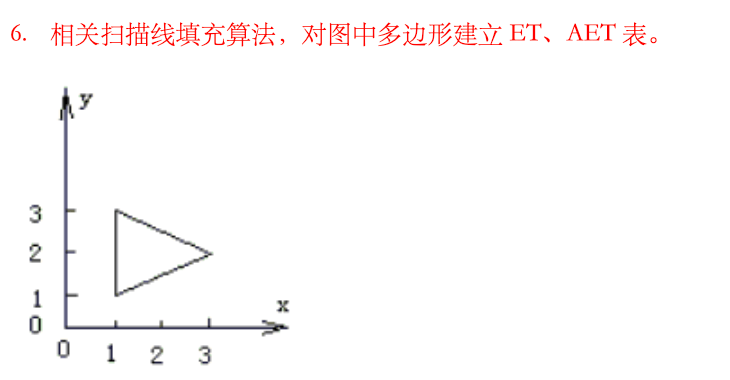
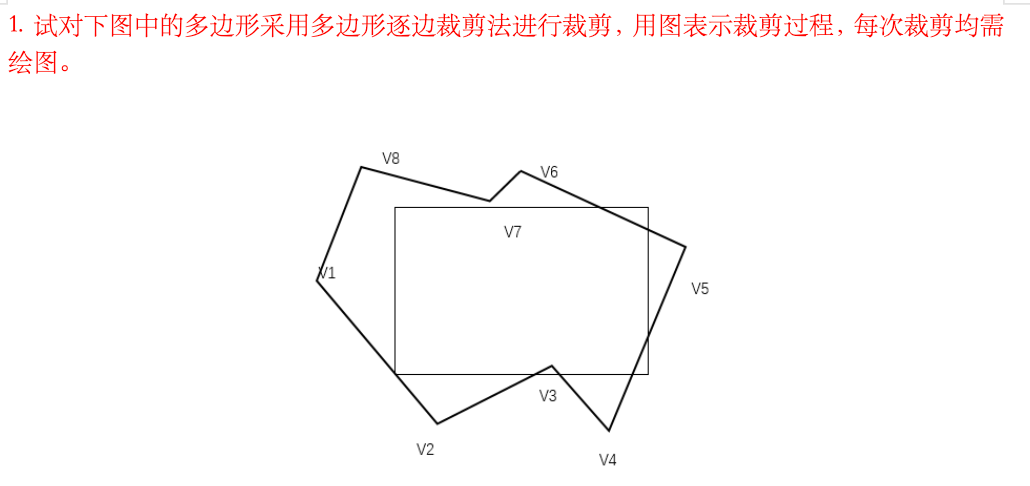
该多边形为三角形，其顶点可由图读出为

V1(1,1),V2(1,3),V3(3,2). V_1(1,1),\quad V_2(1,3),\quad V_3(3,2). V1(1,1),V2(1,3),V3(3,2).

采用扫描线填充的 ET/AET 构造约定：忽略水平边；每条边在 ET 中以 (ymax⁡,xymin⁡,Δx/Δy)(y_{\max},x_{y_{\min}},\Delta x/\Delta y)(ymax,xymin,Δx/Δy) 记录，并按 ymin⁡y_{\min}ymin 归入对应桶；AET 在每条扫描线 yyy 处先删除满足 y=ymax⁡y=y_{\max}y=ymax 的边，再插入 ETy，并按当前交点 xxx 升序维护；处理完该扫描线后令 x←x+Δx/Δyx\leftarrow x+\Delta x/\Delta yx←x+Δx/Δy 以用于下一条扫描线。

三条边分别为：

• e12:(1,1)→(1,3)e_{12}: (1,1)\to(1,3)e12:(1,1)→(1,3)，ymin⁡=1,ymax⁡=3y_{\min}=1,y_{\max}=3ymin=1,ymax=3，xymin⁡=1x_{y_{\min}}=1xymin=1，Δx/Δy=0\Delta x/\Delta y=0Δx/Δy=0；
• e23:(3,2)→(1,3)e_{23}: (3,2)\to(1,3)e23:(3,2)→(1,3)，ymin⁡=2,ymax⁡=3y_{\min}=2,y_{\max}=3ymin=2,ymax=3，xymin⁡=3x_{y_{\min}}=3xymin=3，Δx/Δy=−2\Delta x/\Delta y=-2Δx/Δy=−2；
• e31:(1,1)→(3,2)e_{31}: (1,1)\to(3,2)e31:(1,1)→(3,2)，ymin⁡=1,ymax⁡=2y_{\min}=1,y_{\max}=2ymin=1,ymax=2，xymin⁡=1x_{y_{\min}}=1xymin=1，Δx/Δy=2\Delta x/\Delta y=2Δx/Δy=2。

因此边表 ET（按桶 y=ymin⁡y=y_{\min}y=ymin）为：

• ET1: {(ymax⁡=3, x=1, Δx/Δy=0), (ymax⁡=2, x=1, Δx/Δy=2)}\mathrm{ET}1:\ \{(y_{\max}=3,\ x=1,\ \Delta x/\Delta y=0),\ (y_{\max}=2,\ x=1,\ \Delta x/\Delta y=2)\}ET1: {(ymax=3, x=1, Δx/Δy=0), (ymax=2, x=1, Δx/Δy=2)}
• ET2: {(ymax⁡=3, x=3, Δx/Δy=−2)}\mathrm{ET}2:\ \{(y_{\max}=3,\ x=3,\ \Delta x/\Delta y=-2)\}ET2: {(ymax=3, x=3, Δx/Δy=−2)}
• ET3: ∅\mathrm{ET}3:\ \varnothingET3: ∅

活动边表 AET 的演化（给出每条扫描线开始时的 AET，及该线结束后的 xxx 更新结果）如下：

• 扫描线 y=1y=1y=1：插入 ET1\mathrm{ET}1ET1，
  AET(y=1)=(3,1,0),(2,1,2) \mathrm{AET}(y{=}1)=\big(3,1,0),(2,1,2)\\big AET(y=1)=(3,1,0),(2,1,2)
  更新到下一线（y=2y=2y=2）的交点：x:1→1x:1\to1x:1→1（第一条），x:1→3x:1\to3x:1→3（第二条）。
• 扫描线 y=2y=2y=2：先删除 ymax⁡=2y_{\max}=2ymax=2 的边（即 (2,3,2)(2,3,2)(2,3,2) 对应那条），再插入 ET2\mathrm{ET}2ET2，
  AET(y=2)=(3,1,0),(3,3,−2) \mathrm{AET}(y{=}2)=\big(3,1,0),(3,3,-2)\\big AET(y=2)=(3,1,0),(3,3,−2)
  更新到下一线（y=3y=3y=3）的交点：x:1→1x:1\to1x:1→1，x:3→1x:3\to1x:3→1。
• 扫描线 y=3y=3y=3：删除 ymax⁡=3y_{\max}=3ymax=3 的边后 AET=∅\mathrm{AET}=\varnothingAET=∅，算法结束。