机器学习基础知识

西瓜书的核心逻辑是 "模型→策略→算法" 三元组，所有机器学习方法都围绕这个框架展开，同时按假设空间、归纳偏好、监督/无监督/半监督/强化学习的脉络划分。

一、机器学习基础（第1章）

基本定义

机器学习：计算机基于数据构建概率统计模型，并运用模型对未知数据进行预测与分析的学科。
数据集：记录的集合，每条记录是一个示例/样本，样本的属性/特征构成特征向量，样本的结果称为标记。
标记空间：所有标记的集合，带标记的数据集用于监督学习，无标记的用于无监督学习。

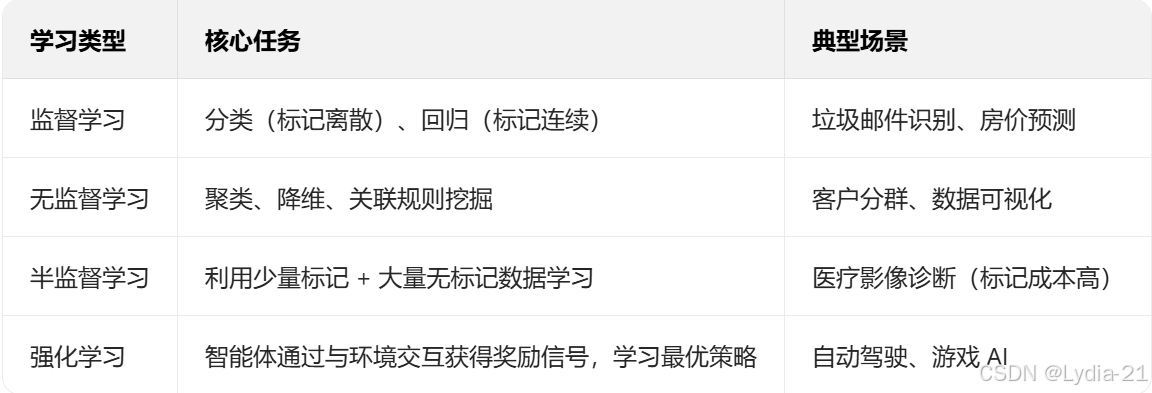
任务分类

关键概念

泛化能力：模型对未知数据的预测能力，是机器学习的核心目标。
归纳偏好：模型在假设空间中对假设的选择偏好，遵循 "奥卡姆剃刀" 原则（若多个假设与经验一致，选最简单的）。
NFL定理（没有免费的午餐）：所有算法的期望性能相同，脱离具体问题谈算法优劣无意义。

二、模型-策略-算法三元组（核心框架）

西瓜书的所有监督学习算法，都可拆解为这三个部分，是贯穿全书的主线。

模型：假设空间

模型是输入空间到输出空间的映射，对应假设空间中的一个假设。例如：线性回归的模型是 y=wTx+by = \boldsymbol{w}^T\boldsymbol{x}+by=wTx+b，假设空间是所有可能的参数 (w,b)(\boldsymbol{w},b)(w,b) 组合。

策略：损失函数与风险函数

损失函数：衡量单个样本预测值与真实值的差距，记为 L(y,f(x))L(y,f(\boldsymbol{x}))L(y,f(x))。常用损失函数：
- 0-1损失（分类）：L(y,f(x))={1,y≠f(x)0,y=f(x)L(y,f(\boldsymbol{x}))=\begin{cases}1, & y\neq f(\boldsymbol{x}) \\ 0, & y=f(\boldsymbol{x})\end{cases}L(y,f(x))={1,0,y=f(x)y=f(x)
- 平方损失（回归）：L(y,f(x))=(y−f(x))2L(y,f(\boldsymbol{x}))=(y-f(\boldsymbol{x}))^2L(y,f(x))=(y−f(x))2
- 对数损失（概率模型）：L(y,P(y∣x))=−log⁡P(y∣x)L(y,P(y|\boldsymbol{x}))=-\log P(y|\boldsymbol{x})L(y,P(y∣x))=−logP(y∣x)
风险函数：模型在整个样本空间上的期望损失，即 Rexp(f)=EP[L(y,f(x))]R_{exp}(f)=\mathbb{E}_{P}[L(y,f(\boldsymbol{x}))]Rexp(f)=EP[L(y,f(x))]。
经验风险：模型在训练集上的平均损失，即 Remp(f)=1N∑i=1NL(yi,f(xi))R_{emp}(f)=\frac{1}{N}\sum_{i=1}^N L(y_i,f(\boldsymbol{x}_i))Remp(f)=N1i=1∑NL(yi,f(xi))。
策略的目标：最小化风险函数，但真实风险无法计算，因此监督学习的策略分为两种：
1. 经验风险最小化（ERM）：直接最小化经验风险，适用于样本量足够大的场景（如线性回归）。
2. 结构风险最小化（SRM）：经验风险 + 正则化项，即 Rsrm(f)=Remp(f)+λJ(f)R_{srm}(f)=R_{emp}(f)+\lambda J(f)Rsrm(f)=Remp(f)+λJ(f)，用于缓解过拟合。

算法：求解最优模型的优化方法

算法是求解"最小化风险函数"这个优化问题的具体计算方法。例如：线性回归的算法是最小二乘法（解析解）或梯度下降法（数值解）；支持向量机的算法是序列最小最优化（SMO）。

三、监督学习（核心章节：第2-6章）

监督学习是西瓜书的重点，涵盖线性模型、决策树、支持向量机、贝叶斯分类器、集成学习等。

线性模型（第3章）

（1）线性回归

模型：y=wTx+by = \boldsymbol{w}^T\boldsymbol{x}+by=wTx+b
策略：经验风险最小化（平方损失）
算法：最小二乘法求解析解 w^=(XTX)−1XTy\hat{\boldsymbol{w}}=(\boldsymbol{X}^T\boldsymbol{X})^{-1}\boldsymbol{X}^T\boldsymbol{y}w^=(XTX)−1XTy；当 XTX\boldsymbol{X}^T\boldsymbol{X}XTX 不可逆时，用梯度下降法。

（2）对数几率回归（逻辑回归）

任务：二分类
模型：y=σ(wTx+b)y=\sigma(\boldsymbol{w}^T\boldsymbol{x}+b)y=σ(wTx+b)，其中 σ(⋅)\sigma(\cdot)σ(⋅) 是sigmoid函数（σ(z)=11+e−z\sigma(z)=\frac{1}{1+e^{-z}}σ(z)=1+e−z1），输出为样本属于正类的概率。
策略：极大似然估计（等价于最小化对数损失）
算法：梯度下降法、牛顿法。

（3）线性判别分析（LDA）

核心思想：投影后，同类样本的投影点尽可能近，异类样本的投影点尽可能远。
数学目标：最大化类间散度矩阵与类内散度矩阵的比值，即 J(w)=wTSbwwTSwwJ(\boldsymbol{w})=\frac{\boldsymbol{w}^T\boldsymbol{S}_b\boldsymbol{w}}{\boldsymbol{w}^T\boldsymbol{S}_w\boldsymbol{w}}J(w)=wTSwwwTSbw，其中 Sb\boldsymbol{S}_bSb 为类间散度矩阵，Sw\boldsymbol{S}_wSw 为类内散度矩阵。

决策树（第4章）

核心思想：递归划分特征空间，每个叶节点对应一个类别。
划分准则
- ID3：最大化信息增益，公式为 Gain(D,a)=Ent(D)−∑v=1V∣Dv∣∣D∣Ent(Dv)Gain(D,a)=Ent(D)-\sum_{v=1}^V \frac{|D^v|}{|D|}Ent(D^v)Gain(D,a)=Ent(D)−v=1∑V∣D∣∣Dv∣Ent(Dv)，其中 Ent(D)Ent(D)Ent(D) 为数据集D的熵（Ent(D)=−∑k=1Kpklog⁡2pkEnt(D)=-\sum_{k=1}^K p_k\log_2 p_kEnt(D)=−k=1∑Kpklog2pk），倾向于选择取值多的特征。
- C4.5：最大化信息增益率，公式为 Gain_ratio(D,a)=Gain(D,a)IV(a)Gain\ratio(D,a)=\frac{Gain(D,a)}{IV(a)}Gain_ratio(D,a)=IV(a)Gain(D,a)，其中 IV(a)IV(a)IV(a) 为特征a的固有值（IV(a)=−∑v=1V∣Dv∣∣D∣log⁡2∣Dv∣∣D∣IV(a)=-\sum{v=1}^V \frac{|D^v|}{|D|}\log_2 \frac{|D^v|}{|D|}IV(a)=−v=1∑V∣D∣∣Dv∣log2∣D∣∣Dv∣），克服ID3的偏好。
- CART：回归树用平方误差最小化（min⁡v[min⁡c1∑xi∈D1(v)(yi−c1)2+min⁡c2∑xi∈D2(v)(yi−c2)2]\min_{v}\left[\min_{c_1}\sum_{x_i\in D_1(v)}(y_i-c_1)^2 + \min_{c_2}\sum_{x_i\in D_2(v)}(y_i-c_2)^2\right]vmin c1minxi∈D1(v)∑(yi−c1)2+c2minxi∈D2(v)∑(yi−c2)2 ），分类树用基尼指数最小化（Gini(D)=1−∑k=1Kpk2Gini(D)=1-\sum_{k=1}^K p_k^2Gini(D)=1−k=1∑Kpk2）。
剪枝：解决过拟合，分为预剪枝（训练中提前停止划分）和后剪枝（生成完整树后剪去分支）。

支持向量机（SVM）（第6章）

（1）线性可分SVM

核心：寻找最大间隔超平面，满足约束条件 {wTx+b≥1,y=1wTx+b≤−1,y=−1\begin{cases}\boldsymbol{w}^T\boldsymbol{x}+b\ge 1, & y=1 \\ \boldsymbol{w}^T\boldsymbol{x}+b\le -1, & y=-1\end{cases}{wTx+b≥1,wTx+b≤−1,y=1y=−1。
优化目标：min⁡w,b12∥w∥2\min_{\boldsymbol{w},b}\frac{1}{2}\|\boldsymbol{w}\|^2w,bmin21∥w∥2，约束为 yi(wTxi+b)≥1y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b)\ge 1yi(wTxi+b)≥1（i=1,2,...,Ni=1,2,...,Ni=1,2,...,N）。
算法：拉格朗日对偶，将原问题转化为对偶问题求解，支持向量是满足 yi(wTxi+b)=1y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b)=1yi(wTxi+b)=1 的样本。

（2）线性不可分SVM

引入松弛变量 ξi≥0\xi_i \ge 0ξi≥0，允许部分样本不满足间隔约束，优化目标变为 min⁡w,b,ξi12∥w∥2+C∑i=1Nξi\min_{\boldsymbol{w},b,\xi_i}\frac{1}{2}\|\boldsymbol{w}\|^2 + C\sum_{i=1}^N\xi_iw,b,ξimin21∥w∥2+Ci=1∑Nξi，约束为 yi(wTxi+b)≥1−ξiy_i(\boldsymbol{w}^T\boldsymbol{x}_i+b)\ge 1-\xi_iyi(wTxi+b)≥1−ξi（i=1,2,...,Ni=1,2,...,Ni=1,2,...,N），其中 CCC 是惩罚系数（CCC 越大，对误分类样本惩罚越重）。

（3）非线性SVM

核心：引入核函数 k(xi,xj)=ϕ(xi)Tϕ(xj)k(\boldsymbol{x}_i,\boldsymbol{x}_j)=\phi(\boldsymbol{x}_i)^T\phi(\boldsymbol{x}_j)k(xi,xj)=ϕ(xi)Tϕ(xj)，将低维线性不可分数据映射到高维线性可分空间，无需显式计算映射函数 ϕ(⋅)\phi(\cdot)ϕ(⋅)。
常用核函数：
- 线性核：k(xi,xj)=xiTxjk(\boldsymbol{x}_i,\boldsymbol{x}_j)=\boldsymbol{x}_i^T\boldsymbol{x}_jk(xi,xj)=xiTxj
- 多项式核：k(xi,xj)=(γxiTxj+r)dk(\boldsymbol{x}_i,\boldsymbol{x}_j)=(\gamma\boldsymbol{x}_i^T\boldsymbol{x}_j + r)^dk(xi,xj)=(γxiTxj+r)d（γ,r,d\gamma,r,dγ,r,d 为超参数）
- 高斯核（RBF核）：k(xi,xj)=exp⁡(−γ∥xi−xj∥2)k(\boldsymbol{x}_i,\boldsymbol{x}_j)=\exp(-\gamma\|\boldsymbol{x}_i-\boldsymbol{x}_j\|^2)k(xi,xj)=exp(−γ∥xi−xj∥2)（γ>0\gamma>0γ>0 为超参数）
算法：序列最小最优化（SMO），将大优化问题分解为多个两个变量的小优化问题，降低计算复杂度。

贝叶斯分类器（第7章）

（1）贝叶斯定理

核心公式：P(c∣x)=P(x∣c)P(c)P(x)P(c|\boldsymbol{x})=\frac{P(\boldsymbol{x}|c)P(c)}{P(\boldsymbol{x})}P(c∣x)=P(x)P(x∣c)P(c)，其中 P(c)P(c)P(c) 为先验概率，P(x∣c)P(\boldsymbol{x}|c)P(x∣c) 为类条件概率，P(c∣x)P(c|\boldsymbol{x})P(c∣x) 为后验概率。

（2）朴素贝叶斯

假设：属性条件独立性，即 P(x∣c)=∏i=1dP(xi∣c)P(\boldsymbol{x}|c)=\prod_{i=1}^d P(x_i|c)P(x∣c)=i=1∏dP(xi∣c)（d为特征维度）。
策略：极大后验概率（MAP），分类时取 arg⁡max⁡cP(c∣x)\arg\max_c P(c|\boldsymbol{x})argcmaxP(c∣x)。
平滑技术：拉普拉斯平滑，解决零概率问题，公式为 P(xi∣c)=∣Dc,xi∣+1∣Dc∣+NiP(x_i|c)=\frac{|D_{c,x_i}|+1}{|D_c|+N_i}P(xi∣c)=∣Dc∣+Ni∣Dc,xi∣+1，其中 ∣Dc∣|D_c|∣Dc∣ 为类别c的样本数，∣Dc,xi∣|D_{c,x_i}|∣Dc,xi∣ 为类别c中特征xix_ixi的样本数，NiN_iNi 为特征xix_ixi的取值数。

（3）半朴素贝叶斯

放松属性独立性假设，如独依赖估计（ODE），假设每个属性仅依赖一个父属性，平衡模型复杂度和预测性能。

集成学习（第8章）

核心思想：组合多个弱学习器（性能略优于随机猜测的模型），形成强学习器，提升泛化能力。
Boosting
- 策略：串行生成弱学习器，每个弱学习器关注前一个模型的错误样本，通过调整样本权重（错误样本权重升高，正确样本权重降低）训练，最终加权组合弱学习器。
- 代表算法：AdaBoost，弱学习器权重由误差率决定（误差率越低，权重越高），最终预测结果为各弱学习器预测结果的加权投票。
- 进阶：梯度提升决策树（GBDT），基于残差学习，每一步训练一个决策树拟合前一步模型的预测残差（真实值-预测值），逐步降低损失。
Bagging
- 策略：并行生成弱学习器，通过自助采样（Bootstrap，有放回采样）生成不同的训练集，每个弱学习器独立训练，最终通过投票（分类）或平均（回归）得到结果。
- 代表算法：随机森林（RF），在Bagging基础上，决策树训练时随机选择部分特征进行划分，进一步降低模型方差，提升泛化能力。
模型融合：Stacking，将多个弱学习器的输出作为新特征，训练一个元学习器（如逻辑回归、SVM）做最终预测，融合效果更优但计算复杂度更高。

四、无监督学习（第9章）

聚类

基本概念：簇是样本的子集，满足簇内相似度高，簇间相似度低，核心是定义合适的距离/相似度度量。
距离度量：闵可夫斯基距离 distmk(xi,xj)=(∑u=1n∣xiu−xju∣p)1pdist_{mk}(\boldsymbol{x}i,\boldsymbol{x}j)=\left(\sum{u=1}^n |x{iu}-x_{ju}|^p\right)^{\frac{1}{p}}distmk(xi,xj)=(u=1∑n∣xiu−xju∣p)p1，其中p=1为曼哈顿距离，p=2为欧氏距离，p→∞为切比雪夫距离。
代表算法：
1. K-Means：划分式聚类，目标是最小化簇内平方和（min⁡∑k=1K∑x∈Ck∥x−μk∥2\min\sum_{k=1}^K\sum_{\boldsymbol{x}\in C_k}\|\boldsymbol{x}-\boldsymbol{\mu}_k\|^2mink=1∑Kx∈Ck∑∥x−μk∥2，μk\boldsymbol{\mu}_kμk 为第k个簇的质心），需预先指定k值，对初始质心敏感，常用K-Means++优化初始质心选择。
2. DBSCAN：密度聚类，基于核心对象、密度直达、密度可达定义簇（核心对象：邻域内样本数≥最小密度阈值；密度直达：核心对象与邻域内样本；密度可达：通过核心对象链连接），能发现任意形状的簇，无需指定k值，对噪声鲁棒。
3. 层次聚类：分为凝聚式（自底向上，从单个样本开始合并相似簇）和分裂式（自顶向下，从全样本开始拆分簇），最终形成聚类树，可根据需求选择簇数。

降维与度量学习

主成分分析（PCA）：线性降维，通过正交变换将特征映射到低维空间，保留方差最大的方向。目标是最大化投影方差（max⁡w1m∑i=1m(wTxi−wTxˉ)2\max_{\boldsymbol{w}}\frac{1}{m}\sum_{i=1}^m (\boldsymbol{w}^T\boldsymbol{x}_i-\boldsymbol{w}^T\bar{\boldsymbol{x}})^2wmaxm1i=1∑m(wTxi−wTxˉ)2，xˉ\bar{\boldsymbol{x}}xˉ 为样本均值），本质是求解协方差矩阵的特征值和特征向量，取前k个最大特征值对应的特征向量作为投影矩阵。
核PCA：非线性降维，用核函数将数据映射到高维特征空间，再在高维空间做PCA，适用于非线性数据。
流形学习：假设数据分布在低维流形上，通过保持样本局部邻域关系实现降维（如Isomap保持测地线距离，LLE保持局部线性关系），适用于非线性数据降维和可视化。

五、进阶内容（第10-16章）

特征选择与稀疏学习：特征选择分为过滤式（如相关系数、方差筛选）、包裹式（如递归特征消除）、嵌入式（如L1正则）；稀疏学习通过L1正则得到稀疏解（如Lasso回归），实现特征选择与模型训练一体化。
计算学习理论：研究机器学习的理论边界，如PAC学习（大概率近似正确），样本复杂度（训练模型所需最少样本数）、计算复杂度（训练模型所需计算资源），为模型选择和性能上限提供理论支撑。
半监督学习：利用未标记数据提升模型性能，分为生成式方法（假设数据服从某种生成模型，用未标记数据估计模型参数）、半监督SVM（通过间隔最大化利用未标记数据）、图半监督学习（将样本构建为图，利用图的平滑性传播标签）。
强化学习：核心是马尔可夫决策过程（MDP），包括状态S、动作A、奖励R、策略π、价值函数V；代表算法：动态规划（基于模型的规划方法）、蒙特卡洛方法（无模型，基于采样平均）、时序差分学习（结合动态规划和蒙特卡洛，在线学习）。
概率图模型：用图结构表示变量间的概率依赖关系，分为贝叶斯网络（有向图，如朴素贝叶斯、隐马尔可夫模型HMM）和马尔可夫随机场（无向图，如条件随机场CRF），适用于不确定性推理和序列建模。

六、关键补充（西瓜书强调的重难点）

过拟合与欠拟合

（1）过拟合（Overfitting）

西瓜书定义为：模型在训练集上误差极小、拟合效果优异，但在未见过的测试集上误差显著上升，泛化能力极差的现象。这是机器学习训练中最常见且需重点规避的问题。

核心原因：本质是模型复杂度超过数据本身的真实复杂度，模型不仅学习到了数据中的普遍规律，还将训练数据中的噪声、随机波动等非本质特征纳入学习范围，导致模型"死记硬背"训练数据，无法迁移到新样本。例如用10次多项式拟合仅含20个样本的线性数据，曲线会穿过所有训练点，但对新样本预测偏差极大。此外，训练样本量过少、样本分布不均衡也会加剧过拟合。

西瓜书核心解决方法：

正则化：在损失函数中加入模型复杂度惩罚项，限制参数规模，避免参数过度拟合噪声。分为L1正则（Lreg=Lemp+λ∑i=1d∣wi∣L_{reg}=L_{emp}+\lambda\sum_{i=1}^d|w_i|Lreg=Lemp+λi=1∑d∣wi∣）和L2正则（Lreg=Lemp+λ∑i=1dwi2L_{reg}=L_{emp}+\lambda\sum_{i=1}^d w_i^2Lreg=Lemp+λi=1∑dwi2），L1可使部分参数归零实现特征选择，L2使参数趋近于0，均能降低模型复杂度。
剪枝：针对决策树模型，分为预剪枝（训练中提前停止分支划分，如设定最小样本数阈值）和后剪枝（生成完整决策树后，移除泛化能力差的分支），本质是删减冗余决策节点，简化模型结构。
增大数据量：通过数据扩充（如图像旋转、文本同义词替换）或采集更多真实样本，让模型接触更全面的规律，减少噪声对模型的影响，这是最根本的解决方法之一。
早停：在模型训练过程中，实时监控验证集误差，当验证集误差连续多轮上升时，立即停止训练，避免模型在训练后期过度拟合训练数据。

（2）欠拟合（Underfitting）

西瓜书定义为：模型在训练集和测试集上的误差都较大，无法捕捉数据中的基本规律，拟合效果差的现象。

核心原因：模型复杂度低于数据真实复杂度，无法刻画数据中的非线性、高阶关联等特征。例如用线性模型拟合非线性数据（如房价与面积的二次关系），模型无法捕捉核心规律，导致训练和测试效果均不佳。此外，特征工程不足（如遗漏关键特征）也会引发欠拟合。

西瓜书核心解决方法：

增加模型复杂度：针对线性模型，可引入多项式特征（如x2、xyx^2、xyx2、xy）转化为非线性模型；针对树模型，可增加树的深度、叶子节点数；也可替换为更复杂的模型（如用GBDT替代单一决策树）。
强化特征工程：挖掘更多关键特征（如从用户行为数据中提取"活跃度"特征）、对特征进行非线性变换（如对数变换、归一化）、组合特征（如"年龄+职业"组合特征），为模型提供更丰富的信息，帮助模型捕捉规律。
模型评估与选择

（1）评估方法（数据集划分策略）

核心目标是通过合理划分数据集，客观评估模型泛化能力，避免因数据集划分不当导致的评估偏差。

留出法（Hold-out）：

原理：将数据集按比例（常用7:3或8:2）划分为互斥的训练集（用于模型训练）和测试集（用于评估泛化能力），单次划分后训练并评估模型。
西瓜书强调要点：划分时需保持数据分布一致性（如分类任务中正负样本比例与原数据集一致），避免因分布偏移导致评估失真；缺点是评估结果受划分方式影响大，稳定性差，可通过多次随机划分取平均值优化。

交叉验证法（Cross Validation）：

原理：将数据集随机划分为k个大小相近的互斥子集，每次用k-1个子集作为训练集，剩余1个子集作为测试集，重复k次（每次轮换测试集），最终取k次评估结果的平均值作为模型性能指标，即k折交叉验证。
西瓜书强调要点：k值常用5或10，兼顾评估稳定性和计算成本；极端情况为留一交叉验证（LOOCV），k等于样本数，评估结果最稳定但计算量极大，适用于样本量极少的场景；交叉验证能充分利用数据，评估结果更可靠，是工业界和科研中最常用的方法。

自助法（Bootstrap）：

原理：基于自助采样（有放回采样），从含m个样本的数据集D中，随机采样m次得到训练集D'（部分样本重复，部分样本未被选中），未被选中的样本（约36.8%）作为测试集，重复该过程多次，取评估结果平均值。
西瓜书强调要点：适用于样本量极小、难以划分训练/测试集的场景；优点是能充分利用数据，缺点是改变了原数据集的分布，可能导致评估结果有偏差，对分类任务影响较小，对回归任务适用性较弱。

（2）性能度量（模型效果量化指标）

根据任务类型（分类/回归）选择对应指标，客观反映模型预测能力。

① 分类任务指标（针对离散标签预测）

准确率（Accuracy）：Accuracy=TP+TNTP+TN+FP+FNAccuracy = \frac{TP+TN}{TP+TN+FP+FN}Accuracy=TP+TN+FP+FNTP+TN，预测正确的样本数占总样本数的比例，适用于正负样本均衡的场景；缺点是对不均衡数据敏感（如负样本占90%，模型全预测为负也能达到90%准确率）。
精确率（Precision）与召回率（Recall）：精确率P=TPTP+FPP = \frac{TP}{TP+FP}P=TP+FPTP，预测为正类的样本中真实为正类的比例（避免误判正类）；召回率R=TPTP+FNR = \frac{TP}{TP+FN}R=TP+FNTP，真实为正类的样本中被正确预测的比例（避免漏判正类）。二者存在trade-off，需根据场景取舍（如垃圾邮件识别优先精确率，疾病诊断优先召回率）。
F1分数：F1=2×P×RP+RF1 = 2\times\frac{P\times R}{P+R}F1=2×P+RP×R，精确率和召回率的调和平均数，综合二者性能，避免单一指标的局限性。
ROC曲线与AUC值：ROC曲线以假正例率（FPR=FPTN+FP\frac{FP}{TN+FP}TN+FPFP）为横轴、真正例率（TPR=TPTP+FN\frac{TP}{TP+FN}TP+FNTP）为纵轴，反映模型在不同阈值下的分类性能；AUC是ROC曲线下的面积，取值范围[0.5,1]，AUC越接近1，模型分类能力越强，适用于二分类和多分类任务，对不均衡数据不敏感。

② 回归任务指标（针对连续标签预测）

均方误差（MSE）：MSE=1m∑i=1m(yi−y^i)2MSE = \frac{1}{m}\sum_{i=1}^m (y_i - \hat{y}_i)^2MSE=m1i=1∑m(yi−y^i)2，预测值与真实值差值的平方和均值，对异常值敏感（异常值平方后放大影响）。
平均绝对误差（MAE）：MAE=1m∑i=1m∣yi−y^i∣MAE = \frac{1}{m}\sum_{i=1}^m |y_i - \hat{y}_i|MAE=m1i=1∑m∣yi−y^i∣，预测值与真实值绝对差值的均值，对异常值鲁棒性更强，反映误差的平均水平。
决定系数（R2R^2R2）：R2=1−∑i=1m(yi−y^i)2∑i=1m(yi−yˉ)2R^2 = 1 - \frac{\sum_{i=1}^m (y_i - \hat{y}i)^2}{\sum{i=1}^m (y_i - \bar{y})^2}R2=1−∑i=1m(yi−yˉ)2∑i=1m(yi−y^i)2，其中yˉ\bar{y}yˉ为真实值的均值，反映模型对数据变异的解释能力，取值范围(-∞,1]，R2R^2R2越接近1，模型拟合效果越好。