算法刷题--字符串

一起努力啊～2026-01-19 10:04

文章目录

    • [1、344 反转字符串](#1、344 反转字符串)
    • [2、541 反转字符串②](#2、541 反转字符串②)
    • 3、替换数字
    • [4、151 翻转字符串里的单词](#4、151 翻转字符串里的单词)
    • 5、右旋转字符串
    • [6、28 找出字符串中第一个匹配项的下标](#6、28 找出字符串中第一个匹配项的下标)
    • kmp算法详解
      • [1. 核心原理：最长相等前后缀](#1. 核心原理：最长相等前后缀)
      • [2. 构建 `next` 数组](#2. 构建 next 数组)
      • [3. KMP 匹配过程](#3. KMP 匹配过程)
      • [4. C 语言代码实现](#4. C 语言代码实现)
      • [5. 为什么 KMP 很快？](#5. 为什么 KMP 很快？)
      • [理解 KMP 的一个小技巧](#理解 KMP 的一个小技巧)
      • [第一步：计算 `next` 数组（核心：找最长相等前后缀）](#第一步：计算 next 数组（核心：找最长相等前后缀）)
      • 第二步：模拟匹配过程
        • [1. 顺利匹配阶段](#1. 顺利匹配阶段)
        • [2. 冲突发生（关键时刻！）](#2. 冲突发生（关键时刻！）)
        • [3. 利用 `next` 数组"瞬移"](#3. 利用 next 数组“瞬移”)
        • [4. 继续匹配](#4. 继续匹配)
      • [总结 KMP 的精髓](#总结 KMP 的精髓)
      • 学习建议
    • [7、459 重复的子字符串](#7、459 重复的子字符串)

1、344 反转字符串

题目

代码

使用双指针

c 复制代码 
void reverseString(char* s, int sSize) {
    int len = sSize;
    int left = 0;
    int right = len-1;
    char tmp = 0;
    while(right > left){
        tmp = s[left];
        s[left] = s[right];
        s[right] = tmp;
        left++;
        right--;
    }
}

时间复杂度：O(n)

空间复杂度：O(1)

2、541 反转字符串②

题目

代码

c 复制代码 
char* reverseStr(char* s, int k) {
    int len = strlen(s);
    int left;
    int right;
    char tmp;
    int count = 0;
    int start = 0;
    while((len - start) >= 2*k){
        left = start;
        right = left+k-1;
        while (right > left) {
            tmp = s[left];
            s[left] = s[right];
            s[right] = tmp;
            right--;
            left++;
        }
        count++;
        start += 2*k;
    }
    if(k <= (len-start) && (len-start) < 2*k) {
        left = start;
        right = left+k-1;
        while (right > left) {
            tmp = s[left];
            s[left] = s[right];
            s[right] = tmp;
            right--;
            left++;
        }
    }
    if ((len-start) < k) {
        left = start;
        right = len-1;
        while (right > left) {
            tmp = s[left];
            s[left] = s[right];
            s[right] = tmp;
            right--;
            left++;
        }
    } 
    return s;
}

时间复杂度：O(n)

空间复杂度：O(1)

优化版

c 复制代码 
char* reverseStr(char* s, int k) {
    int len = strlen(s);
    for(int i = 0;i < len;i += 2*k){
        int left = i;
        int right = (i+k-1 < len)?i+k-1:len-1;
        while(right>left){
            char tmp = s[left];
            s[left] = s[right];
            s[right] = tmp;
            right--;
            left++;
        }
    }
    return s;
}

时间复杂度：O(n)

空间复杂度：O(1)

3、替换数字

题目

代码

c 复制代码 
#include <stdlib.h>
#include <stdio.h>
#include <string.h>
#include <ctype.h>
int main(){
    char s[10000];
    scanf("%s",s);

    int old_len = strlen(s);
    int new_len = 0;
    for(int i = 0;i < old_len;i++){
        if(isdigit(s[i])){
            new_len+=6;
        }else{
            new_len+=1;
        }
    }
    
    char* res = (char*)malloc(sizeof(char)*(new_len+1));
    int a = 0;
    for(int i = 0;i < old_len;i++){
        if(isdigit(s[i])){
            res[a++] = 'n';
            res[a++] = 'u';
            res[a++] = 'm';
            res[a++] = 'b';
            res[a++] = 'e';
            res[a++] = 'r';
        }else{
            res[a++] = s[i];
        }
    }
    s[new_len] = '\0';
    printf("%s",res);
    free(res);
    res = NULL;
    return 0;
}

时间复杂度：O(n)

空间复杂度：O(n）

4、151 翻转字符串里的单词

题目

代码

有点难度，核心思路是先去除多余的空格，再反转s，然后再反转每个单词。

c 复制代码 
void reverse(char* s,int start,int end){
    for(int i = start,j = end;i < j;i++,j--){
        int tmp = s[i];
        s[i] = s[j];
        s[j] = tmp;
    }
}

void del_extraspace(char* s){
    int start = 0;
    int end = strlen(s)-1;
    while(s[start] == ' '){
        start++;
    }
    while(s[end] == ' '){
        end--;
    }
    int slow = 0;
    for(int i = start;i <= end;i++){
        if(s[i] == ' ' && s[i+1] == ' '){
            continue;
        }else{
            s[slow++] = s[i];
        }
    }
    s[slow] = '\0';
}

char* reverseWords(char* s) {
    del_extraspace(s);
    reverse(s,0,strlen(s)-1);
    int slow = 0;
    for(int i = 0;i <= strlen(s);i++){
        if(s[i] == ' ' || s[i] == '\0'){
            reverse(s,slow,i-1);
            slow = i+1;
        }
    }
    return s;
}

代码详解~

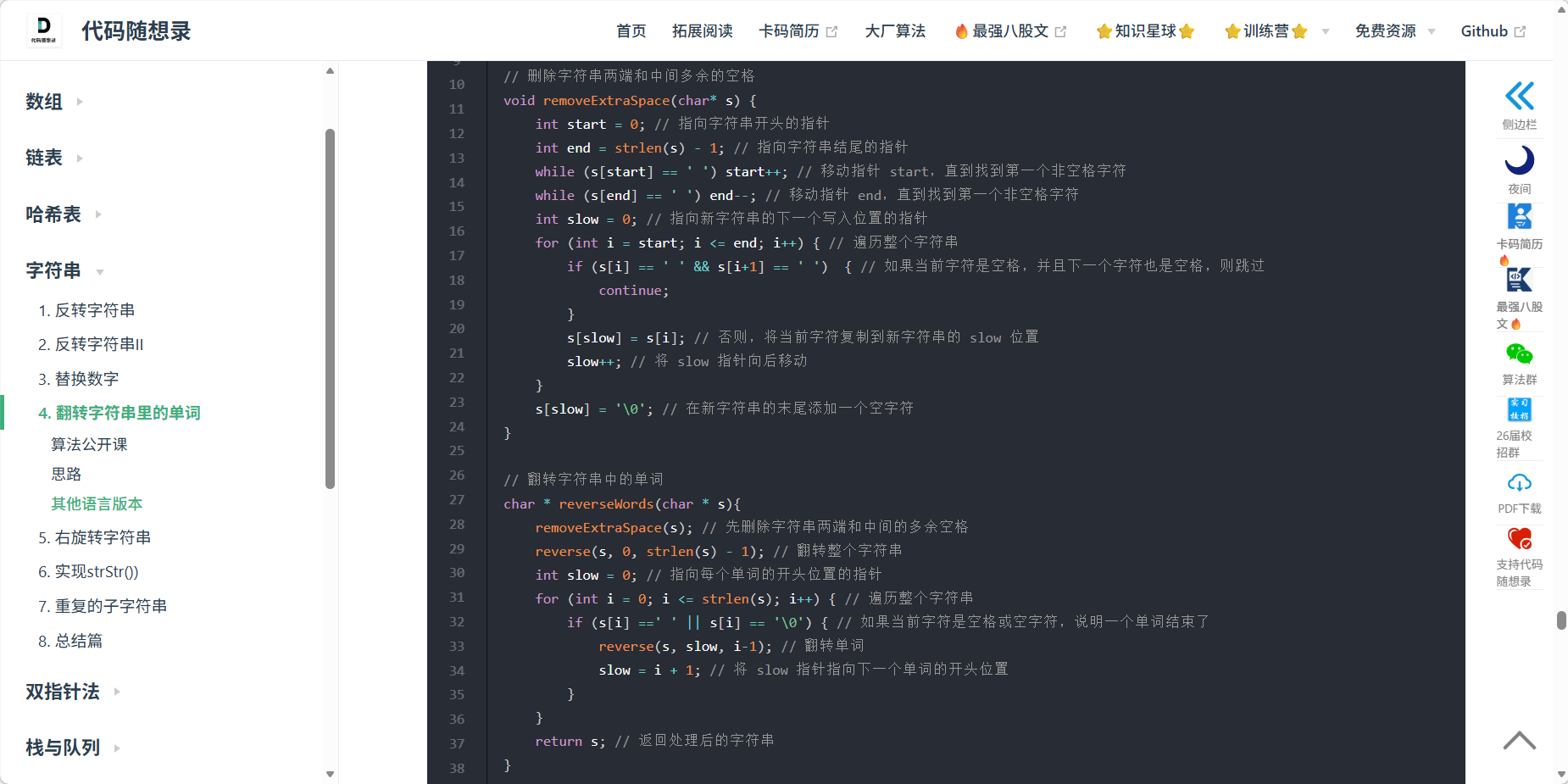
时间复杂度：O(n)

空间复杂度：O(1)

5、右旋转字符串

题目

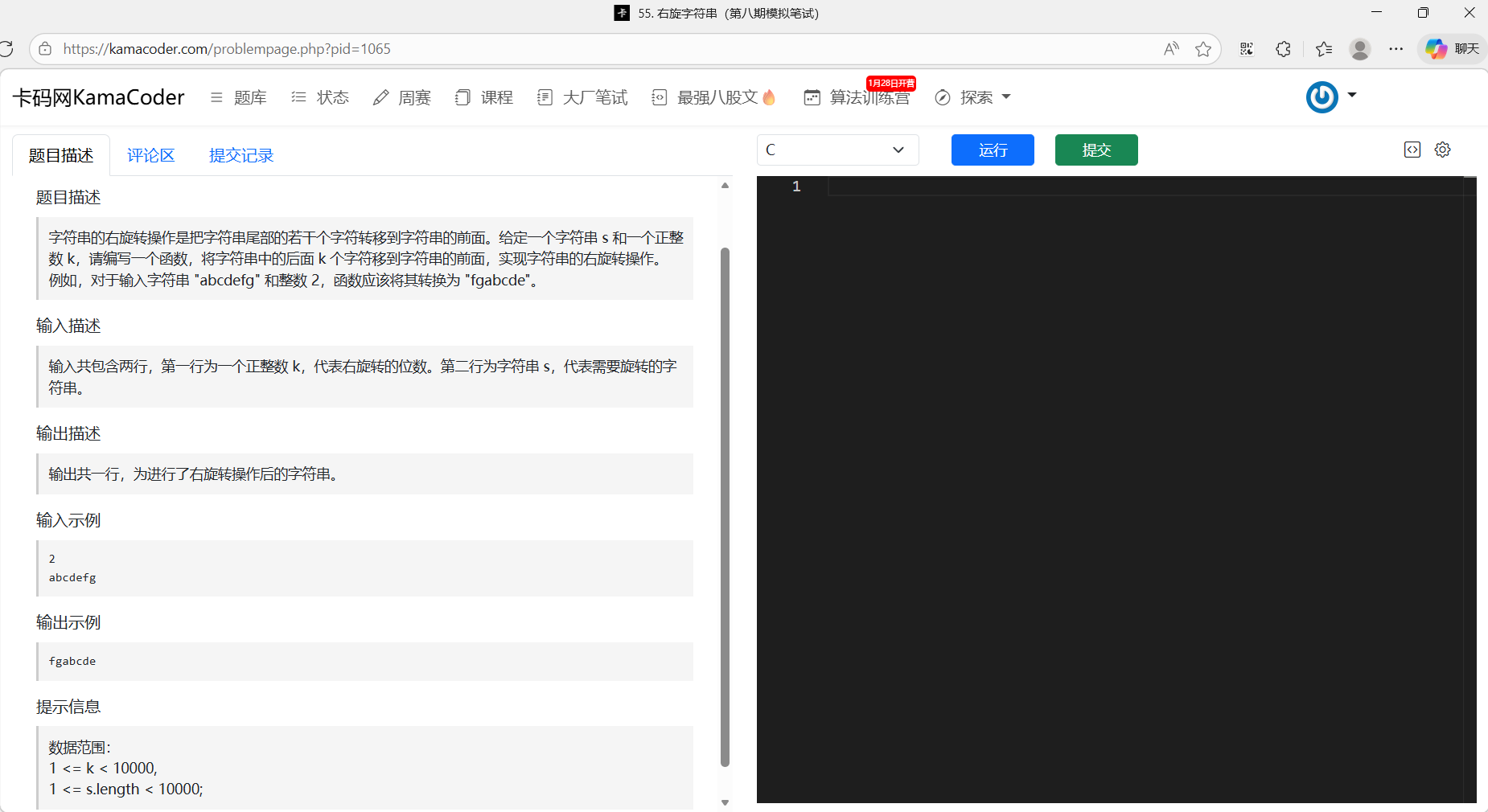
代码

思路：将字符串分为n-k，k两个子串，然后反转字符串，再分别反转两个子串。

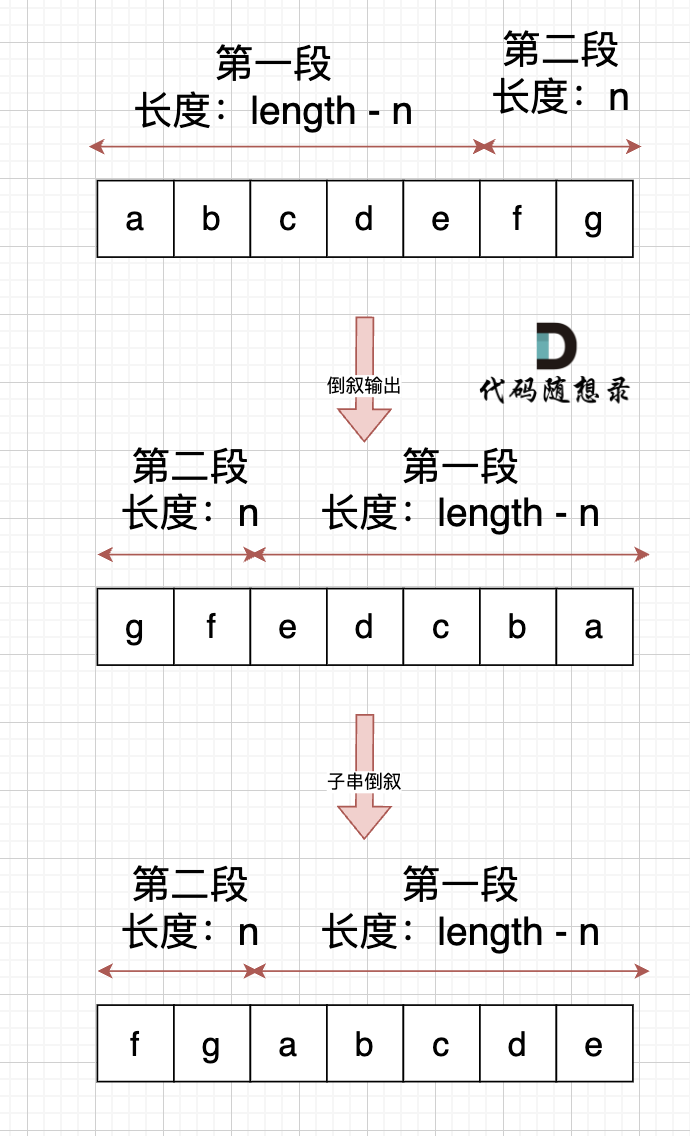
c 复制代码 
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
void reverse(char* s,int start,int end){
    for(int i = start,j = end;i < j;i++,j--){
        int tmp = s[i];
        s[i] = s[j];
        s[j] = tmp;
    }
}
int main(){
    char s[10001];
    int k = 0;
    scanf("%d\n",&k);
    scanf("%s",s);
    reverse(s,0,strlen(s)-1);
    reverse(s,0,k-1);
    reverse(s,k,strlen(s)-1);
    printf("%s",s);
    return 0;
}

会了上一题，这道题简直是易如反掌嘻嘻

时间复杂度：O(n)

空间复杂度：O(1)

6、28 找出字符串中第一个匹配项的下标

题目

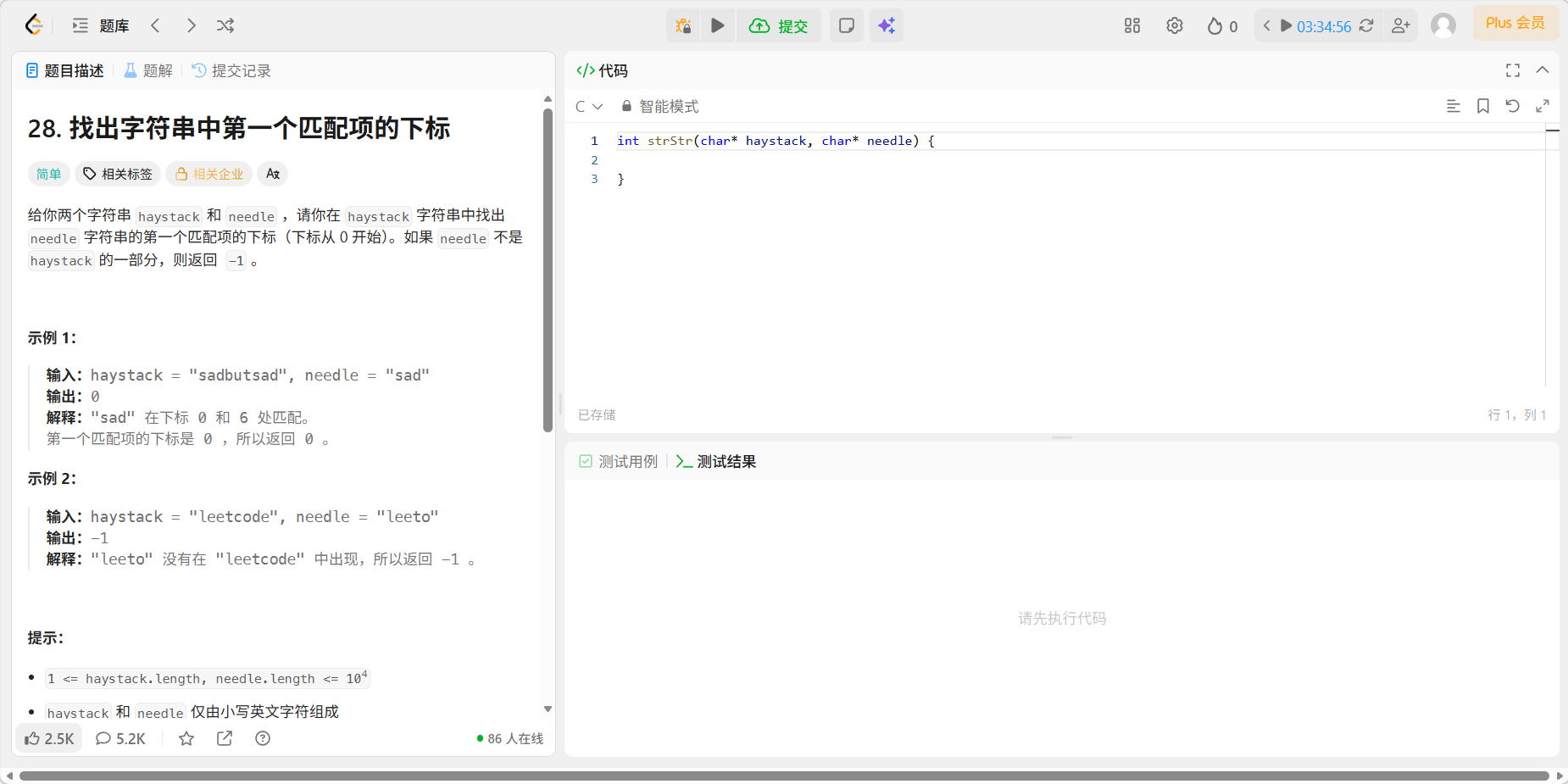
代码

直接暴力解了想到了kmp但是不会写代码哩

c 复制代码 
int strStr(char* haystack, char* needle) {
    int a = strlen(haystack);
    int b = strlen(needle);
    if(a < b){
        return -1;
    }
    for(int i = 0;i < a;i++){
        int b1 = 0;
        int a1 = i;
        while(b1 < b){
            if(haystack[a1] == needle[b1]){
                b1++;
                a1++;
            }else{
                break;
            }
        }
        if(b1==b){
            return i;
        }
    }
    return -1;
}

时间复杂度：O(n*m)，n是haystack的长度，m是needle的长度。

空间复杂度：O(1)

kmp算法详解

力扣第 28 题（找出字符串中第一个匹配项的下标）是学习 KMP 算法 的经典入门题。

KMP 的核心思想是：当出现字符不匹配时，利用已经匹配过的信息，尽量减少模式串（needle）的回退幅度，从而避免主串（haystack）指针的回溯。

1. 核心原理：最长相等前后缀

KMP 算法的关键在于构建一个 next 数组（也叫 LPS 数组，Longest Prefix which is also Suffix）。

  • 前缀：包含第一个字符，但不包含最后一个字符的子串。
  • 后缀：包含最后一个字符，但不包含第一个字符的子串。

例子 ：对于模式串 "ABABC"

  • 子串 "A"：前后缀为空，长度 0。
  • 子串 "AB"：前缀 A，后缀 B，相等长度 0。
  • 子串 "ABA"：前缀 A, AB，后缀 A, BA。相等的只有 A，长度 1。
  • 子串 "ABAB"：前缀 A, AB, ABA，后缀 B, AB, BAB。相等的是 AB，长度 2。

2. 构建 next 数组

next[i] 表示在模式串的前 i + 1 i+1 i+1 个字符构成的子串中，最长相等前后缀的长度。

构建逻辑：

  1. 使用两个指针：i（指向后缀末尾）和 j（指向前缀末尾，也代表当前相等前后缀的长度）。
  2. 如果 needle[i] == needle[j]，则 j++，记录 next[i] = j。
  3. 如果 needle[i] != needle[j]，则 j 要回退到 next[j-1]，直到相等或 j 回到 0。

3. KMP 匹配过程

假设我们在 haystack 中寻找 needle：

  1. 当 haystack[i] == needle[j] 时，两个指针同时后移。
  2. 当 haystack[i] != needle[j] 时：
  • 普通暴力法 ：i 回溯到开始的下一个位置，j 回到 0。
  • KMP 法 ：i 不动 ，j 直接跳到 next[j-1] 的位置继续匹配。

4. C 语言代码实现

gimini老师版（个人觉得这版更好懂些所以放前面了嘿嘿）

c 复制代码 
void getNext(int* next,char* s){
    int j = 0;
    next[0] = 0;
    for(int i = 1;s[i] != '\0';i++){
        //1、不匹配时，j后退
        while(j > 0 && s[i] != s[j]){
            j = next[j-1];
        }
        //2、匹配时，j增加
        if(s[i] == s[j]){
            j++;
        }
        //3、更新next数组
        next[i] = j;
    }
}

int strStr(char* haystack,char* needle){
    int n = strlen(haystack),m = strlen(needle);
    if(m == 0) return 0;

    int* next = (int*)malloc(sizeof(int)*m);
    getNext(next,needle);

    int j = 0;//needle的指针
    for(int i = 0;i < n;i++){//haystack的指针i永远不回头
        while(j > 0 && haystack[i] != needle[j]){
            j = next[j-1];//寻找之前匹配过的位置
        }
        if(haystack[i] == needle[j]){
            j++;
        }
        if(j == m){//完全匹配
            free(next);
            return i - m + 1;
        }
    }
    free(next);
    return -1;
}

代码随想录版

c 复制代码 
int *build_next(char* needle,int len){
    int *next = (int*)malloc(len * sizeof(int));
    assert(next);//确保分配成功

    //初始化next数组
    next[0] = -1;//next[0]设置为-1，表示没有有效前缀匹配
    if(len <= -1){//如果模式串长度小于等于1，直接返回
        return next;

    }
    next[1] = 0;//next[1]设置为0，表示第一个字符没有公共前后缀

    //构建next数组，i从模式串的第三个字符开始，j指向当前匹配的最长前缀长度
    int i = 2,j = 0;
    while(i < len){
        if(needle[i-1] == needle[j]){
            j++;
            next[i] = j;
            i++;
        }else if(j > 0){
            //如果不匹配且j > 00,回退到次长匹配前缀的长度
            j = next[j];
        }else{
            next[i] = 0;
            i++;
        }
    }
    return next;
}
int strStr(char* haystack, char* needle) {
    int needle_len = strlen(needle);
    int haystack_len = strlen(haystack);

    int *next = build_next(needle,needle_len);

    int i = 0,j = 0;//i指向主串的当前起始位置，j指向模式串的当前匹配位置
    while(i <= haystack_len - needle_len){
        if(haystack[i+j] == needle[j]){
            j++;
            if(j == needle_len){
                free(next);
                next = NULL;
                return i;
            }
        }else{
            i += j - next[j];//调整主串的起始位置
            j = j > 0 ? next[j] : 0;
        }
    }
    free(next);
    next = NULL;
    return -1;
}

时间复杂度：O(n+m)，n是haystack的长度，m是needle的长度。

空间复杂度：O(m)

5. 为什么 KMP 很快？

  • 时间复杂度 ：。主串指针 i 从头到尾只走一遍，不会回头。
  • 空间复杂度 ：。需要额外的 next 数组存储模式串的信息。

理解 KMP 的一个小技巧

你可以把 next 数组想象成一个**"搜索引擎的智能提示"**。当你输入到一半发现输错了（不匹配），KMP 告诉你：虽然这个词不对，但你刚才输入的后半部分，正好是另一个可能正确的词的开头，所以你不用从头再输入。

接下来，我们就用具体的例子：haystack = "aabaabaaf" ，needle = "aabaaf"，手把手拆解一遍 KMP 的执行过程。

第一步：计算 next 数组（核心：找最长相等前后缀）

对 needle = "aabaaf" 计算其各子串的最长相等前后缀长度：

子串 前缀 后缀 相等长度 next 值
a 无 无 0 next[0] = 0
aa a a 1 next[1] = 1
aab a, aa b, ab 0 next[2] = 0
aaba a, aa, aab a, ba, aba 1 next[3] = 1
aabaa a, aa, aab, aaba a, aa, baa, abaa 2 next[4] = 2
aabaaf 无匹配 无匹配 0 next[5] = 0

最终 next 数组为：[0, 1, 0, 1, 2, 0]。

第二步：模拟匹配过程

现在让 i 扫描 haystack，j 扫描 needle。

1. 顺利匹配阶段

当 i 从 0 到 4 时，haystack[i] 和 needle[j] 完全一样。

  • 此时：i = 4, j = 4，匹配了 "aabaa"。
2. 冲突发生（关键时刻！）

当 i = 5 时：

  • haystack[5] 是 'b'
  • needle[5] 是 'f'
  • 不匹配了！
3. 利用 next 数组"瞬移"

此时如果用暴力法，i 就要回退到 1，j 回到 0，从 "aba..." 重新开始比。
KMP 的做法：

  • i 绝对不后退 ，依然停在 5（字符 'b'）。
  • j 查看它前一个字符的 next 值，即 next[j-1] next[4]。
  • 我们查表发现 next[4] = 2。
  • 于是 j 直接跳到索引 2 的位置（字符 'b'）。

为什么跳到 2？ 因为 next[4]=2 意味着前面匹配成功的 "aabaa" 中，头尾都有长度为 2 的 "aa"。既然尾巴的 "aa" 已经匹配过了，那我就默认头部的 "aa" 也匹配好了，直接从第三个字符 'b' 开始比。

4. 继续匹配
  • 此时 i = 5 是 'b'，j = 2 也是 'b'。
  • 匹配成功！i 和 j 同时后移。
  • 接下来直到 needle 结束都会匹配成功。

总结 KMP 的精髓

  1. i 不回头：主串的指针就像时间一样只管往前走。
  2. j 找前人 ：当 j 走不通时，它不回起点，而是问 next 数组："我之前匹配过的这一段里，有没有哪一截开头跟我的结尾长得一样？"
  3. 节省时间：通过这种"瞬移"，我们跳过了大量绝对不可能匹配成功的起始位置。

学习建议

如果你现在还有点懵，这非常正常。建议你在纸上画两个纸条（haystack 和 needle），手动根据 next 指针平移 needle 的纸条。当你看到 needle 纸条**"啪"地一下向右滑动一段距离，而 i 指针却能接着往下指**的时候，你就彻底悟了。

7、459 重复的子字符串

题目

代码

这题是字符串算法中的经典题。它的目标是判断一个字符串是否可以由它的一个子串重复多次构成。

1. 暴力解法 (Brute Force)

思路：

如果一个字符串 S 是由重复子串构成的，那么这个重复子串的长度 i 一定能被总长度 n 整除。而且，i 的取值范围是从 1 到 n/2。

步骤：

  1. 遍历子串可能的长度 i（从 1 到 n/2）。
  2. 如果 n 能被 i 整除，说明长度为 i 的子串可能是重复单元。
  3. 取出前 i 个字符作为模板，将它与后面每隔 i 长度的子串进行比较。
  4. 如果所有分段都和模板一致，返回 true。

代码：

c 复制代码 
bool repeatedSubstringPattern(char* s) {
    int n = strlen(s);
    for (int i = 1; i <= n / 2; i++) {
        if (n % i == 0) {
            bool match = true;
            for (int j = i; j < n; j++) {
                if (s[j] != s[j - i]){
                    match = false;
                    break;
                }
            }
            if(match){
                return true;
            }
        }
    }
    return false;
}

复杂度：

  • 时间： O ( n 2 ) O(n^2) O(n2)（外层循环 n / 2 n/2 n/2 次，内层字符串比较最坏 O ( n ) O(n) O(n)）。
  • 空间： O ( 1 ) O(1) O(1)。

2. 移动匹配 (String Concatenation)

这是一个非常巧妙的数学直觉解法。

思路：

假设字符串 s 由重复子串 k 构成（即 s = kkk ）。

如果我们把两个 s 拼接在一起形成 S ′ = s + s S' = s + s S′=s+s，那么 S ′ S' S′内部一定包含多个 s 。

具体的，原本的 s+s 是 [kkk][kkk]。如果我们破坏掉第一个 s 的开头和第二个 s 的结尾，中间剩下的部分依然会拼凑出至少一个完整的 s 。

步骤：

  1. 将两个 s 拼接：char* double_s = s + s。
  2. 掐头去尾：删除第一个字符和最后一个字符。
  3. 在剩下的字符串中查找是否包含原字符串 s 。
  4. 如果能找到，说明 s 是由重复子串构成的。

代码：

c 复制代码 
bool repeatedSubstringPattern(char* s) {
    int n = strlen(s);
    if(n <= 1){
        return false;
    }
    char* double_s = (char*)malloc(sizeof(char)*(2*n+1));
    strcpy(double_s,s);
    strcat(double_s,s);
    // memcpy(double_s,s,n);
    // memcpy(double_s+n,s,n+1);
    double_s[2*n-1] = '\0';
    bool result = strstr(double_s+1,s) != NULL;
    free(double_s);
    return result;
}
第一阶段：空间准备
c 复制代码 
int n = strlen(s);
if (n <= 1) return false; // 单个字符显然不符合由"子串"重复多次的定义

char* double_s = (char*)malloc(sizeof(char) * (2 * n + 1));
strcpy(double_s, s);
strcat(double_s, s);

语法功能拆解

c 复制代码 
 strcpy(double_s, s); (String Copy)

  • 作用：把源字符串 s 的内容（包括结束符 \0）拷贝到目标地址 double_s 中。

  • 状态：此时 double_s 的内容和 s 完全一样。

c 复制代码 
 strcat(double_s, s); (String Concatenate)

  • 作用：把源字符串 s 的内容追加到 double_s 的末尾。

  • 过程：它会先找到 double_s 目前的结束符 \0，然后从那个位置开始覆盖写入 s 的内容，最后再补一个 \0。

  • 这里创建了一个两倍长度的字符串。如果 ，那么 double_s 现在就是 "abcabc"。

性能小贴士

  • 在处理非常长的字符串时，strcat 有一个性能缺陷：它每次都要从头遍历一遍字符串来寻找 \0。

  • 更高效的替代方案： 如果你追求极致性能，可以使用 memcpy，因为你已经知道 s 的长度 n，可以直接精准定位：

c 复制代码 
memcpy(double_s, s, n);          // 拷贝第一段
memcpy(double_s + n, s, n + 1);  // 拷贝第二段（连同 \0 一起拷贝）

这样就不需要像 strcat 那样去扫描字符串寻找结尾，速度会更快。

第二阶段：掐头去尾
c 复制代码 
double_s[2 * n - 1] = '\0';
  • 2 * n - 1 是拼接后字符串的最后一个字符的下标。
  • 将其设为 \0（字符串结束符），意味着我们切断了末尾。
  • 注意：开头的去除是在下一步通过指针移动实现的。
第三阶段：中间匹配
c 复制代码 
bool result = strstr(double_s + 1, s) != NULL;
  • double_s + 1 ：这是精髓。指针向右移动一位，相当于去掉了第一个字符。
  • strstr(A, B)：在 A 中查找 B。
  • 逻辑 ：如果在去掉头尾的 double_s 中还能找到原字符串 s，说明 s 具有周期性。

strstr(str1, str2) 函数的作用是在 str1 中查找是否包含子串 str2。

  • 如果找到了：返回指向 str1 中第一次出现 str2 位置的指针。

  • 如果没找到：返回 NULL。

所以，strstr(double_s + 1, s) != NULL 的意思是："在去掉了头的双倍字符串中，寻找原字符串 s。只要能找到，结果就是真。"

实例模拟（为什么这个方法有效？）

情况 A： 是重复的（如 "abab"）
  1. s + s = "abababab"
  2. 掐头去尾 = " (b)ababab(a) " 剩下的中间部分是 "bababa"。
  3. 在 "bababa" 中查找 "abab"？
  • 索引 1 位置：b [abab] a 找到了！ 返回 true。
情况 B： 不是重复的（如 "aba"）
  1. s + s = "abaaba"
  2. 掐头去尾 = " (b)aaba(a) " 剩下的中间部分是 "aaba"。
  3. 在 "aaba" 中查找 "aba"？
  • 索引 0 位置：aab... (不匹配)
  • 索引 1 位置：aba... (匹配) ------ 等等！ * 注意： 在情况 B 中，strstr 会找到第二个原字符串的残余部分，但因为我们已经把最后一个字符切掉了，所以它找不全。除非 s 本身有内部周期。
  • 实验结果：在 "aaba" 中找 "aba"，由于末尾被切，只能找到 "aab"。查找失败，返回 false。

复杂度：

  • 时间： O ( n ) O(n) O(n) (取决于底层 strstr 的实现)。
  • 空间： O ( n ) O(n) O(n) (需要存储拼接后的字符串)。

3. KMP 算法解法

这是该题最高效、也最能体现 KMP 算法精髓的解法。

核心结论：

如果一个长度为 n 的字符串是由重复子串构成的，那么：

  1. 它最长相等前后缀的长度 L = n e x t [ n − 1 ] L = next[n-1] L=next[n−1]（这里指长度，不是索引）。
  2. 如果 n 能够被 ( n − L ) (n - L) (n−L) 整除，那么这个字符串一定由重复子串构成。
  3. 且那个重复的子串长度就是 ( n − L ) (n - L) (n−L) 。

思路分析：

  • next[n-1] 记录了整个字符串中最长的相等前后缀。
  • 如果有重复单元，前后缀重合后，剩下的那一部分 n - next[n-1] 恰好就是最小的重复单元。
  • 例子 ：s = "ababab"， n = 6 n=6 n=6。
  • next 数组最后一位的值是 4（相等前后缀是 "abab"）。
  • n − L = 6 − 4 = 2 n - L = 6 - 4 = 2 n−L=6−4=2。
  • 6可以被 2 整除，所以是重复的，且重复单元长度为 2（即 "ab"）。

步骤：

  1. 计算字符串 s 的 next 数组。
  2. 获取数组最后一位的值 L。
  3. 判断条件：L > 0（必须有前后缀重合）且 n % (n - L) == 0。

代码：

c 复制代码 
bool repeatedSubstringPattern(char* s) {
    int n = strlen(s);
    if (n <= 1) return false;

    // 构建 next 数组（存储最长相等前后缀长度）
    int* next = (int*)malloc(sizeof(int) * n);
    next[0] = 0;
    int j = 0;

    for (int i = 1; i < n; i++) {
        while (j > 0 && s[i] != s[j]) {
            j = next[j - 1];
        }
        if (s[i] == s[j]) {
            j++;
        }
        next[i] = j;
    }

    // 最后一位的 next 值即为整个字符串的最长相等前后缀长度 L
    int L = next[n - 1];
    free(next);

    // 核心判断：
    // 1. L > 0 表示存在公共前后缀
    // 2. n % (n - L) == 0 表示剩下的部分正好能被整除
    return L > 0 && (n % (n - L) == 0);
}

复杂度：

  • 时间： O ( n ) O(n) O(n)（只需一次 KMP next 数组构建）。
  • 空间： O ( n ) O(n) O(n)（存储 next 数组）。

总结比较

方法 核心思想 优点 缺点
暴力解 逐一尝试可能的长度 极其直观，不依赖高级算法 时间复杂度高
移动匹配 s s s 在 ( s + s ) [ 1 : − 1 ] (s+s)[1:-1] (s+s)[1:−1] 中出现 代码极简，思维跳跃 空间开销大，依赖字符串匹配库
KMP 利用最长前后缀余数 效率最高，面试加分项 理解难度最大
相关推荐
独断万古他化2 小时前
【二分算法 深度解析】二段性思维与经典题型全通关
java·算法
啊阿狸不会拉杆2 小时前
《数字图像处理》第 10 章 - 图像分割
图像处理·人工智能·深度学习·算法·计算机视觉·数字图像处理
早川9192 小时前
9种常用排序算法总结
数据结构·算法·排序算法
Yupureki2 小时前
《算法竞赛从入门到国奖》算法基础:入门篇-离散化
c语言·数据结构·c++·算法·visual studio
散峰而望2 小时前
OJ 题目的做题模式和相关报错情况
java·c语言·数据结构·c++·vscode·算法·visual studio code
zc.ovo2 小时前
线段树优化建图
数据结构·c++·算法·图论
WaWaJie_Ngen2 小时前
C++实现一笔画游戏
c++·算法·游戏·游戏程序·课程设计
程序员-King.2 小时前
day140—前后指针—删除排序链表中的重复元素Ⅱ（LeetCode-82）
数据结构·算法·leetcode·链表
小尧嵌入式2 小时前
【Linux开发一】类间相互使用|继承类和构造写法|虚函数实现多态|五子棋游戏|整数相除混合小数|括号使用|最长问题
开发语言·c++·算法·游戏
热门推荐
01GitHub 镜像站点022025 Telegram 最新免费社工库机器人（LetsTG可[特殊字符]）搭建指南（含 Python 脚本）03OpenCode 入门教程：介绍 · 安装 · 配置第三方 API (如 Claude)04Linux下V2Ray安装配置指南05UV安装并设置国内源06Claude Code Skills 实用使用手册07AI 规范驱动开发“三剑客”深度对比：Spec-Kit、Kiro 与 OpenSpec 实战指南08Labelme从安装到标注：零基础完整指南09安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）10BongoCat - 跨平台键盘猫动画工具