机器学习笔记

一、监督学习

1、监督学习定义

使用有标签的数据集（给定输入X的正确标签Y）来训练模型。算法最终学会在没有输出标签的情况下仅凭输入就能给出相当准确的预测。

2、应用实例

垃圾邮件过滤 (Spam filtering)：输入是邮件内容，输出是判断这封邮件是否为垃圾邮件（通常用0/1表示）。
语音识别 (Speech recognition)：输入是音频片段，输出是对应的文字记录。
机器翻译 (Machine translation)：输入是一种语言的文本（eg：英语），输出是另一种语言的文本（eg：中文）。
在线广告 (Online advertising)：输入是广告信息和用户信息，输出是用户是否会点击这个广告（0/1）。
自动驾驶 (Self-driving car)：输入是汽车的图像、雷达信息等，输出是路面上其他车辆的位置。
视觉检测 (Visual inspection)：输入是产品的图片（比如手机），输出是判断产品是否存在缺陷（0/1）。

3、监督学习的两种类型

3.1 回归（Regression）

回归问题：预测一个连续的数值。eg：房价预测、气温预测......

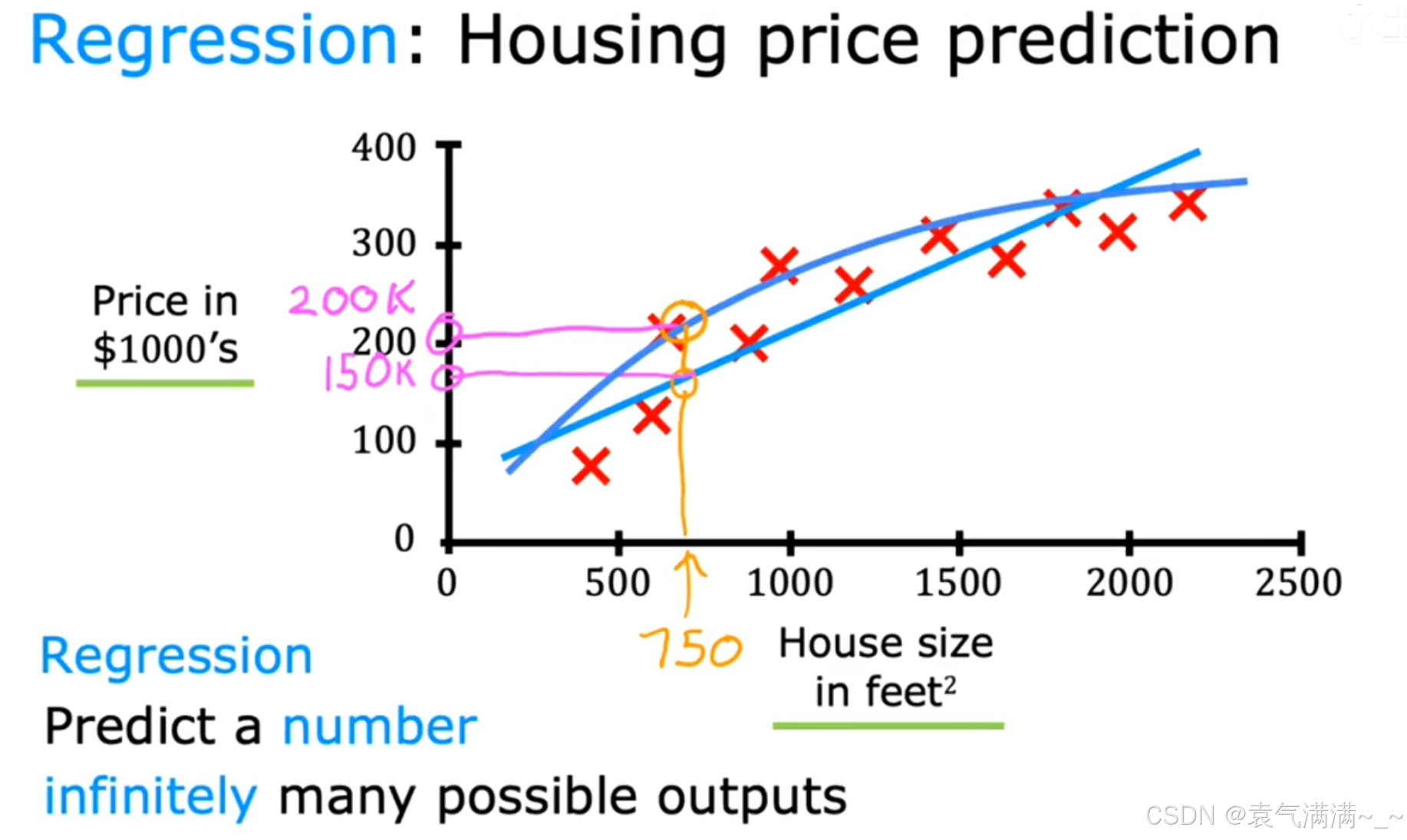
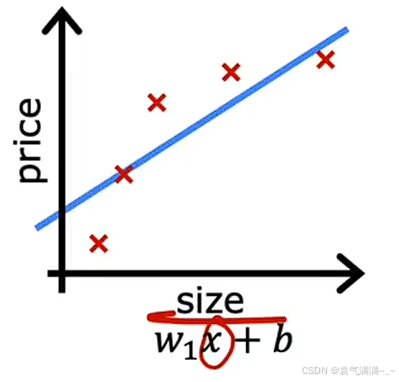
模型（图中的直线或曲线）会尝试去拟合这些数据点，当我们有一个新的输入（比如房屋面积为750平方英尺），模型给出一个预测的价格（比如150k美元）。这就是一个典型的回归问题，其目标是预测一个数字。

3.2 分类（Classification）

分类问题：预测的输出是一个离散的、有限的类别。eg：是否是垃圾邮件、肿瘤是良/恶性......

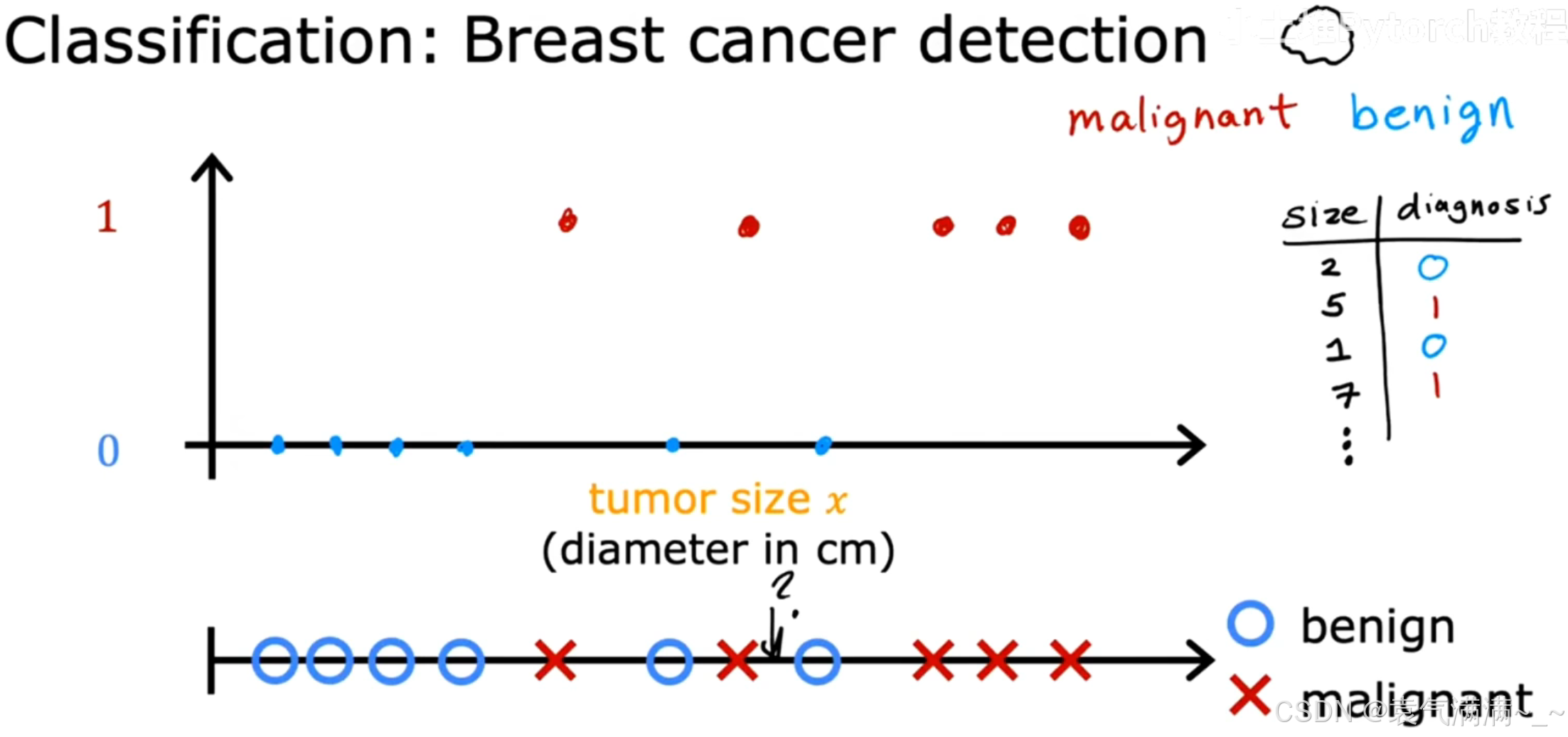
如图所示，我们根据肿瘤的大小（Tumor size）来判断它是良性的（benign）还是恶性的（malignant）。这里的输出只有两个明确的类别（良性/恶性），我们可以用0和1来代表。这就是一个典型的回归问题，其目标是预测一个类别。

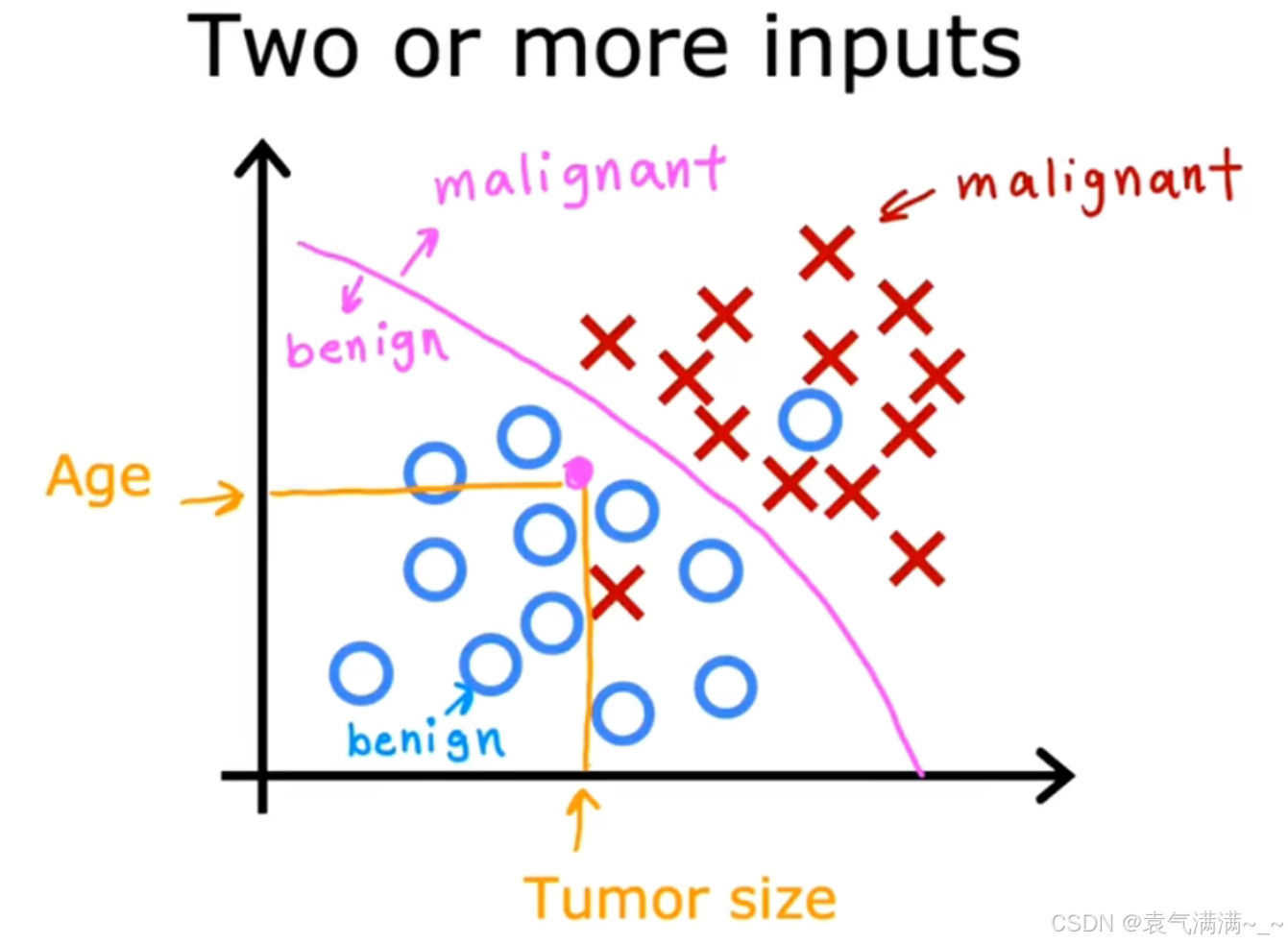
当有多个特征输入时，分类模型会尝试找到一个决策边界，来区分不同的类别。

二、无监督学习

1、无监督学习定义

使用无标签的数据集来训练模型。简单来说，无监督学习的数据只有输入X，没有输出标签Y。

2、类型

2.1 聚类（Clustering）

应用示例：

谷歌新闻：算法自动分析文章内容，将讲述同一个故事的文章聚集到一起。
基因芯片：根据基因表达的相似性将不同的个体进行分组。
客户细分：根据用户的学习行为、兴趣偏好等，将他们分为不同群体，从而提供更加个性化的服务。

2.2 降维 (Dimensionality reduction)

在保留数据最重要特征的前提下，减少数据的变量个数（维度）。

2.3 异常检测 (Anomaly detection)

从数据中识别出那些与正常数据模式显著不同的"异常点"或"离群点"。

三、线性回归模型

1、回归模型 (Regression model)

预测的是一个连续的数值（Numbers），理论上有无限多种可能的输出。

2、模型的专业术语

x: 输入变量 (input variable)，也常被称为特征 (feature)。eg：房屋的面积。
y: 输出变量 (output variable)，也常被称为目标 (target)。eg：房屋的价格。
m: 训练样本的数量 (number of training examples)。eg：47个训练样本，即m=47。
(x, y): 表示一个单个的训练样本。
(x⁽ⁱ⁾, y⁽ⁱ⁾): 表示第 i 个训练样本。这里的上标 (i) 只是一个索引 (index)，代表第几行数据，它不是数学上的指数或次方。eg：(x⁽¹⁾, y⁽¹⁾) 就代表第一个训练样本，即 (2104, 400)。

3、模型训练和预测的流程

将训练集 (training set)（包含了特征 x 和目标 y）喂给一个学习算法 (learning algorithm)。
学习算法会输出一个函数 f。这个函数 f 就是我们最终得到的模型 (model)，在一些文献中它也被称为假设 (hypothesis)。
当有新的输入 x（例如，一个全新的房屋面积）时，我们就可以用这个模型 f 来进行预测。模型输出的预测值，我们通常用 ŷ (读作 "y-hat") 来表示。

4、单变量线性回归(Univariate linear regression)

f 是预测标签（输出）。
b 是模型的偏差。偏差与直线代数方程式中的 y 轴截距概念相同。在机器学习中，偏差有时称为。偏差是模型的形参，在训练期间计算得出。
w 是特征的权重。权重与线性代数方程式中的斜率的概念相同。权重是模型的形参，在训练期间计算得出。
x 是一个特征，即输入。

通过学习算法，找到最优参数 w 和 b ，使其更好的拟合我们的训练数据。

四、代价函数cost function

：计算单个样本的预测值和真实值之间的误差。
(...)²：对误差取平方。这有两个好处：
- 可以确保误差值为正，避免正负误差相互抵消。
- 可以放大较大误差的惩罚，使得模型更倾向于去拟合那些偏差大的点。
Σ [...]：将所有 m 个训练样本的平方误差求和。
(1 / 2m)：求平均值。除以 m 是为了让代价函数的值不受样本数量的影响。而乘以 1/2 是一个数学上的小技巧，它可以在后续计算（求导）时简化公式，但并不会影响我们找到最优 w 和 b。

目标：找到能使代价函数 J(w, b) 最小的 w 和 b 的值。

五、梯度下降

优化代价函数，找到最小值。

1、流程

初始化：为w和b赋一个初始值（通常为0）
迭代更新：改变w和b的值使J(w,b)减小
收敛：代价函数最终稳定在或接近最小值

2、实现

=：赋值
α：学习率，介于0和1之间，控制更新w和b时所采取的步长
：指明下降的方向
**同时更新 w 和 b ，**按如图所示逐步进行

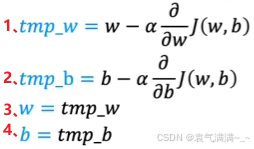
2.1 导数项

导数实质上就是代价函数曲线在当前 w 点的切线斜率。

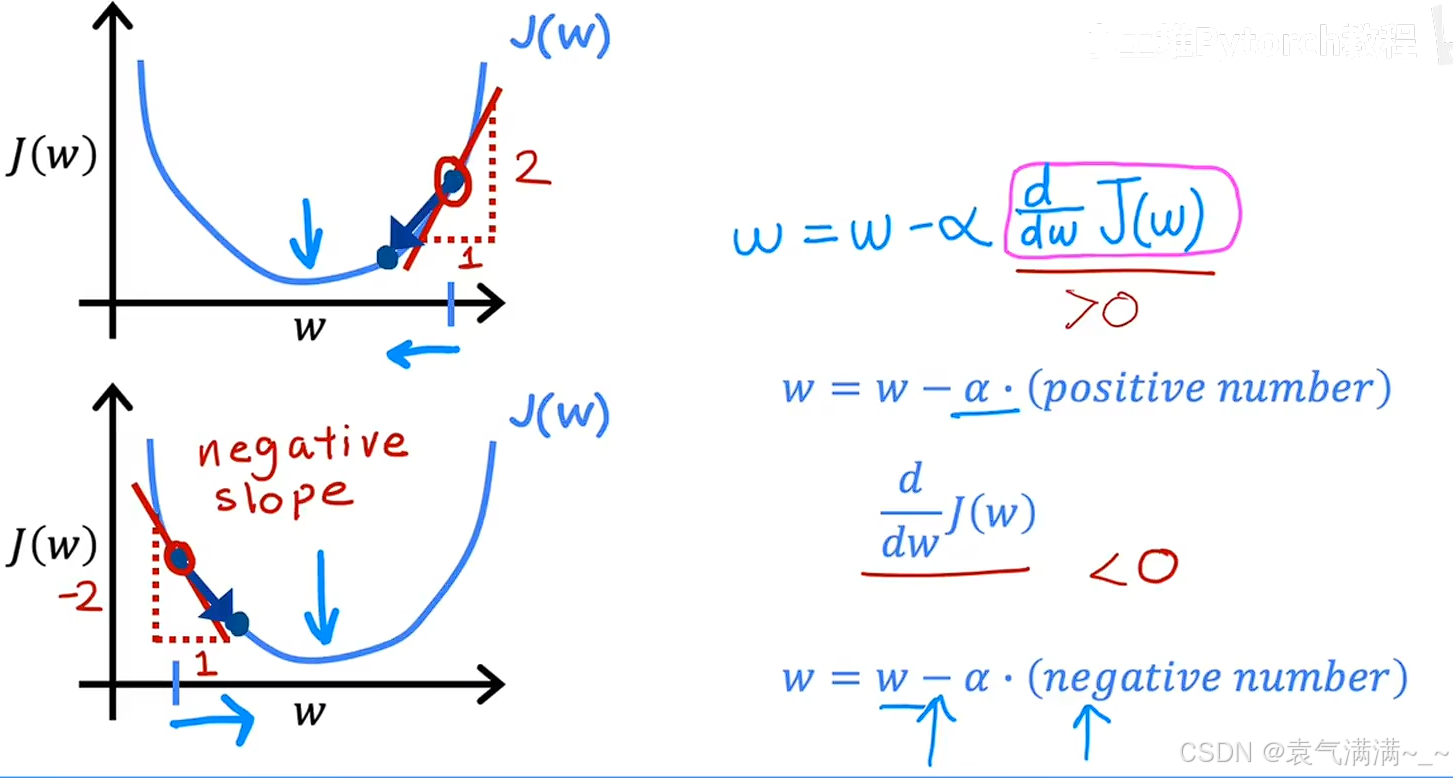
导数 > 0：w位于最低点的右侧，斜率为正， > 0， > 0，w减去正数得到一个比原来更小的值，此时w值向左移动，更靠近最低点
导数 < 0：w位于最低点的左侧，斜率为负， < 0， < 0，w减去负数得到一个比原来更大的值，此时w值向右移动，更靠近最低点

2.2 学习率 α

α 控制每一步更新的步长。

α太小：梯度下降算法需要很多步，收敛速度慢
α太大：可能会略过最小值，甚至可能永远无法到达最小值，梯度下降算法可能无法收敛，甚至可能发散

3、特性

3.1 在局部最小点停止更新

当 w 到达一个局部最低点时，该点的切线斜率（）为0。此时， = 0，w 的值将不再改变，算法自然收敛。

3.2 即使α固定，更新步长也会自动变小

当接近最低点时，曲线会变得越来越平缓，导数的值也自然会越来越小。这就意味着，即使α是一个固定的值，这个整体的更新步长也会自动减小，使梯度下降算法可以在接近最优解时进行更精细的调整，从而平稳地收敛到最低点，而不需要我们手动去减小α。

4、线性回归的梯度下降

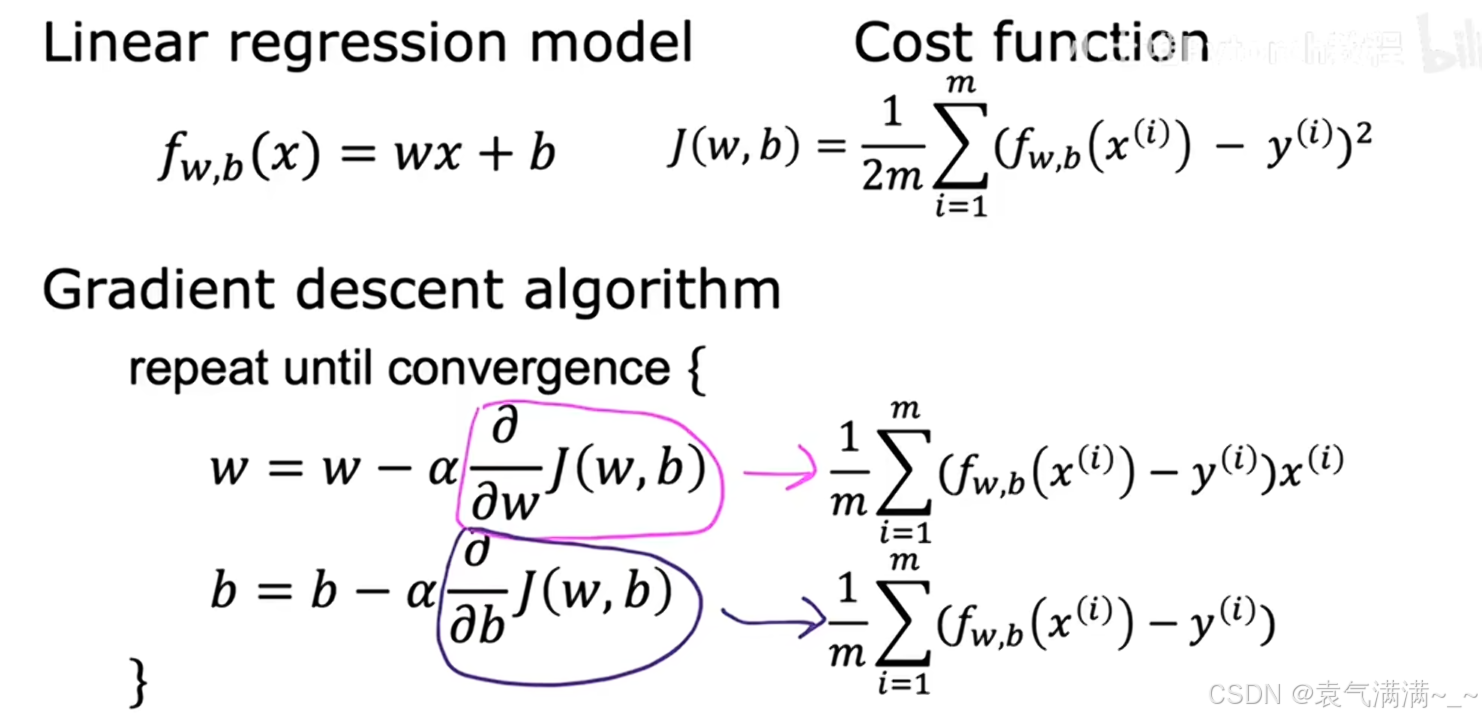
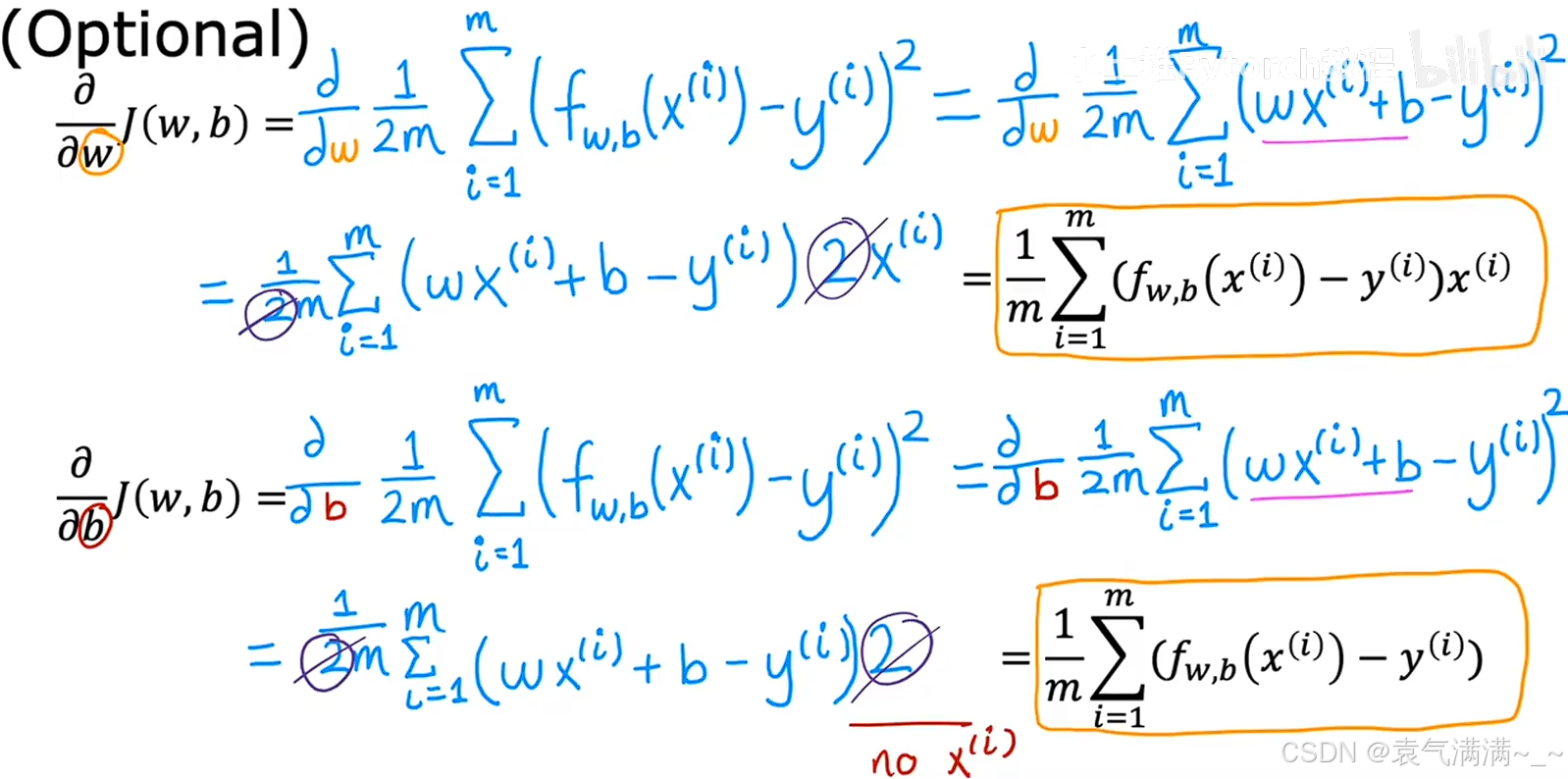
4.1 工作原理

梯度下降可能会陷入局部最小值而不是全局最小值（图1），但使用线性回归的平方误差代价函数时，由于代价函数是一个凸函数，所以不会有多个局部最小值，只有一个最低点，既是全局最小值又是局部最小值（图2）。

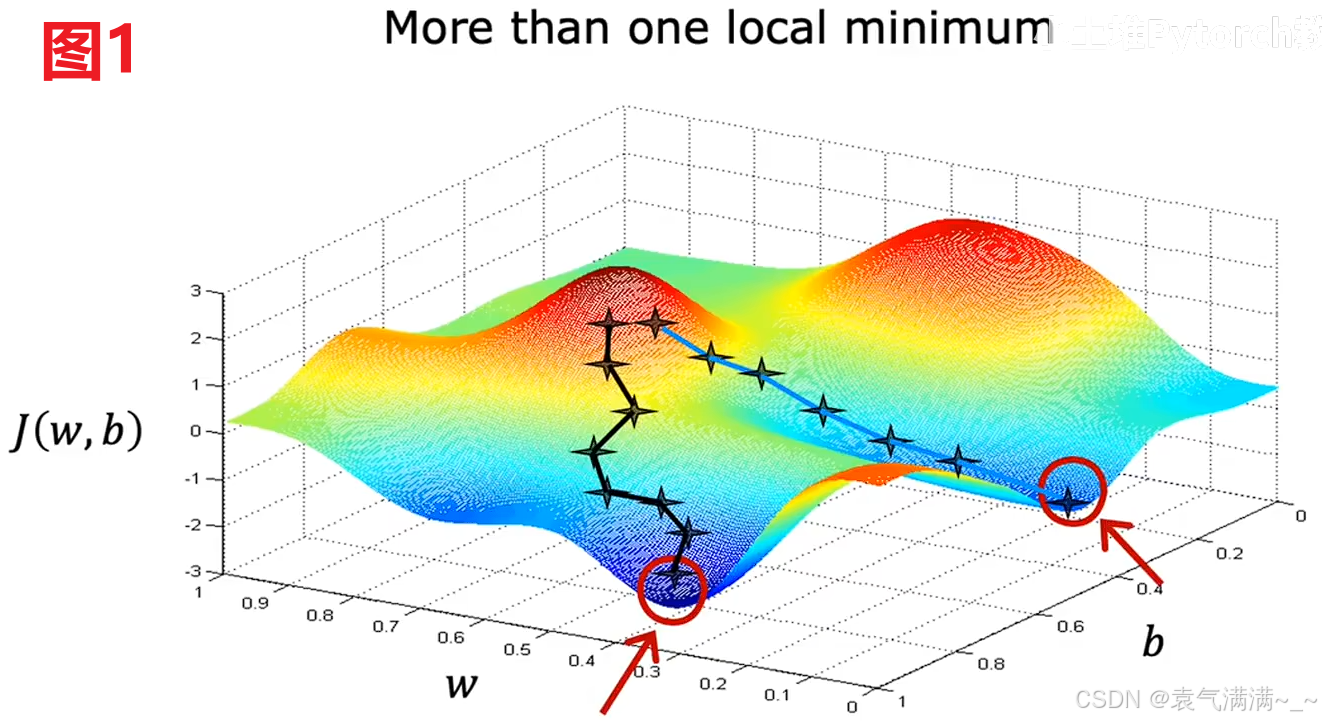
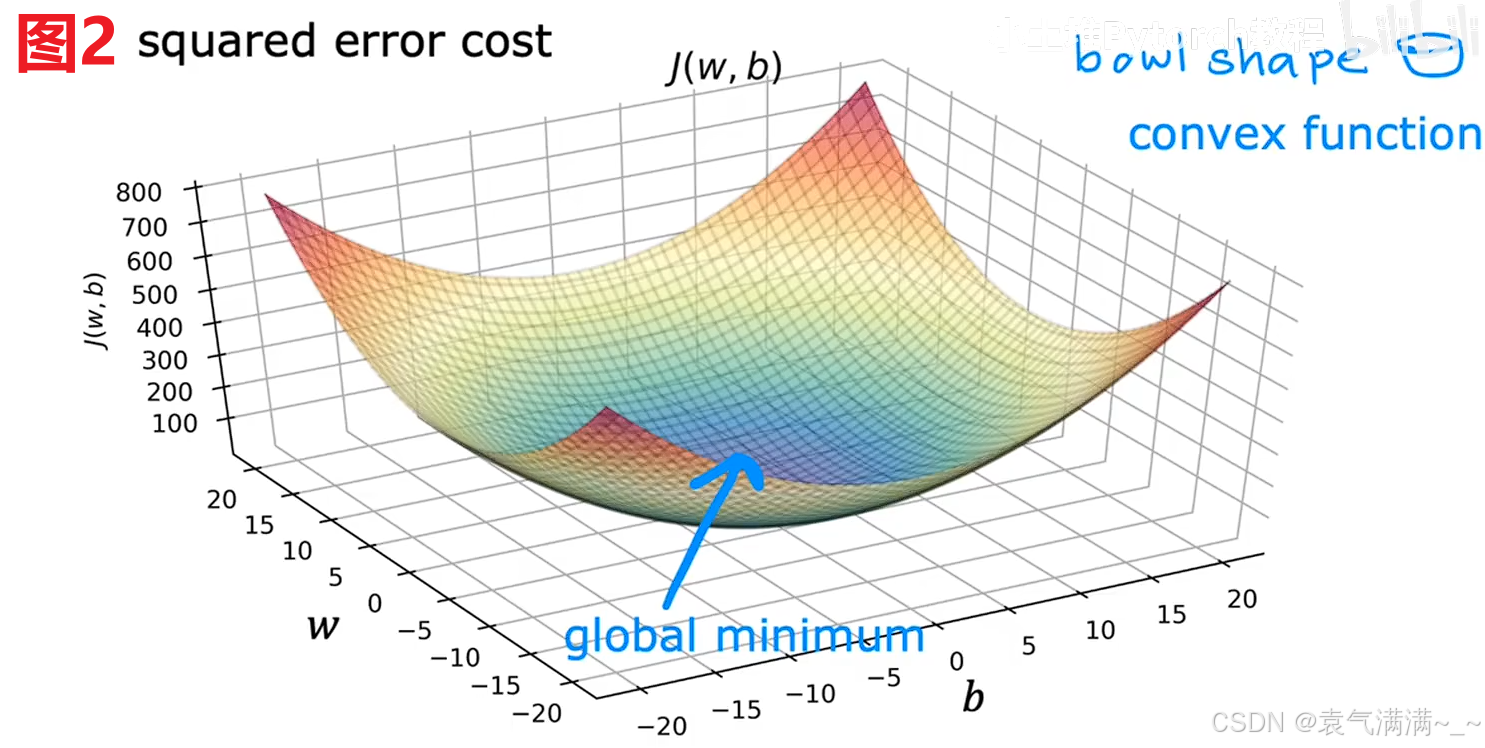
只要我们选择适当的学习率，它总是会收敛到全局最小值。

4.2 批量梯度下降（batch gradient descent）

batch→在梯度下降的每一步，都使用了所有的训练样本 i∈[1,m] 。

六、多元线性回归

1、符号表示

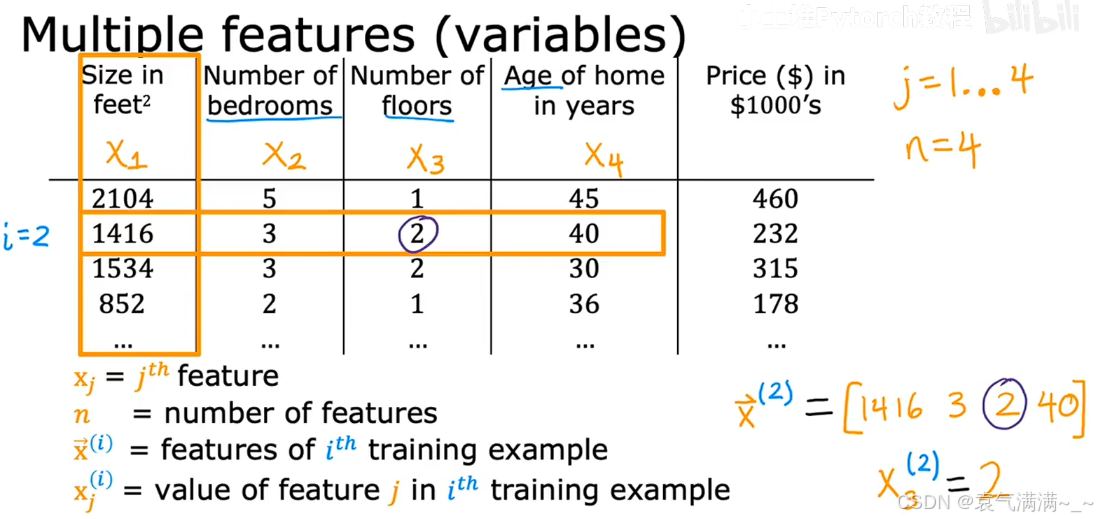
：第 j 个特征。即房屋面积，即房屋的年份。
n：特征总数。图中所示 n=4。
：第 i 个序列样本的所有特征。
：第 i 个序列样本的第 j 个特征。

2、模型表示

2.1 向量化表示

python 复制代码

import numpy as np

w = np.array([1,2.5,-3.3])
b = 4
x = np.array([10,20,30])

f=np.dot(w,x)+b    # 通过向量化既可以简化代码，也可以实现更快的计算。
# 底层原理
# for 循环是串行计算，一步一步执行。
# 向量化的点积操作，可以利用底层硬件实现并行计算，一次性完成所有元素的乘法和加法，当特征数量 n 很大时，向量化的计算速度会比 for 循环快得多。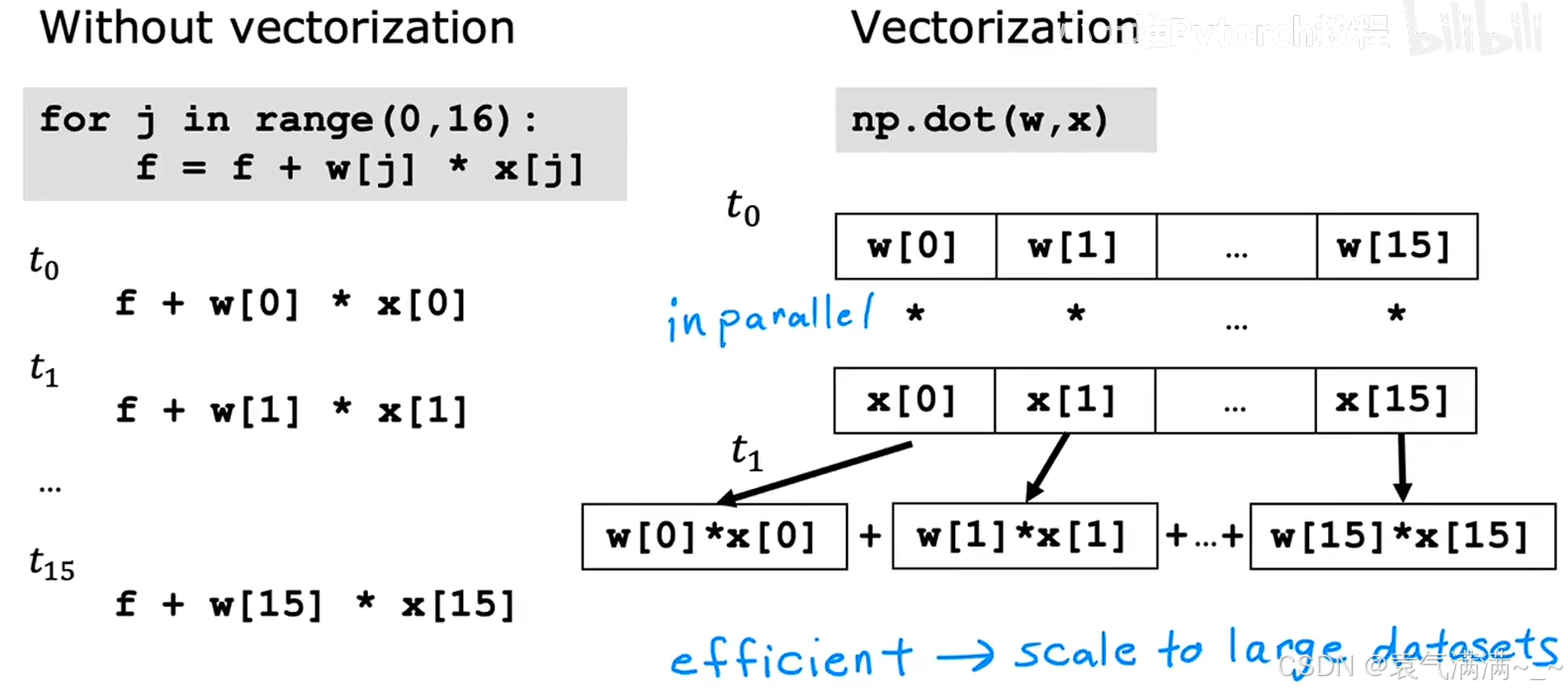

3、梯度下降

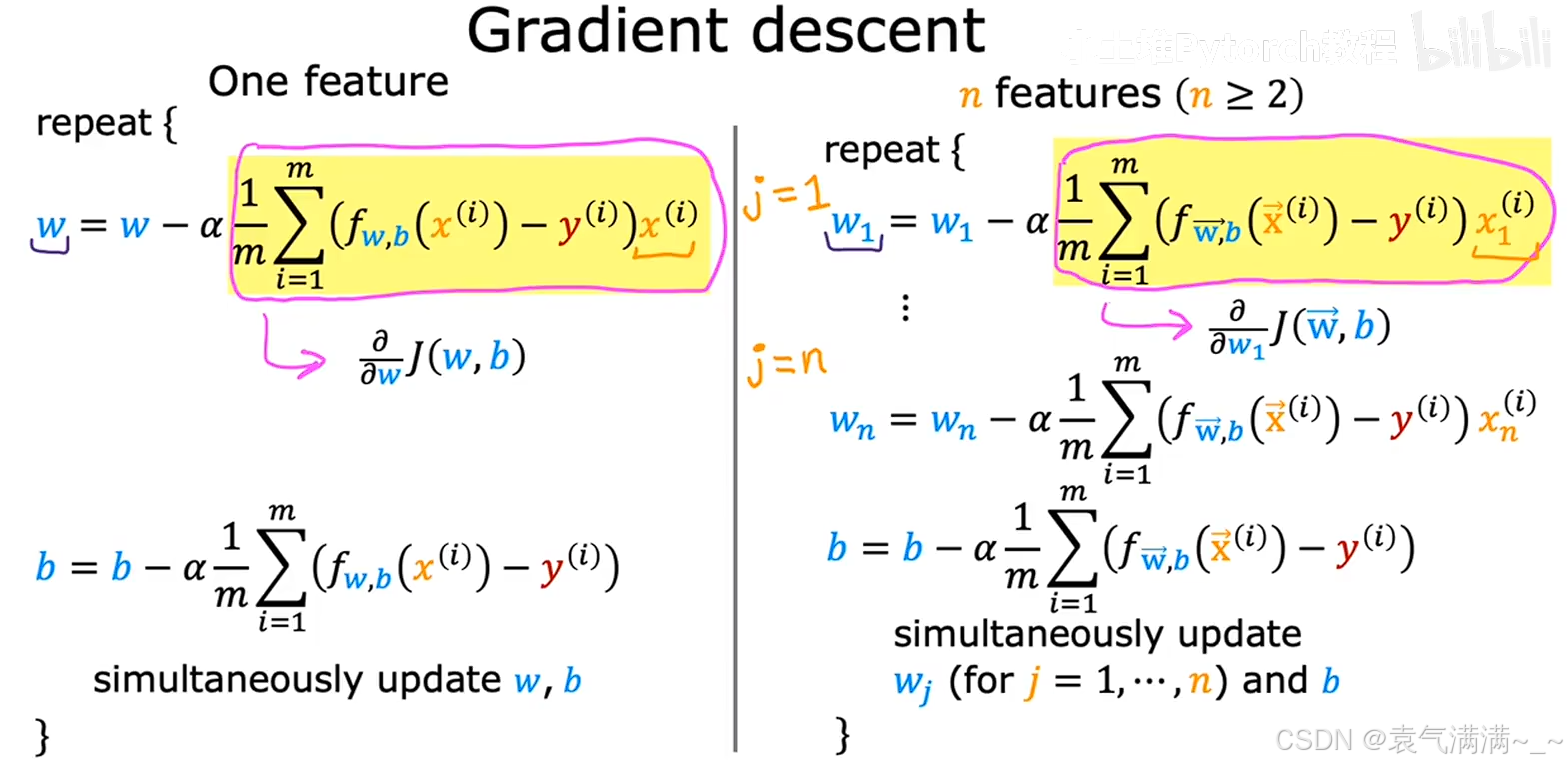
4、正规方程

除了梯度下降，还可以通过正规方程（normal equation）来确定w和b的值。

只适用于线性回归
如果特征数量n很大（>10000），计算速度也会很慢
可通过高级线性代数库一次性求解w和b，无需迭代

七、特征缩放

如图所示，有两个特征：房屋面积 x₁∈[300,2000]、卧室数量 x₂∈[0,5]。这两个特征的取值范围相差巨大，导致范围较小的特征 （）最终可能会对应一个数值较大的参数 ，范围较大的特征（）最终可能会对应一个数值较小的参数。此时，散点图和等高线图呈现效果一般。

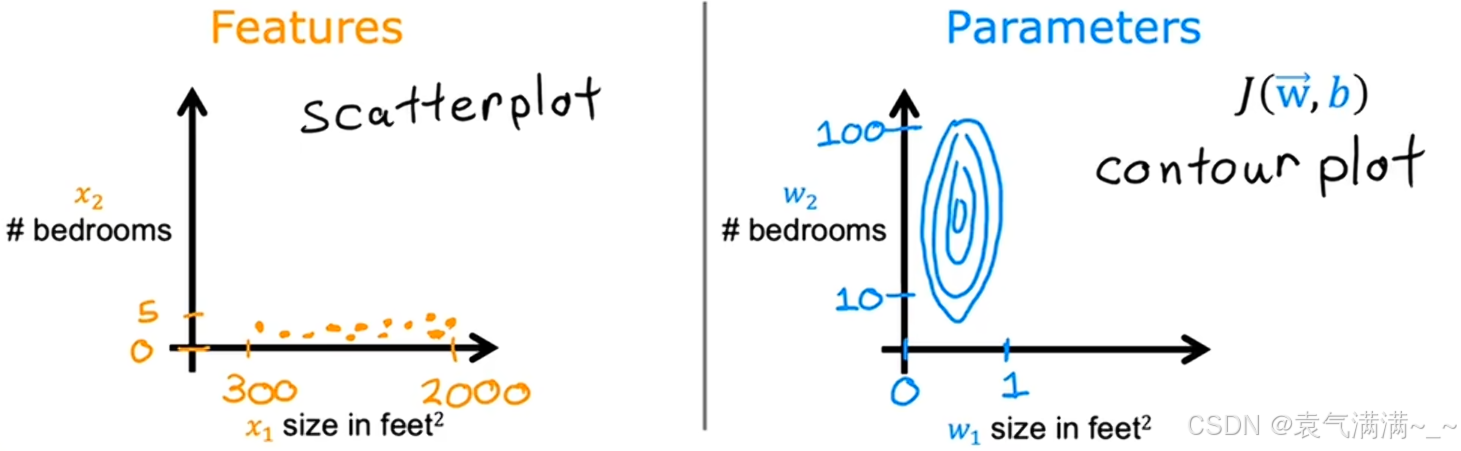
通过特征缩放，将所有特征的取值范围都缩放到一个相似的区间（例如 0 到 1），等高线图也变得更"圆"。

1、方法

1.1 最大值归一化

将每个特征值除以该特征的最大值，得到特征缩放后的区间。

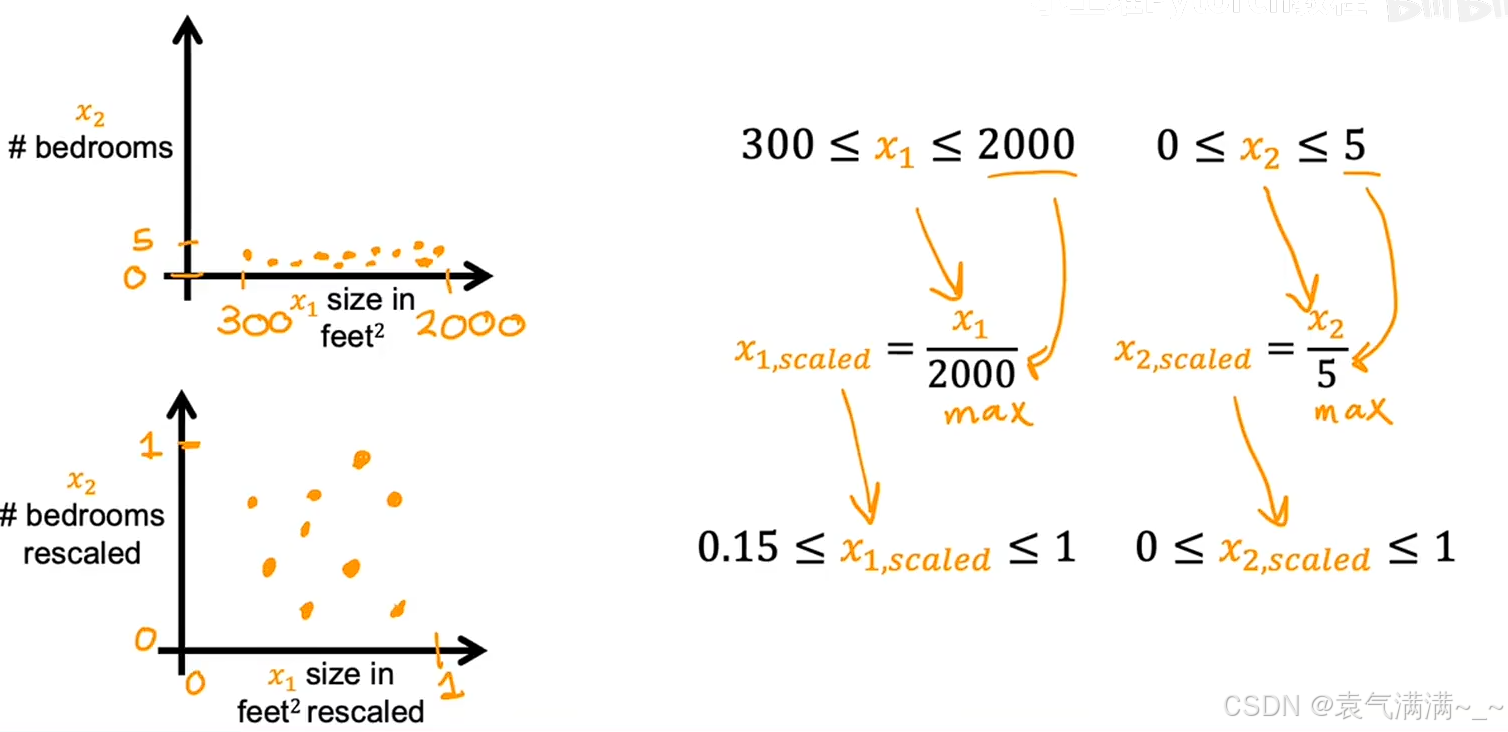
1.2 均值归一化

将每个特征值减去该特征的平均值，再除以最大值减去最小值的结果。

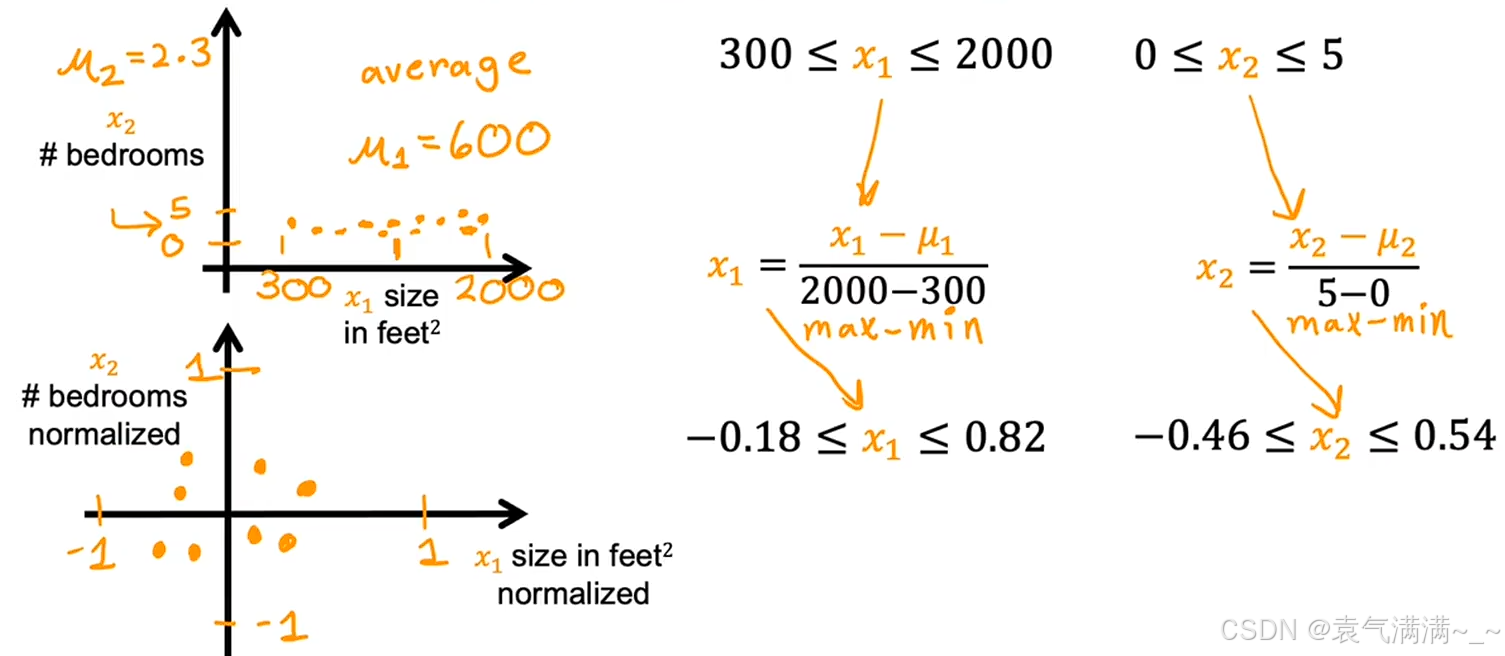
1.3 Z-score归一化

将每个特征值减去该特征的平均值，再除以标准差。

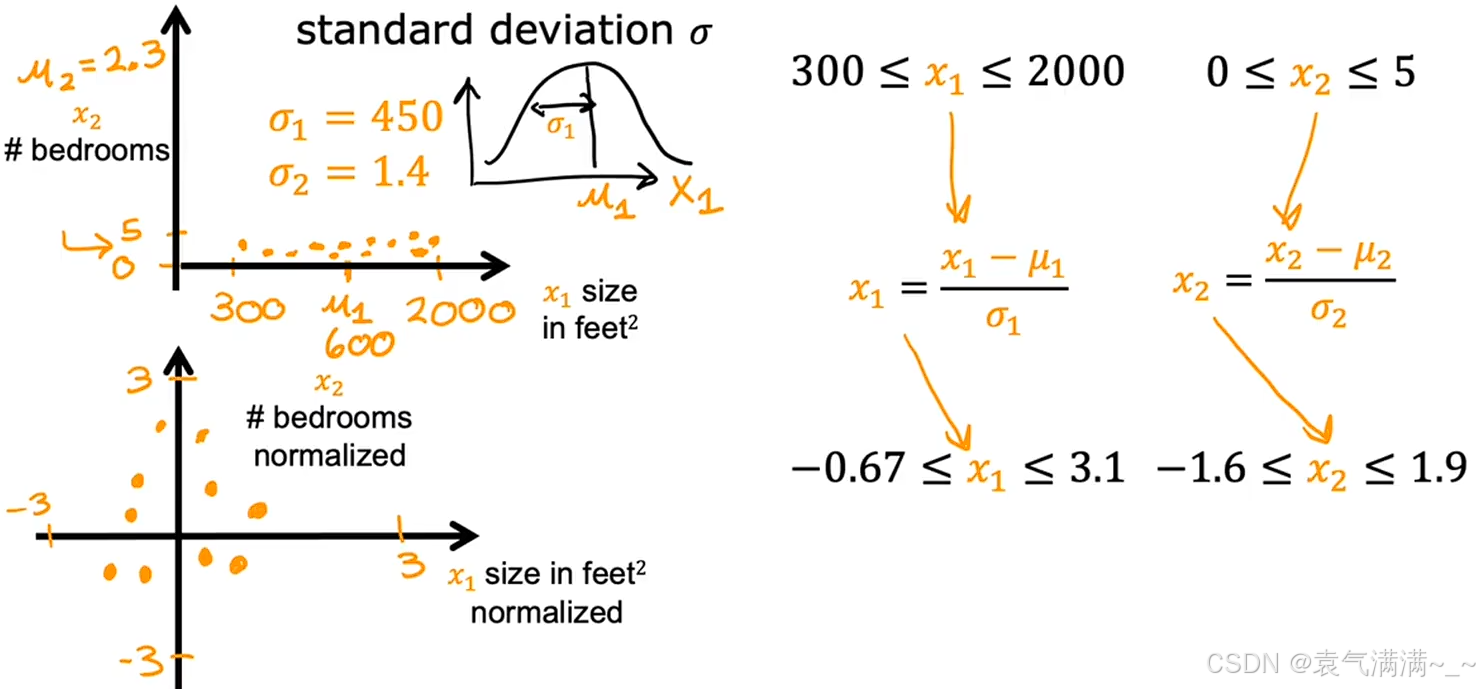
2、经验法则

尽量将每个特征 xⱼ 的范围控制在 -1 到 1 附近。

像 0 ≤ xⱼ ≤ 3，-2 ≤ xⱼ ≤ 0.5 是可以接受的
像 -3 ≤ xⱼ ≤ 3， -0.3 ≤ xⱼ ≤ 0.3也问题不大
像-100 ≤ xⱼ ≤ 100， -0.001 ≤ xⱼ ≤ 0.001需要重新特征缩放

八、逻辑回归

1、逻辑回归与分类问题

分类问题的目标是预测一个离散的类别。

逻辑回归的核心思想是，将线性回归的输出结果，通过Sigmoid函数（Logistic函数） ，压缩到 0 和 1 之间。

2、Sigmoid/Logistic 函数

3、模型表示

逻辑回归模型将线性部分的结果，作为 Sigmoid 函数的输入z。

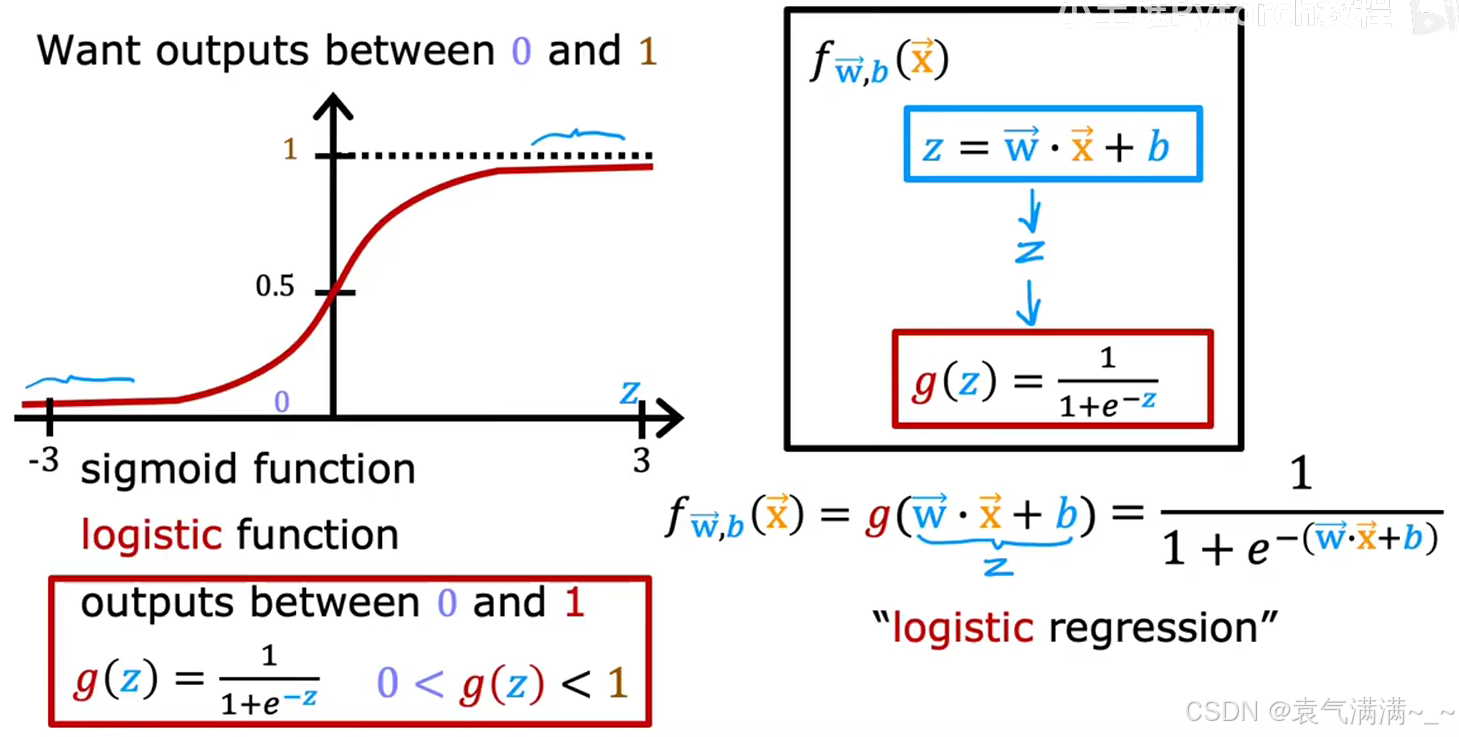
逻辑回归模型的输出值有一个非常好的概率解释：它代表了在给定 x 的条件下，预测类别为 1 的概率 。即：

eg：如果模型对一个肿瘤样本输出 0.7，这意味着模型认为该肿瘤有70%的概率是恶性（y=1）的。

4、决策边界

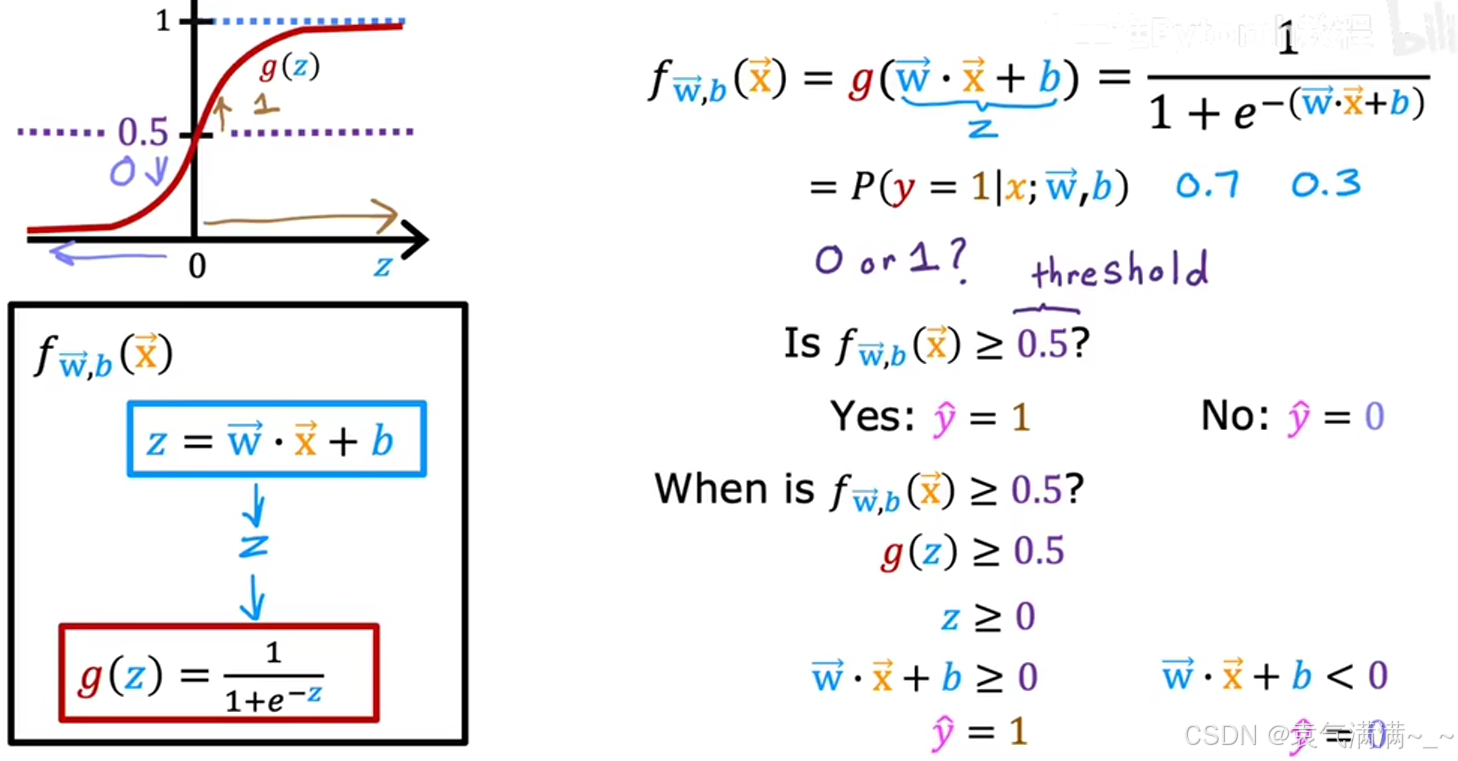
如图所示，以0.5为阈值，判断是否大于0.5。

若，则预测，
若，则预测。

由于 Sigmoid 函数 g(z) 在 z=0 时取值为 0.5，所以上述决策规则等价于：

若，则预测，
若，则预测。

此时，由所定义的线（或面）就是决策边界。它将特征空间一分为二，一边是预测为 1 的区域，另一边是预测为 0 的区域。

4.1 线性决策边界

当 z 是特征的线性组合时（eg：z = x₁ + x₂ - 3 = 0），决策边界就是线性的（eg：x₁ + x₂ = 3）。

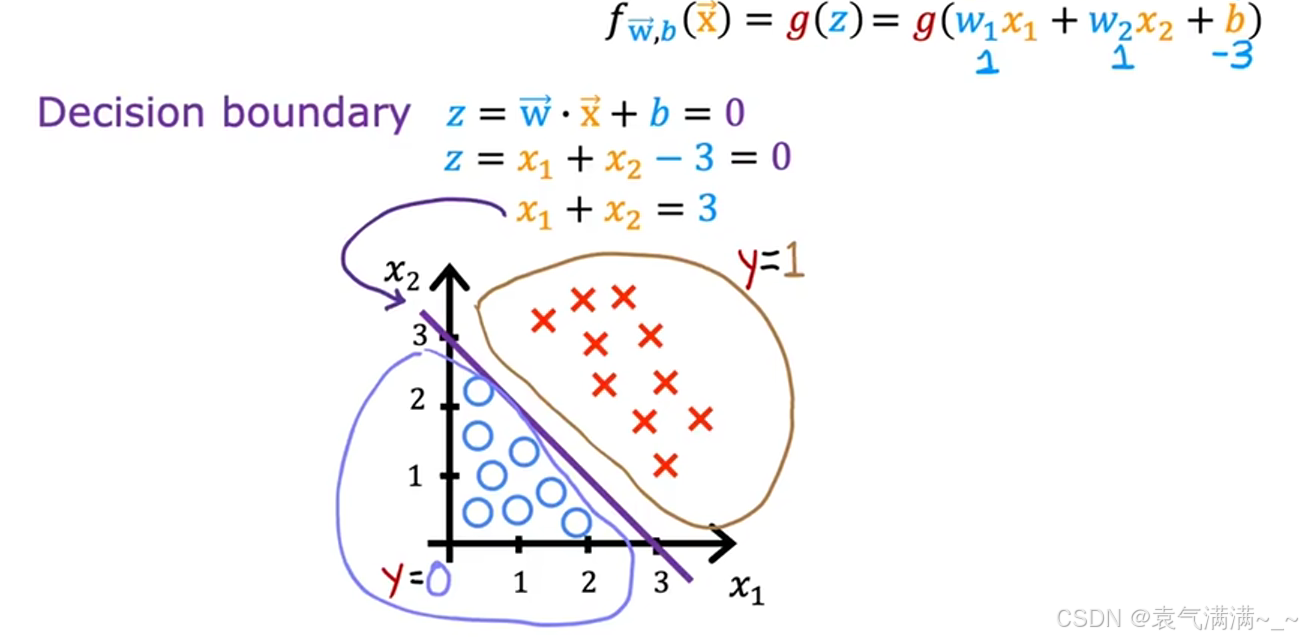
4.2 非线性决策边界

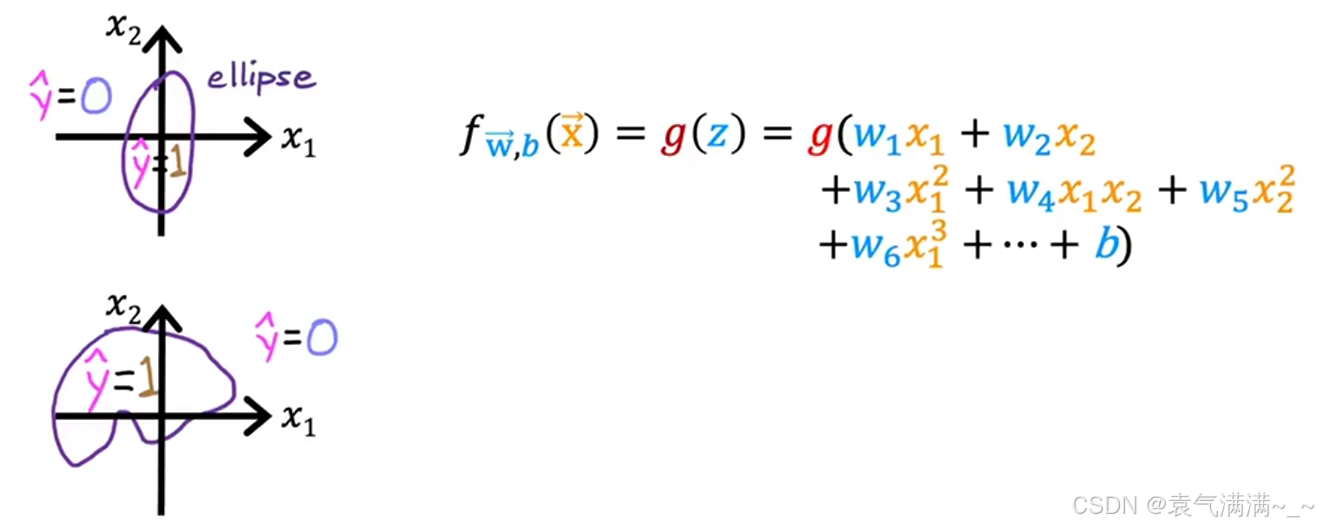
5、代价函数

为了构建逻辑回归的代价函数，首先为单个训练样本定义一个损失函数（Loss Function） ，即。

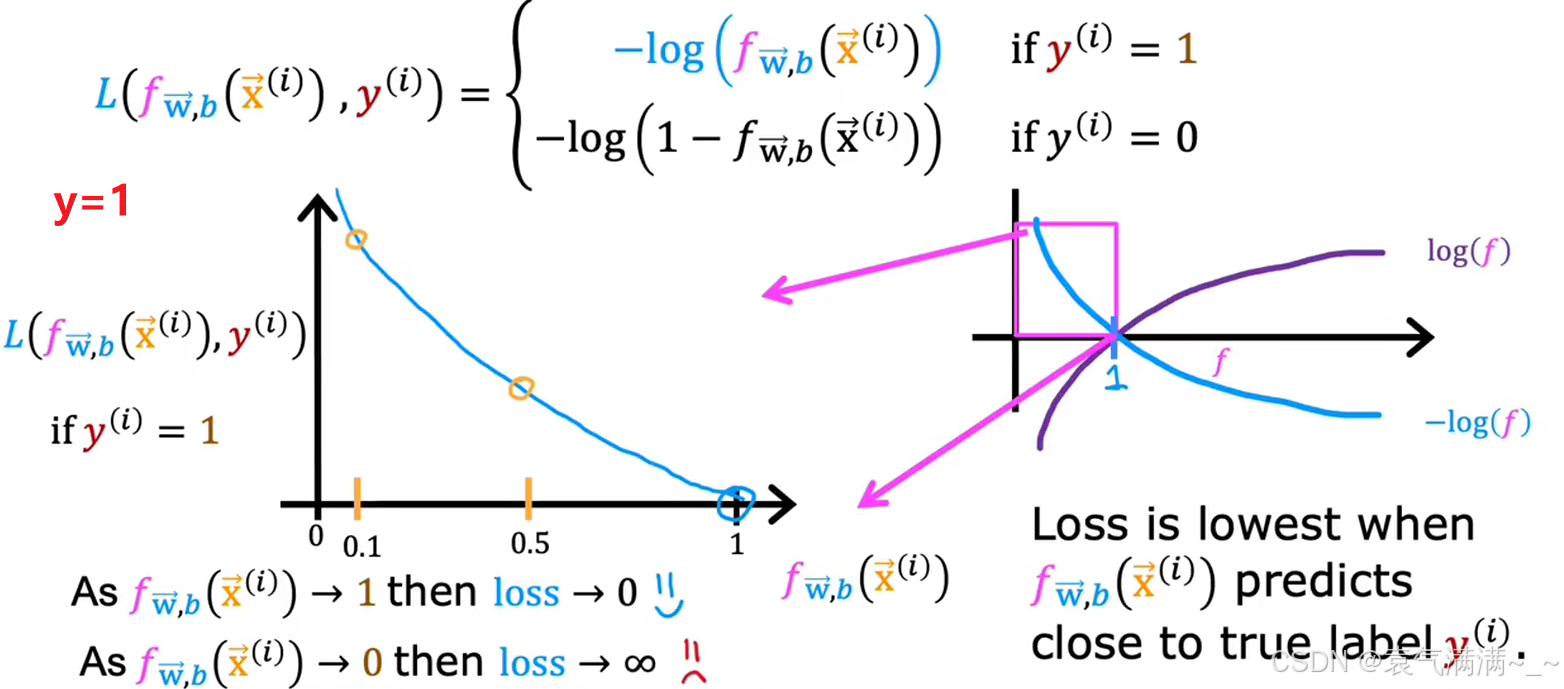
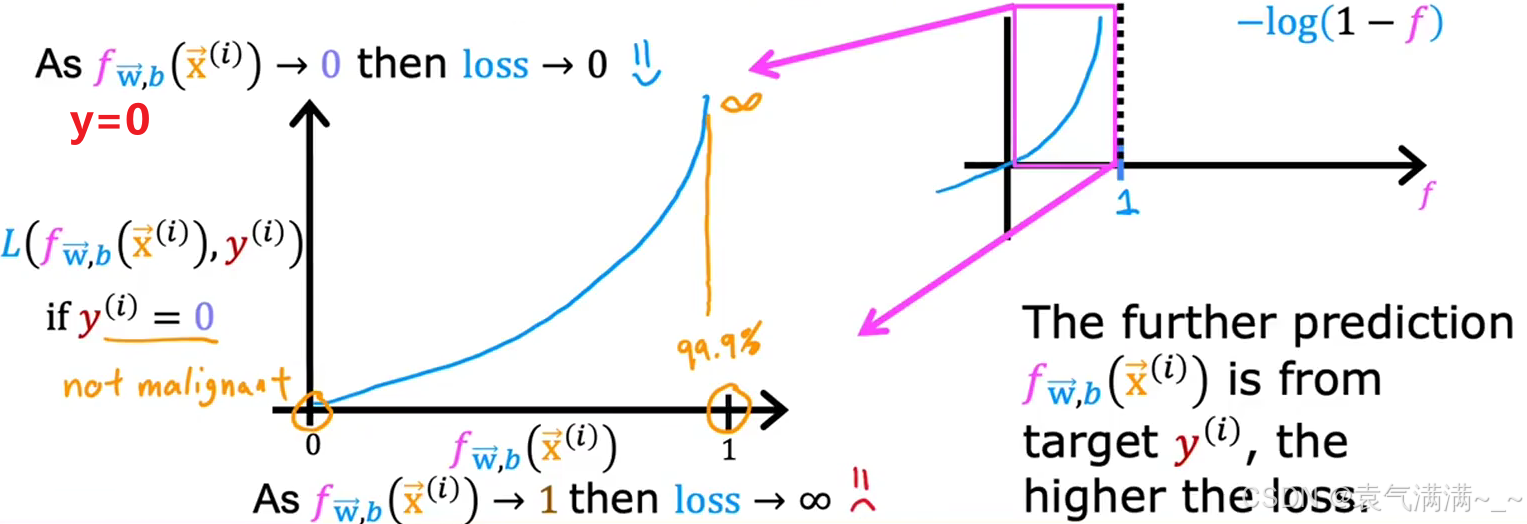
损失函数衡量的是在单个训练样本上的表现，通过将所有训练样本的损失相加，就可以得到代价函数。

简化后的损失函数

简化后的代价函数

6、梯度下降

九、过拟合与欠拟合

|----------------------------------------------------------------------------|----------------------------------------------------------------------------|-----------------------------------------------------------------------------------------------------------------|
| | | |
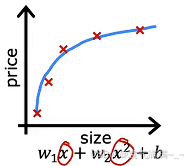
| 欠拟合 | 适度拟合 | 过拟合 |
| 模型不能很好地捕捉数据的整体趋势，对训练集的拟合程度差。这种情况也被称为模型存在高偏差。 | 反映了数据的一般规律。这可能是一个泛化能力较好的模型。 | 模型为迁就每个训练数据点，导致曲线变得异常扭曲。虽然它在训练集上表现得"极其完美"，但它学习到的可能不是数据的普遍规律，而是训练集特有的噪声。这种模型对新数据的预测能力可能会很差，也被称为模型存在高方差。 |
| 解决办法： 1. 增加模型复杂度 2. 减少正则化 3. 特征工程 4. 增加训练时间 | ------ | 解决办法： 1. 收集更多的训练数据 2. 特征选择 3. 正则化 |

十、正则化

核心思想：在损失函数中直接添加一个基于模型权重参数的惩罚项。

1、带正则化的代价函数

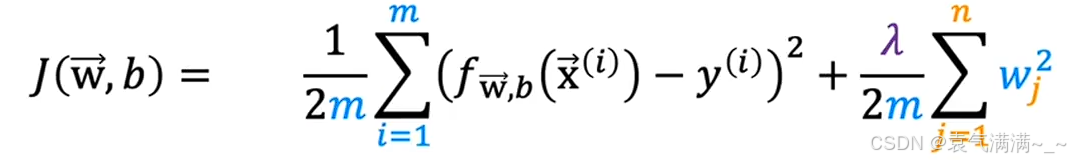
λ是正则化参数
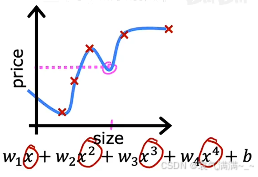
- λ越大，对大参数的惩罚就越重，模型就会让 wⱼ 越小，模型就会变得更简单，更容易欠拟合
- λ=0，正则化项不起作用，模型更容易过拟合

2、正则化线性回归与正则化逻辑回归

|------|--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|
| | 正则化线性回归 | 正则化逻辑回归 |
| 代价函数 | | |
| 梯度下降 | | |

十一、相关练习

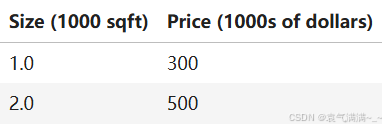
1、通过这两个点拟合一个线性回归模型，并预测其他房子的价格------比如一栋 1200 平方英尺的房子。

python 复制代码

# practice1.ipynb
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('./deeplearning.mplstyle')

# x_train is the input variable (size in 1000 square feet)
# y_train is the target (price in 1000s of dollars)
x_train = np.array([1.0, 2.0])
y_train = np.array([300.0, 500.0])
print(f"x_train = {x_train}")
print(f"y_train = {y_train}")

# 查看训练样本的数量m
print(f"x_train.shape: {x_train.shape}")
m = x_train.shape[0]    # m = len(x_train)
print(f"Number of training examples is: {m}")    # m = 2

# 查看训练实例(x^(i), y^(i))
i = 0
x_i = x_train[i]
y_i = y_train[i]
print(f"(x^({i}), y^({i})) = ({x_i}, {y_i})")    # (x^(0), y^(0)) = (1.0, 300.0)

# 绘制数据
plt.scatter(x_train, y_train, marker='x', c='r')
# Set the title
plt.title("Housing Prices")
# Set the y-axis label
plt.ylabel('Price (in 1000s of dollars)')
# Set the x-axis label
plt.xlabel('Size (1000 sqft)')
plt.show()

w = 200
b = 100
print(f"w: {w}")
print(f"b: {b}")

# 定义模型函数 f = wx + b
def compute_model_output(x, w, b):
    """
    Computes the prediction of a linear model
    Args:
      x (ndarray (m,)): Data, m examples 
      w,b (scalar)    : model parameters  
    Returns
      y (ndarray (m,)): target values
    """
    m = x.shape[0]
    f_wb = np.zeros(m)
    for i in range(m):
        f_wb[i] = w * x[i] + b
        
    return f_wb

# 调用模型函数
tmp_f_wb = compute_model_output(x_train, w, b,)

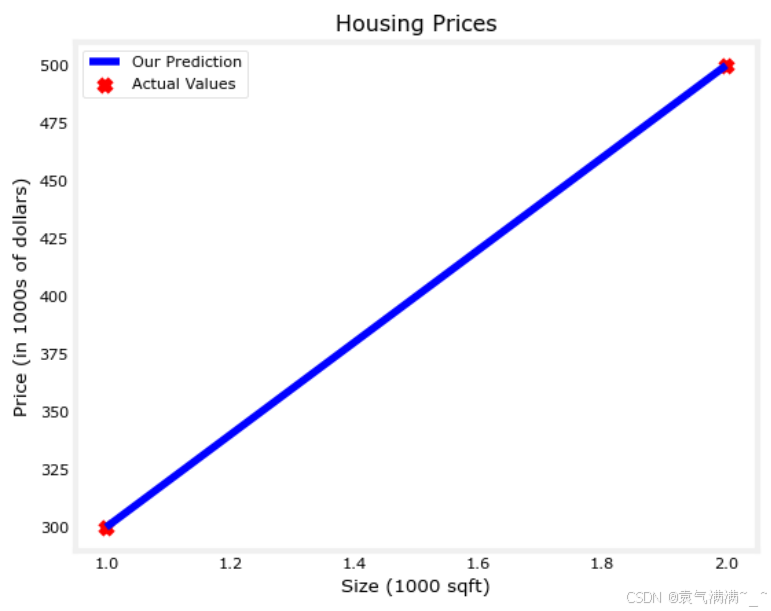
# 绘制模型预测
plt.plot(x_train, tmp_f_wb, c='b',label='Our Prediction')
plt.scatter(x_train, y_train, marker='x', c='r',label='Actual Values')
plt.title("Housing Prices")
plt.ylabel('Price (in 1000s of dollars)')
plt.xlabel('Size (1000 sqft)')
plt.legend()
plt.show()

# 预测
w = 200                         
b = 100    
x_i = 1.2
cost_1200sqft = w * x_i + b    
print(f"${cost_1200sqft:.0f} thousand dollars")    # $340 thousand dollars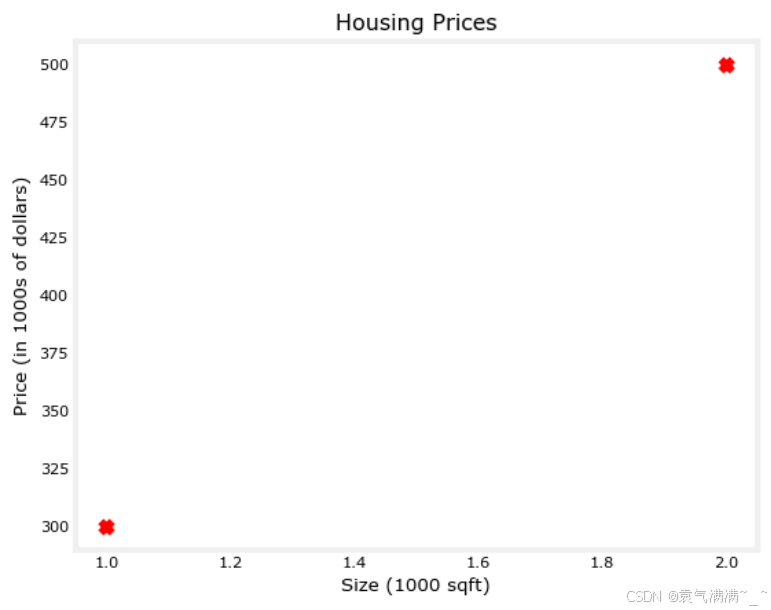

2、代价函数可视化

python 复制代码

import numpy as np
%matplotlib widget
import matplotlib.pyplot as plt
from lab_utils_uni import plt_intuition, plt_stationary, plt_update_onclick, soup_bowl
plt.style.use('./deeplearning.mplstyle')

x_train = np.array([1.0, 2.0])
y_train = np.array([300.0, 500.0])

# 定义代价函数
def compute_cost(x, y, w, b): 
    """
    Computes the cost function for linear regression.
    
    Args:
      x (ndarray (m,)): Data, m examples 
      y (ndarray (m,)): target values
      w,b (scalar)    : model parameters  
    
    Returns
        total_cost (float): The cost of using w,b as the parameters for linear regression
               to fit the data points in x and y
    """
    # number of training examples
    m = x.shape[0] 
    
    cost_sum = 0 
    for i in range(m): 
        f_wb = w * x[i] + b   
        cost = (f_wb - y[i]) ** 2  
        cost_sum = cost_sum + cost  
    total_cost = (1 / (2 * m)) * cost_sum  

    return total_cost

# 找到最适合的w
plt_intuition(x_train,y_train)

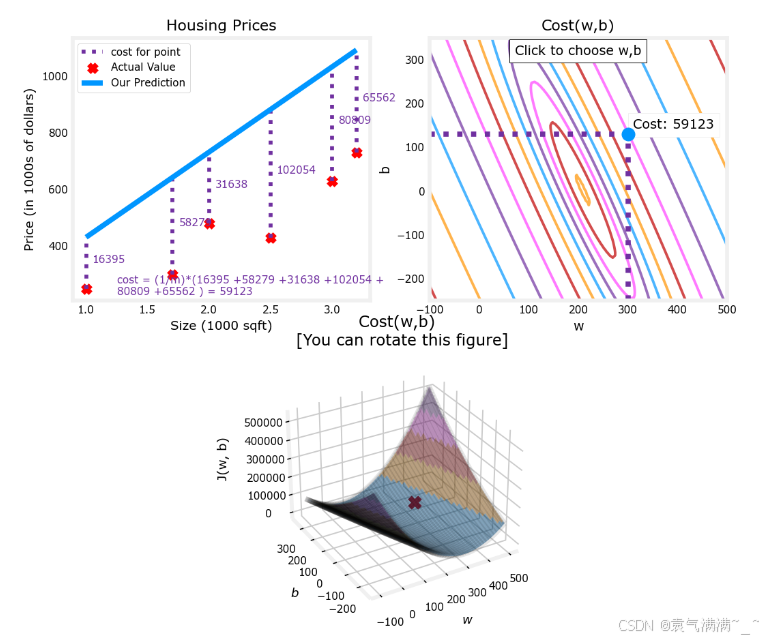
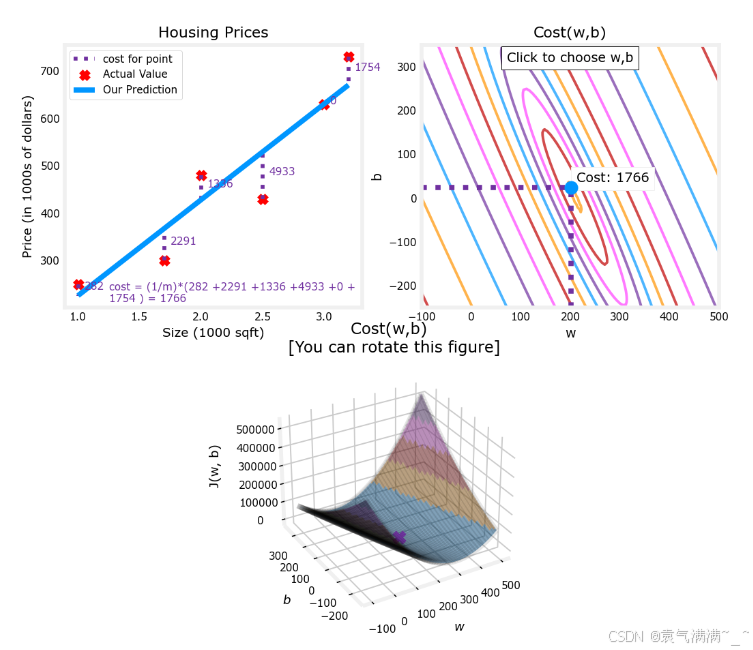
# 绘制更大的数据集
# 在等高线图中，可以点击一个点选择 w 和 b 获得最低成本
x_train = np.array([1.0, 1.7, 2.0, 2.5, 3.0, 3.2])
y_train = np.array([250, 300, 480,  430,   630, 730,])
plt.close('all') 
fig, ax, dyn_items = plt_stationary(x_train, y_train)
updater = plt_update_onclick(fig, ax, x_train, y_train, dyn_items)

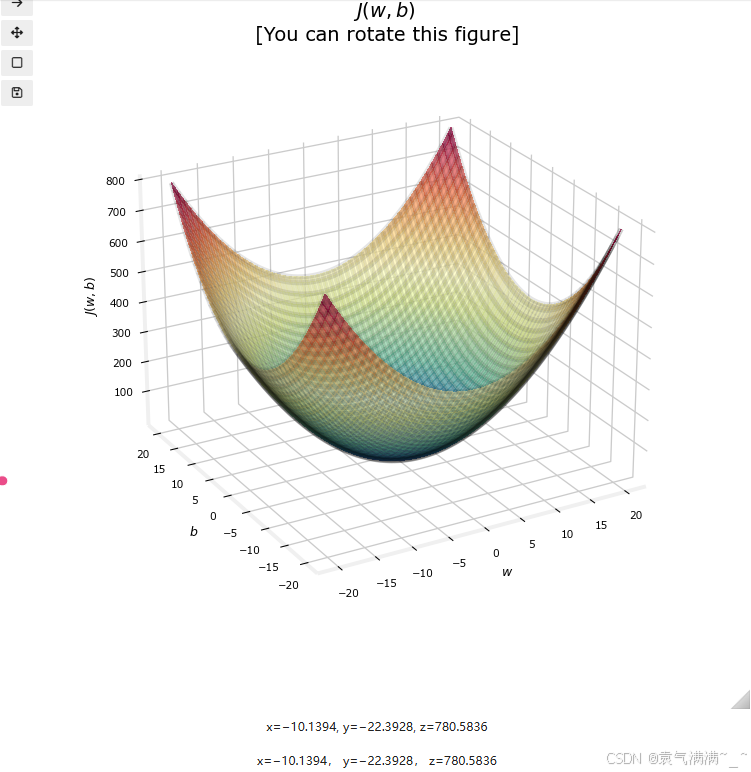
# 凸成本曲面
soup_bowl()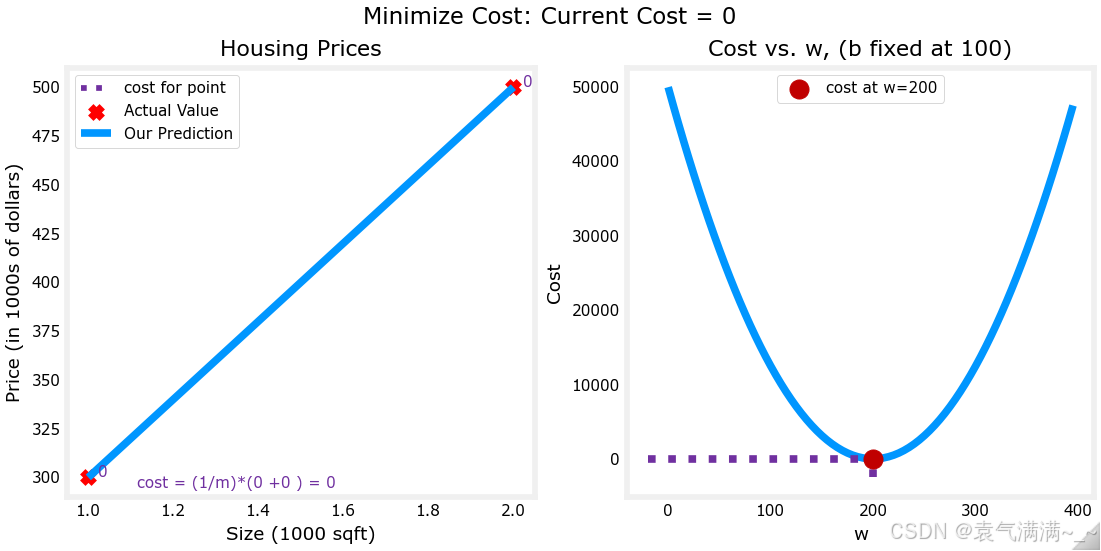

3、梯度下降

python 复制代码

import math, copy
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('./deeplearning.mplstyle')
from lab_utils_uni import plt_house_x, plt_contour_wgrad, plt_divergence, plt_gradients

x_train = np.array([1.0, 2.0])   #features
y_train = np.array([300.0, 500.0])   #target value

def compute_cost(x, y, w, b):
   
    m = x.shape[0] 
    cost = 0
    
    for i in range(m):
        f_wb = w * x[i] + b
        cost = cost + (f_wb - y[i])**2
    total_cost = 1 / (2 * m) * cost

    return total_cost

# 计算偏导数并返回
def compute_gradient(x, y, w, b): 
    """
    Computes the gradient for linear regression 
    Args:
      x (ndarray (m,)): Data, m examples 
      y (ndarray (m,)): target values
      w,b (scalar)    : model parameters  
    Returns
      dj_dw (scalar): The gradient of the cost w.r.t. the parameters w
      dj_db (scalar): The gradient of the cost w.r.t. the parameter b     
     """
    
    # Number of training examples
    m = x.shape[0]    
    dj_dw = 0
    dj_db = 0
    
    for i in range(m):  
        f_wb = w * x[i] + b 
        dj_dw_i = (f_wb - y[i]) * x[i] 
        dj_db_i = f_wb - y[i] 
        dj_db += dj_db_i
        dj_dw += dj_dw_i 
    dj_dw = dj_dw / m 
    dj_db = dj_db / m 
        
    return dj_dw, dj_db

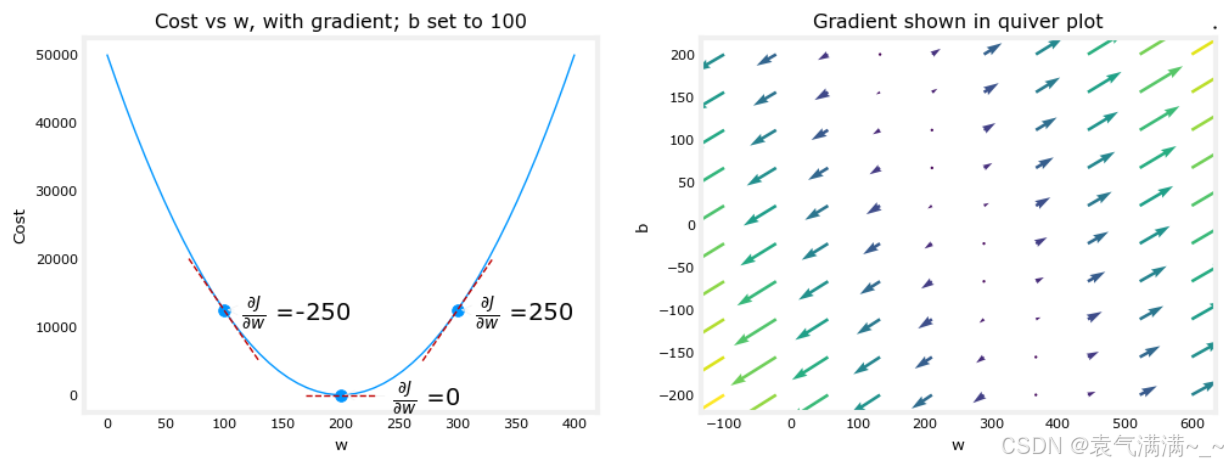
plt_gradients(x_train,y_train, compute_cost, compute_gradient)
plt.show()

# 梯度下降函数
def gradient_descent(x, y, w_in, b_in, alpha, num_iters, cost_function, gradient_function): 
    """
    Performs gradient descent to fit w,b. Updates w,b by taking 
    num_iters gradient steps with learning rate alpha
    
    Args:
      x (ndarray (m,))  : Data, m examples 
      y (ndarray (m,))  : target values
      w_in,b_in (scalar): initial values of model parameters  
      alpha (float):     Learning rate
      num_iters (int):   number of iterations to run gradient descent
      cost_function:     function to call to produce cost
      gradient_function: function to call to produce gradient
      
    Returns:
      w (scalar): Updated value of parameter after running gradient descent
      b (scalar): Updated value of parameter after running gradient descent
      J_history (List): History of cost values
      p_history (list): History of parameters [w,b] 
      """
    
    w = copy.deepcopy(w_in) # avoid modifying global w_in
    # An array to store cost J and w's at each iteration primarily for graphing later
    J_history = []
    p_history = []
    b = b_in
    w = w_in
    
    for i in range(num_iters):
        # Calculate the gradient and update the parameters using gradient_function
        dj_dw, dj_db = gradient_function(x, y, w , b)     

        # Update Parameters using equation (3) above
        b = b - alpha * dj_db                            
        w = w - alpha * dj_dw                            

        # Save cost J at each iteration
        if i<100000:      # prevent resource exhaustion 
            J_history.append( cost_function(x, y, w , b))
            p_history.append([w,b])
        # Print cost every at intervals 10 times or as many iterations if < 10
        if i% math.ceil(num_iters/10) == 0:
            print(f"Iteration {i:4}: Cost {J_history[-1]:0.2e} ",
                  f"dj_dw: {dj_dw: 0.3e}, dj_db: {dj_db: 0.3e}  ",
                  f"w: {w: 0.3e}, b:{b: 0.5e}")
 
    return w, b, J_history, p_history #return w and J,w history for graphing


# 初始化参数
w_init = 0
b_init = 0
iterations = 10000
tmp_alpha = 1.0e-2
w_final, b_final, J_hist, p_hist = gradient_descent(x_train ,y_train, w_init, b_init, tmp_alpha, iterations, compute_cost, compute_gradient)
print(f"(w,b) found by gradient descent: ({w_final:8.4f},{b_final:8.4f})")    # 找到最优值

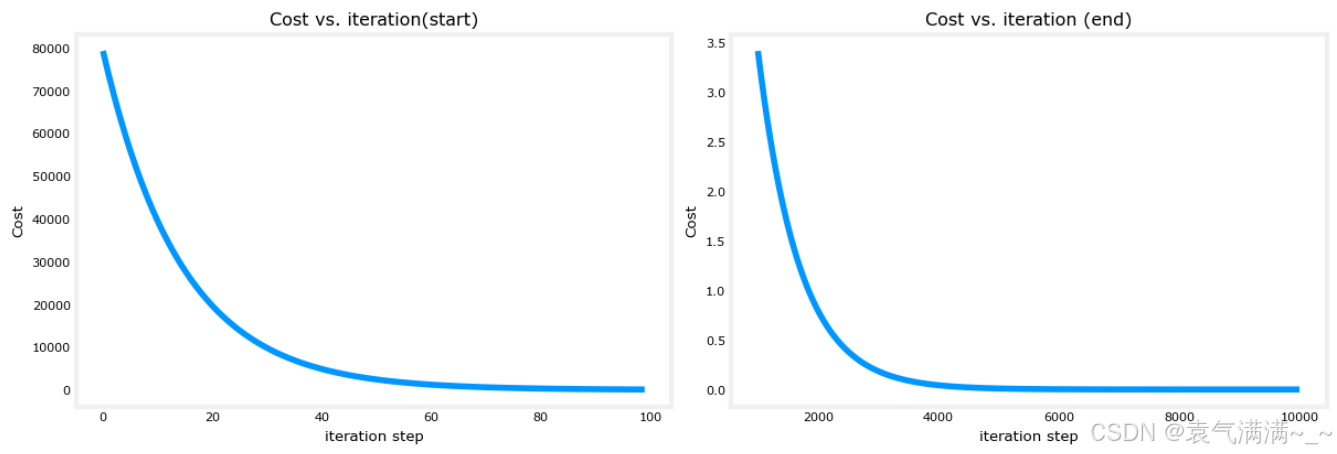
# 绘制成本与迭代次数的关系
fig, (ax1, ax2) = plt.subplots(1, 2, constrained_layout=True, figsize=(12,4))
ax1.plot(J_hist[:100])
ax2.plot(1000 + np.arange(len(J_hist[1000:])), J_hist[1000:])
ax1.set_title("Cost vs. iteration(start)");  ax2.set_title("Cost vs. iteration (end)")
ax1.set_ylabel('Cost')            ;  ax2.set_ylabel('Cost') 
ax1.set_xlabel('iteration step')  ;  ax2.set_xlabel('iteration step') 
plt.show()

# 预测
print(f"1000 sqft house prediction {w_final*1.0 + b_final:0.1f} Thousand dollars")    # 1000 sqft house prediction 300.0 Thousand dollars
print(f"1200 sqft house prediction {w_final*1.2 + b_final:0.1f} Thousand dollars")    # 1200 sqft house prediction 340.0 Thousand dollars
print(f"2000 sqft house prediction {w_final*2.0 + b_final:0.1f} Thousand dollars")    # 2000 sqft house prediction 500.0 Thousand dollars

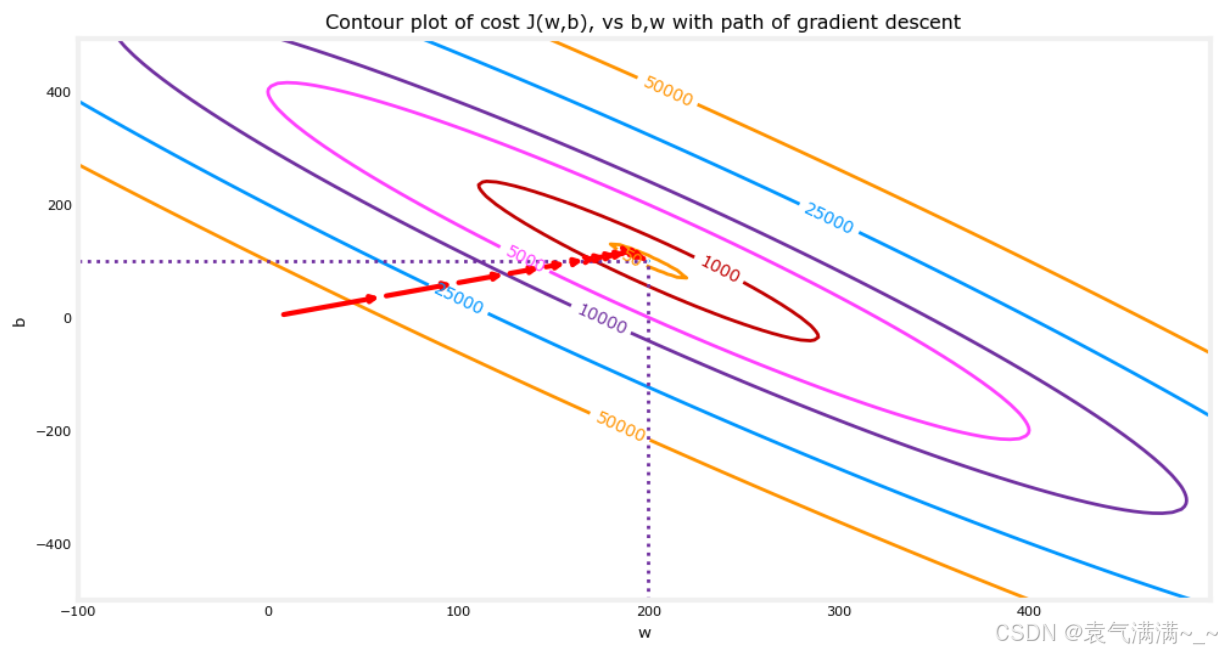
# 在成本（w，b）的等高线图上绘制迭代成本
fig, ax = plt.subplots(1,1, figsize=(12, 6))
plt_contour_wgrad(x_train, y_train, p_hist, ax)

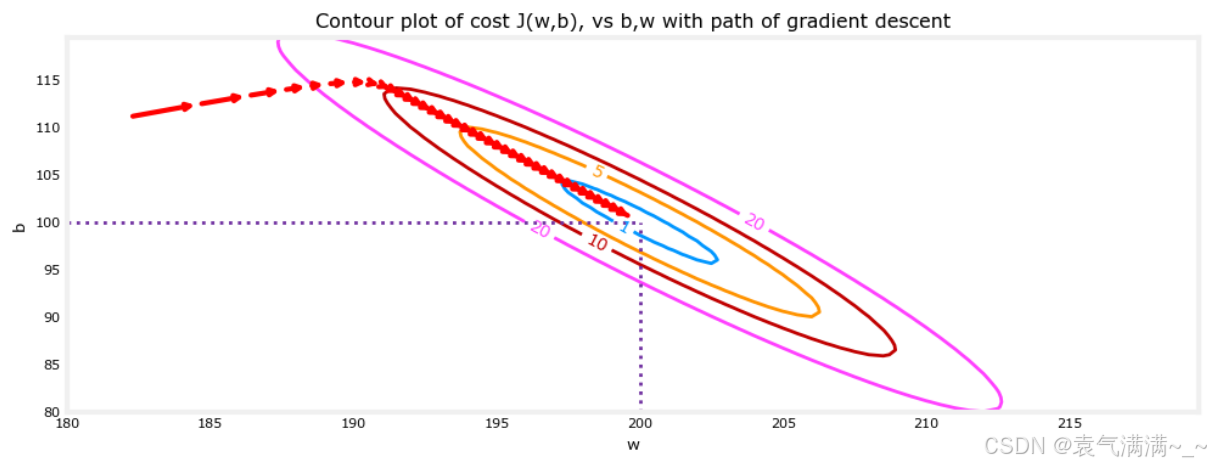
# 放大来看，梯度下降的最后几步，随着梯度趋近于零，步距缩短。
fig, ax = plt.subplots(1,1, figsize=(12, 4))
plt_contour_wgrad(x_train, y_train, p_hist, ax, w_range=[180, 220, 0.5], b_range=[80, 120, 0.5],contours=[1,5,10,20],resolution=0.5)

机器学习笔记

一、监督学习

1、监督学习定义

2、应用实例

3、监督学习的两种类型

3.1 回归（Regression）

3.2 分类（Classification）

二、无监督学习

1、无监督学习定义

2、类型

2.1 聚类（Clustering）

2.2 降维 (Dimensionality reduction)

2.3 异常检测 (Anomaly detection)

三、线性回归模型

1、回归模型 (Regression model)

2、模型的专业术语

3、模型训练和预测的流程

4、单变量线性回归**(Univariate linear regression)**

四、代价函数cost function

五、梯度下降

1、流程

2、实现

2.1 导数项

2.2 学习率 α

3、特性

3.1 在局部最小点停止更新

3.2 即使α固定，更新步长也会自动变小

4、线性回归的梯度下降

4.1 工作原理

4.2 批量梯度下降（batch gradient descent）

六、多元线性回归

1、符号表示

2、模型表示

2.1 向量化表示

3、梯度下降

4、正规方程

七、特征缩放

1、方法

1.1 最大值归一化

1.2 均值归一化

1.3 Z-score归一化

2、经验法则

八、逻辑回归

1、逻辑回归与分类问题

2、Sigmoid/Logistic 函数

3、模型表示

4、决策边界

4.1 线性决策边界

4.2 非线性决策边界

5、代价函数

九、过拟合与欠拟合

十、正则化

1、带正则化的代价函数

2、正则化线性回归与正则化逻辑回归

十一、相关练习

4、单变量线性回归(Univariate linear regression)