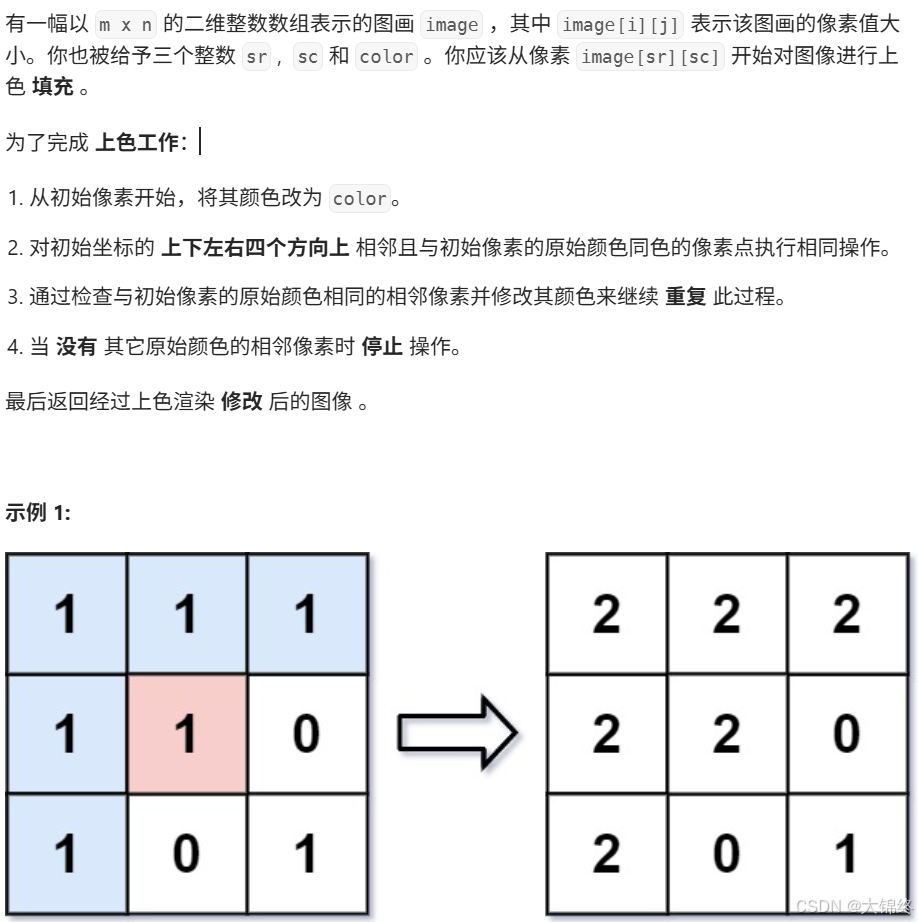
1. (733.) 图像渲染
思路:
从起始位置,在二维矩阵中进行深搜,利用向量数组表示该位置四周方向,用prev变量提前记录原位置颜色,边界条件判断若初始位置颜色等于color证明不用dfs直接返回即可,否则以此位置只要满足原始颜色等于prev就进行深搜。
cpp
class Solution {
int dx[4]={0,0,-1,1};//记录上下左右四个方向的变化量
int dy[4]={1,-1,0,0};
int prev;//保存原始颜色
int m,n;
public:
vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int color) {
m=image.size();
n=image[0].size();
if(image[sr][sc]==color) return image;//边界条件处理
else prev=image[sr][sc];
dfs(image,sr,sc,color);
return image;
}
void dfs(vector<vector<int>>& image, int a, int b, int color)
{
image[a][b]=color;
for(int i=0;i<4;i++)
{//以原坐标为基准来更新变量,要在临时变量上修改,否则会修改原基准坐标
int x=a+dx[i];
int y=b+dy[i];
if(x>=0&&x<m&&y<n&&y>=0&&image[x][y]==prev) dfs(image,x,y,color);
}
return;
}
};2. (200.) 岛屿数量

思路:
通过dfs在二维矩阵找到每一块相连的1的数量,关键要用到vis数组来标记每个对应位是否被使用过,避免重复计算。通过遍历矩阵,从每一个为1的位置进行dfs,dfs的作用是将从该位置起相连的1都设置为使用过。vis数组可以直接根据给定范围来开辟,也可以先用vector定义,初始化时设置为固定空间能节约一点空间
cpp
class Solution {
int dx[4]={0,0,1,-1};
int dy[4]={1,-1,0,0};
bool v[300][300];
int ret=0;
int m,n;
public:
int numIslands(vector<vector<char>>& grid) {
m=grid.size(),n=grid[0].size();
for(int i=0;i<m;i++)
{
for(int j=0;j<n;j++)
{
if(grid[i][j]=='1'&&!v[i][j])
{
dfs(grid,i,j);//调用函数
ret++;//岛屿数量增加
}
}
}
return ret;
}
void dfs(vector<vector<char>>& grid,int a,int b)
{
v[a][b]=true;
for(int i=0;i<4;i++)
{
int x=a+dx[i],y=b+dy[i];
if(x>=0&&x<m&&y>=0&&y<n&&grid[x][y]=='1'&&!v[x][y])//剪枝
{
dfs(grid,x,y);
}
}
return;
}
};3. (695.) 岛屿的最大面积

思路:
利用count全局变量或局部引用来记录每一次dfs后一块岛屿的面积,每次返回后更新最大值,注意每一块岛屿计算面积开始dfs前count都要置0
cpp
class Solution {
int dx[4]={0,0,1,-1};
int dy[4]={1,-1,0,0};
int m,n;
int ret=0;//记录最大面积
bool v[50][50];
public:
int maxAreaOfIsland(vector<vector<int>>& grid) {
m=grid.size(),n=grid[0].size();
int count=0;//引用保证局部共享,不是全局共享(全局变量)
for(int i=0;i<m;i++)
{
for(int j=0;j<n;j++)
{
if(grid[i][j]==1&&!v[i][j])
{
dfs(grid,i,j,count);
ret=max(ret,count);
count=0;//重置面积。每次都是从0累加计算
}
}
}
return ret;
}
void dfs(vector<vector<int>>& grid,int i,int j,int& count)
{
v[i][j]=true;
count++;
for(int k=0;k<4;k++)
{
int x=i+dx[k],y=j+dy[k];
if(x>=0&&x<m&&y>=0&&y<n&&grid[x][y]==1&&!v[x][y])
{
dfs(grid,x,y,count);
}
}
}
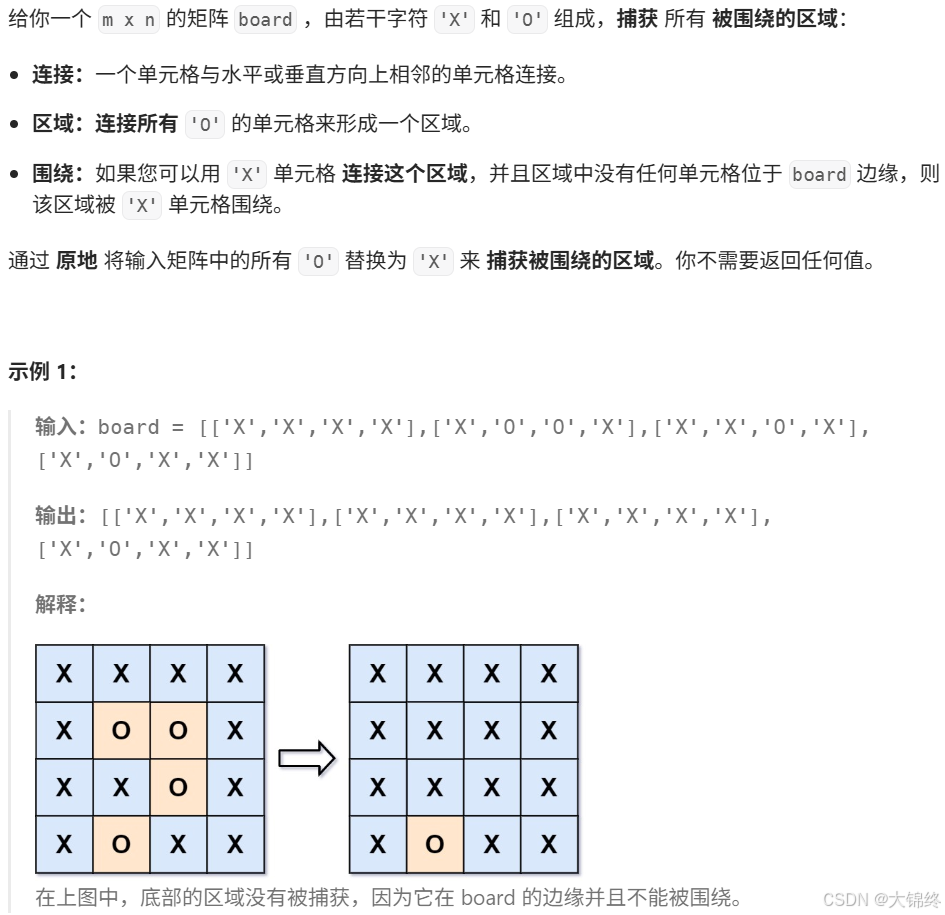
};4. (130.) 被围绕的区域
思路:
由于要处理与边界相连的岛屿,所以直接dfs比较困难,采取正难则反的思想,还是利用vis数组先处理与边界相连的岛屿,利用dfs这里的作用是将岛屿中单元格在vis数组中标记为已被使用,完后再对整个矩阵进行遍历,此时根据vis数组对所有岛屿所对应的单元格进行修改就没有问题
cpp
class Solution {
int dx[4]={0,0,1,-1};
int dy[4]={1,-1,0,0};
bool v[200][200];
int m,n;
public:
void solve(vector<vector<char>>& board) {
m=board.size(),n=board[0].size();
//先处理边界上相连的岛屿
for(int i=0;i<m;i++)//首尾两列
{
if(board[i][0]=='O'&&!v[i][0]) dfs(board,i,0);
if(board[i][n-1]=='O'&&!v[i][n-1]) dfs(board,i,n-1);
}
for(int i=1;i<n-1;i++)//首尾两行
{
if(board[0][i]=='O'&&!v[0][i]) dfs(board,0,i);
if(board[m-1][i]=='O'&&!v[m-1][i]) dfs(board,m-1,i);
}
//处理被包围的岛屿
for(int i=1;i<m-1;i++)
{
for(int j=1;j<n-1;j++)
{
if(board[i][j]=='O'&&!v[i][j])
{
board[i][j]='X';
}
}
}
}
void dfs(vector<vector<char>>& board,int a,int b)
{
v[a][b]=true;
for(int i=0;i<4;i++)
{
int x=a+dx[i],y=b+dy[i];
if(x>=0&&x<m&&y>=0&&y<n&&board[x][y]=='O'&&!v[x][y])
{
dfs(board,x,y);
}
}
}
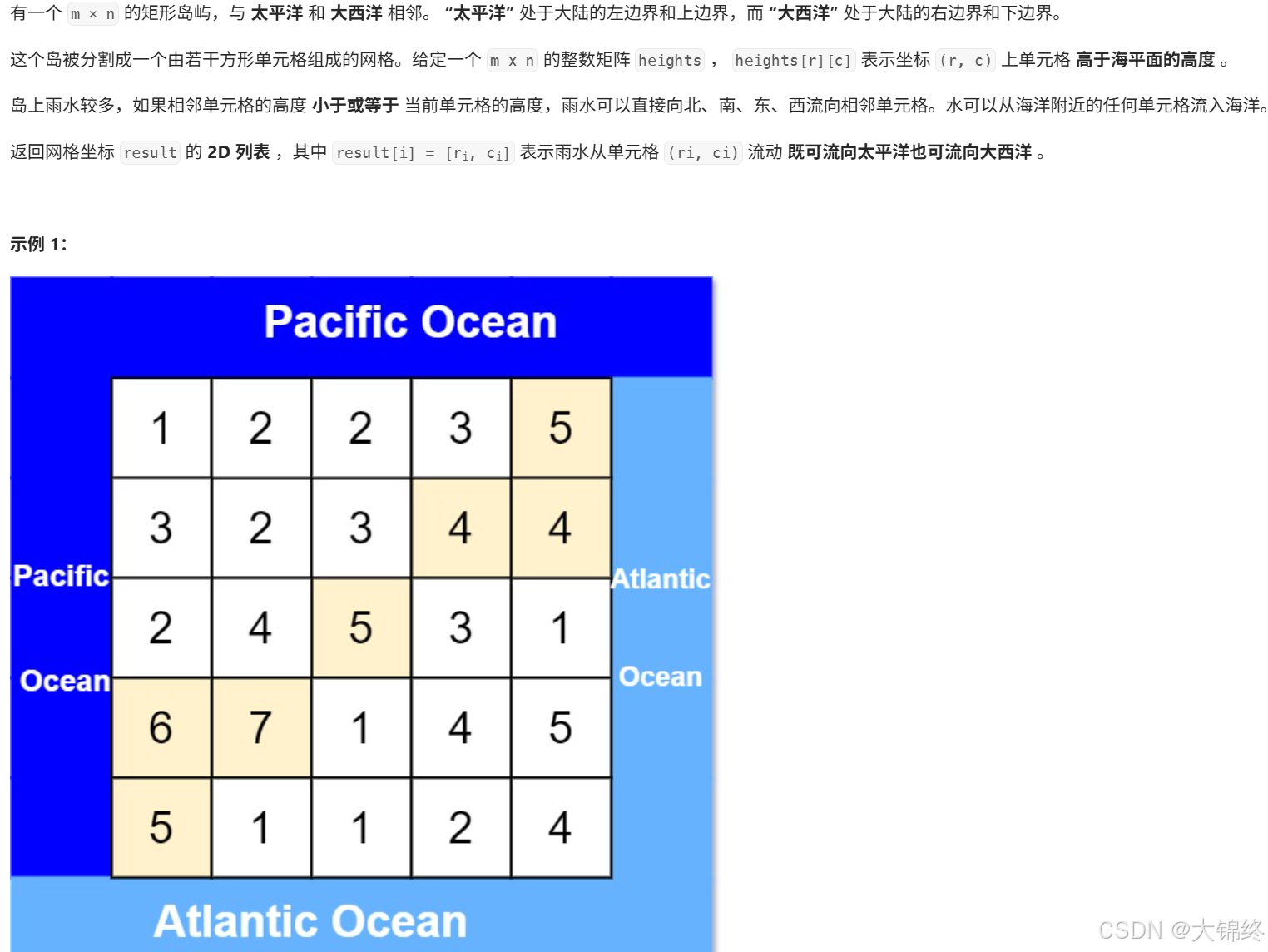
};5. (417.) 太平洋大西洋水流问题
思路:
如果直接暴力计算每一个位置能否到两洋,那么存在路径重复判断计算的可能,比较复杂。所以采取正难则反的思想,从两洋的沿岸反向dfs,就能找到哪些点可以流到两洋,最终被标记两次的点就是结果。
注意这里要用到两个vis标记数组,最好开固定大小作为参数传入
cpp
class Solution {
vector<vector<int>> ret;//最终返回结果
int dx[4]={1,-1,0,0};
int dy[4]={0,0,1,-1};
int m,n;
public:
vector<vector<int>> pacificAtlantic(vector<vector<int>>& heights) {
m=heights.size(),n=heights[0].size();
vector<vector<bool>> vis1(m,vector<bool>(n,0));
vector<vector<bool>> vis2(m,vector<bool>(n,0));
for(int i=0;i<m;i++)
{
//太平洋的水能从岛屿流到哪里
dfs(heights,i,0,vis1);
dfs(heights,i,n-1,vis2);
}
for(int i=0;i<n;i++)
{
//大西洋的水能从岛屿流到哪里
dfs(heights,0,i,vis1);
dfs(heights,m-1,i,vis2);
}
//遍历两个vis数组,结果都为true的加入结果数组中返回
for(int i=0;i<m;i++)
for(int j=0;j<n;j++)
{
if(vis1[i][j]&&vis2[i][j]) ret.push_back({i,j});
}
return ret;
}
void dfs(vector<vector<int>>& heights,int i,int j,vector<vector<bool>>&vis)
{
vis[i][j]=true;
for(int k=0;k<4;k++)
{
int x=i+dx[k],y=j+dy[k];
if(x>=0&&x<m&&y>=0&&y<n&&!vis[x][y]&&heights[i][j]<=heights[x][y])
{
dfs(heights,x,y,vis);
}
}
return;
}
};6. (529.) 扫雷游戏

思路:
二维矩阵的dfs,与前面题的区别在于遍历四个方向变为8个方向,加上了斜对角线,所以向量数组要存储八个元素。本题重点是理解扫雷的规则,本质是一道模拟类型的dfs
cpp
class Solution {
int m,n;
int dx[8]={0,0,1,-1,1,1,-1,-1};
int dy[8]={1,-1,0,0,1,-1,1,-1};
public:
vector<vector<char>> updateBoard(vector<vector<char>>& board, vector<int>& click) {
m=board.size(),n=board[0].size();
if(board[click[0]][click[1]]=='M'){
board[click[0]][click[1]]='X';
return board;
}
dfs(board,click[0],click[1]);
return board;
}
void dfs(vector<vector<char>>& board,int i,int j)
{
//统计地雷个数
int count=0;
for(int k=0;k<8;k++)
{
int x=i+dx[k],y=dy[k]+j;
if(x>=0&&x<m&&y>=0&&y<n&&board[x][y]=='M') count++;
}
//情况2
if(count==0)//周围没有地雷
{
board[i][j]='B';
for(int k=0;k<8;k++)
{
int x=i+dx[k],y=dy[k]+j;
if(x>=0&&x<m&&y>=0&&y<n&&board[x][y]=='E')
{
dfs(board,x,y);
}
}
}
else{//周围有地雷
board[i][j]='0'+count;
return;
}
}
};7. 面试题 13. 机器人的运动范围

思路:
二维矩阵dfs,需要vis数组标记是否使用过,计算每个数的数位之和,当符合条件返回值++并进行dfs
cpp
class Solution {
int dx[4]={1,-1,0,0};
int dy[4]={0,0,1,-1};
int ret=0;
int num=0;//记录一个数的各数位之和
int c;
vector<vector<bool>> vis;
public:
int wardrobeFinishing(int m, int n, int cnt) {
c=cnt;
vis.assign(m,vector<bool>(n,0));
dfs(0,0,m,n);
return ret;
}
void dfs(int i, int j,int m, int n)
{
vis[i][j]=true;
num=0;//每次刷新
int p=i,q=j;//避免原始值被修改
for(int k=0;k<3;k++)
{//最大是三位数
num+=(p%10+q%10);
p/=10;
q/=10;
}
if(num>c) return;
else{
ret++;
for(int k=0;k<4;k++)
{
int x=i+dx[k],y=j+dy[k];
if(x>=0&&x<m&&y>=0&&y<n&&!vis[x][y]) dfs(x,y,m,n);
}
}
}
};