聚类算法概述
聚类是机器学习中一种重要的无监督学习方法,其目标是在没有先验标签的情况下,根据样本之间的相似性,将数据自动划分为若干类别。聚类结果通常要求同一类内部的数据相似度较高,而不同类别之间的差异尽可能大。由于不依赖人工标注,聚类算法在数据探索、模式识别和异常检测等领域具有广泛应用。
聚类的基本概念
在聚类任务中,每一个数据对象通常被表示为一个特征向量,样本之间的相似性或距离是划分聚类的重要依据。常用的距离度量方法包括欧氏距离、曼哈顿距离以及余弦相似度等。
聚类的核心思想可以概括为"类内相似、类间差异",即同一簇内的数据点在特征空间中相互接近,而不同簇之间的数据点相对较远。
需要注意的是,聚类结果往往不唯一,不同的算法或参数设置可能得到不同的聚类划分,因此在实际应用中需要结合具体任务需求对结果进行分析与评估。
常见聚类算法简介
根据聚类思想的不同,常见的聚类算法主要可以分为基于划分的方法、基于层次的方法以及基于密度的方法。
K-means 聚类算法
K-means 是一种经典的基于划分的聚类算法,其基本思想是将数据划分为预先指定数量
𝐾
K 个簇。算法通过不断迭代,将每个样本分配给距离最近的聚类中心,并更新聚类中心的位置,直到收敛为止。
K-means 算法实现简单、计算效率高,适用于处理大规模数据集。然而,该算法需要事先指定簇的数量,对初始中心点较为敏感,并且难以识别非球形结构的数据和噪声点。
层次聚类算法
层次聚类通过逐步合并或分裂簇的方式构建聚类结构,最终形成一棵层次树(树状图)。根据构建方式的不同,层次聚类可分为自底向上的凝聚型聚类和自顶向下的分裂型聚类。
层次聚类不需要预先指定聚类数量,能够直观地展示数据之间的层次关系,但其计算复杂度较高,在处理大规模数据时效率较低。
密度聚类算法
密度聚类算法基于数据分布的密度特征进行聚类,其核心思想是:同一簇中的样本在特征空间中具有较高的密度,而不同簇之间由低密度区域分隔。
与 K-means 等算法相比,密度聚类方法能够识别任意形状的簇,并且对噪声具有较强的鲁棒性。
DBSCAN(Density-Based Spatial Clustering of Applications with Noise)是最具代表性的密度聚类算法之一,也是本文后续重点介绍的对象。
DBSCAN 算法基本思想
DBSCAN(Density-Based Spatial Clustering of Applications with Noise)是一种基于密度的聚类算法,其核心思想是通过样本点在特征空间中的分布密度来发现聚类结构。算法认为:簇是由高密度区域组成,不同簇之间由低密度区域分隔。
DBSCAN 通过两个关键参数来刻画密度特征:
ε(eps):邻域半径
MinPts:最小样本数
ε-邻域的定义
对于数据集中的任意样本点 其 ε-邻域定义为距离不超过 ε 的所有样本点集合:
N_ε(x_i) = { x_j | dist(x_i, x_j) ≤ ε }
其中,dist(·) 表示样本之间的距离度量,常用欧氏距离:
dist(x_i, x_j) = sqrt( Σ_k (x_i^k - x_jk)2 )
核心点、边界点与噪声点
根据 ε-邻域中样本点的数量,DBSCAN 将数据点划分为以下三类:
1. 核心点(Core Point)
若样本点 的 ε-邻域中包含的点数不少于 MinPts,则该点为核心点:
|N_ε(x_i)| ≥ MinPts
2. 边界点(Border Point)
若样本点本身不是核心点,但位于某个核心点的 ε-邻域内,则该点称为边界点:
|N_ε(x_i)| < MinPts
且 ∃ 核心点 x_k,使得 x_i ∈ N_ε(x_k)
3. 噪声点(Noise Point)
既不是核心点,也不属于任何核心点 ε-邻域的点,被视为噪声点:
x_i 既不是核心点,也不是边界点
密度可达(Density-Reachable)
给定两个样本点 xi 和 xj,若存在一条点序列:
xi = p1, p2, ..., pn = xj
使得对任意 k (1 ≤ k < n),均满足:
p(k+1) ∈ N_eps(p(k))
并且 p(k) 为核心点(除最后一个点外),
则称样本点 xj 是从 xi 密度可达的(density-reachable)。
需要注意的是,密度可达关系是非对称的。
也就是说,xj 从 xi 密度可达,并不一定意味着 xi 从 xj 密度可达。
密度相连(Density-Connected)
若存在某个样本点 xk,使得样本点 xi 和 xj 都从 xk 密度可达,则称 xi 与 xj 密度相连(density-connected)。
其形式化描述为:
存在 xk,使得:
xi 是从 xk density-reachable
xj 是从 xk density-reachable
密度相连关系是对称的,也是 DBSCAN 中定义聚类的重要依据。
如果一组样本点两两之间密度相连,则这些样本点属于同一个聚类。
总结为一张图
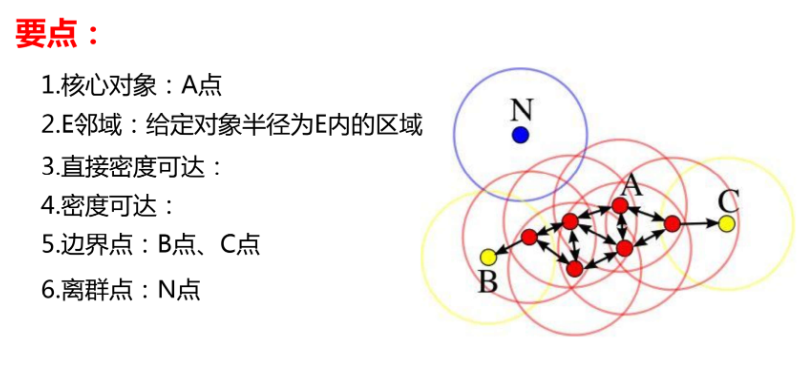
DBSCAN 聚类定义
DBSCAN 将满足以下条件的一组样本点定义为一个簇:
任意两个样本点在该簇中是密度相连的
簇内样本点的最大集合满足密度可达性
DBSCAN 算法实现过程
DBSCAN 算法通过不断扩展高密度区域来形成聚类,其核心过程是从核心点出发,将密度可达的样本点逐步合并为同一个簇,并将无法归入任何簇的样本视为噪声点。算法整体流程如下。
算法输入参数
数据集 D = {x1, x2, ..., xn}
邻域半径 eps
最小样本数 MinPts
算法执行步骤
步骤 1:初始化
将所有样本点标记为"未访问"
簇编号 cluster_id = 0
步骤 2:遍历数据集中的每一个样本点 xi
如果 xi 已访问,则跳过
否则,将 xi 标记为已访问
步骤 3:计算 eps 邻域
计算 N_eps(xi) = { xj | dist(xi, xj) ≤ eps }
步骤 4:判断是否为核心点
如果 |N_eps(xi)| < MinPts:
将 xi 标记为噪声点
继续处理下一个样本点
如果 |N_eps(xi)| ≥ MinPts:
xi 为核心点
cluster_id = cluster_id + 1
创建一个新簇 C(cluster_id)
将 xi 加入该簇
步骤 5:扩展簇(密度扩展过程)
将 N_eps(xi) 中的所有点加入一个队列 Q
当 Q 非空时:
取出队首元素 xk
如果 xk 未访问:
将 xk 标记为已访问
计算 N_eps(xk)
如果 |N_eps(xk)| ≥ MinPts:
将 N_eps(xk) 中的点加入 Q
如果 xk 尚未被分配到任何簇:
将 xk 加入当前簇 C(cluster_id)
步骤 6:继续遍历剩余样本点
重复步骤 2 ~ 步骤 5
直到所有样本点都被访问
算法输出
若干个聚类簇 C1, C2, ..., Ck
以及被标记为噪声的样本点集合
过程说明
每个簇一定从核心点开始
通过核心点不断"向外扩展",吸收密度可达的样本
边界点可以被吸收进簇,但不能继续扩展
无法归入任何簇的点被视为噪声
可总结为以下三点

DBSCAN 算法的优缺点
优点
无需预先指定簇的数量
DBSCAN 不需要像 K-means 算法那样事先设定聚类的簇数,能够根据数据的实际分布自动发现聚类结构,减少了人工干预。
能够识别任意形状的簇
由于基于密度进行聚类,DBSCAN 不依赖于簇的几何形状,能够有效识别非球形、非规则分布的数据簇,在复杂数据分布场景中表现良好。
对噪声和异常点具有较强的鲁棒性
DBSCAN 可以将密度较低、无法归入任何簇的样本点直接标记为噪声点,这使得算法在存在异常数据的情况下仍能保持较好的聚类效果。
适合无监督数据分析任务
在无需标签信息的前提下,DBSCAN 能够完成聚类划分,适用于数据探索、异常检测等无监督学习场景。
缺点
对参数 eps 和 MinPts 较为敏感
不同的参数组合可能导致完全不同的聚类结果,参数选择不当时,容易出现簇被合并或过度分割的情况。
难以处理密度差异较大的数据集
当不同簇的密度差异较大时,使用统一的 eps 参数往往难以同时适配所有簇,可能导致部分簇无法被正确识别。
在高维数据中效果可能下降
随着数据维度的增加,样本点之间的距离趋于相似,密度概念变得不明显,从而影响 DBSCAN 的聚类效果。
计算复杂度受数据规模影响较大
在未使用高效空间索引结构的情况下,DBSCAN 需要频繁计算样本间距离,当数据规模较大时,计算开销较高。