平衡二叉树的引入
之前我们学习过二叉搜索树,发现在二叉搜索树中,存在以下问题,当每次插入的元素都比当前大,二叉搜索树就会退化成为链表,查找的时间复杂度就会退化成为O(N),比如下面的
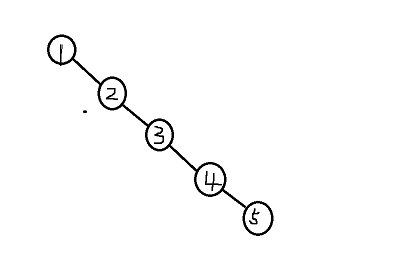
于是我们引入平衡二叉树(AVL树),平衡二叉树具有以下特性
它的左右子树都是AVL树
左右子树高度之差(简称平衡因子)的绝对值不超过1
平衡二叉树的定义
cpp
template<class T>
class AVLTreeNode
{
public:
AVLTreeNode(const T& data)
:_val(data)
,_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_bf(0)
{
}
int _bf; //平衡因子
T _val;
AVLTreeNode<T>* _left;
AVLTreeNode<T>* _right;
AVLTreeNode<T>* _parent;
};
template<class T>
class AVLTree
{
typedef AVLTreeNode<T> Node;
private:
Node _root;
};平衡因子在我们的实现里面默认为右子树的高度减去左边子树的高度
AVL树的插入
在AVL树的各种操作当中,最重要的就是AVL树的插入操作,二叉树的插入操作步骤:
1.按照二叉搜索树的插入去实现
2.调整二叉树的各个节点的平衡因子
3.一旦某个节点的的平衡因子超过规定,就调整二叉树
cpp
bool insert(const T& val)
{
if (_root == nullptr)
{
_root = new Node(val);
return true;
}
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (cur->_val < val)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_val > val)
{
parent = cur;
cur = cur->_left;
}
else return false;
}
cur = new Node(val);
if (val > parent->_val)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
cur->_parent = parent; //前面的代码是二叉搜索树的插入实现
//更新平衡因子
while (parent)
{
if (cur ==parent->_right)
{
parent->_bf++;
}
else parent->_bf--;
if (parent->_bf == 0) break;
else if (parent->_bf == 1 || parent->_bf == -1)
{
cur = parent;
parent = parent->_parent;
}
else if (parent->_bf == 2 || parent->_bf == -2)
{
//做各种旋转处理
if (parent->_bf == 2 && cur->_bf == 1)
{
//左单旋转
}
else if (parent->_bf == -2 && cur->_bf == -1)
{
//右单旋转
}
else if (parent->_bf == 2 && cur->_bf == -1)
{
//先右再左边
}
else if (parent->_bf == -2 && cur->_bf == 1)
{
//先左再右边
}
break;
}
else assert(false); //说明之前出错了,没有来得及处理,现在直接报错
}
return true;
}关于更新平衡因子
插入之后,如果是插入在父亲节点的右边,那么父亲节点的平衡因子就需要加1,因为这里平衡因子的计算是右子树的高度减去左子树的高度,插在右边必然让右子树的高度加1
相反,如果是左边,必然平衡因子要减去1
cpp
//更新平衡因子
while (parent)
{
if (cur ==parent->_right)
{
parent->_bf++;
}
else parent->_bf--;
if (parent->_bf == 0) break;
else if (parent->_bf == 1 || parent->_bf == -1)
{
cur = parent;
parent = parent->_parent;
}
else if (parent->_bf == 2 || parent->_bf == -2)
{
}
else assert(false); //说明之前出错了,没有来得及处理,现在直接报错
}情况1
插入之后,如果父节点的平衡因子变成0了,就不需要往上面更新,比如下面的
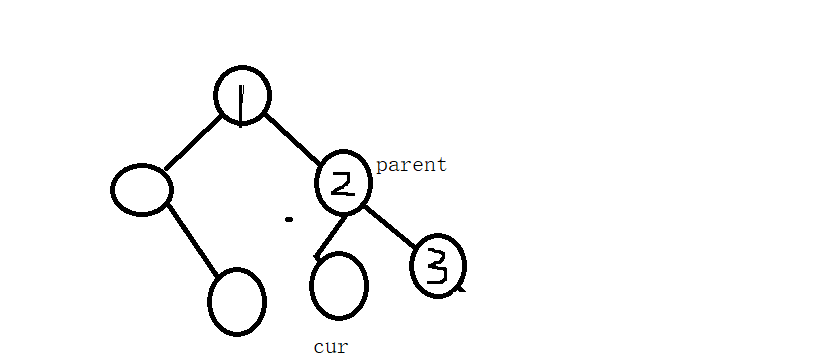
该树的的每个节点的平衡因子都是和插入之前该树的每个节点的平衡因子,除了parent的平衡因子需要改变一下
情况2
如果更新后的parent的平衡因子为1或-1,就需要往上更新了,比如下面的
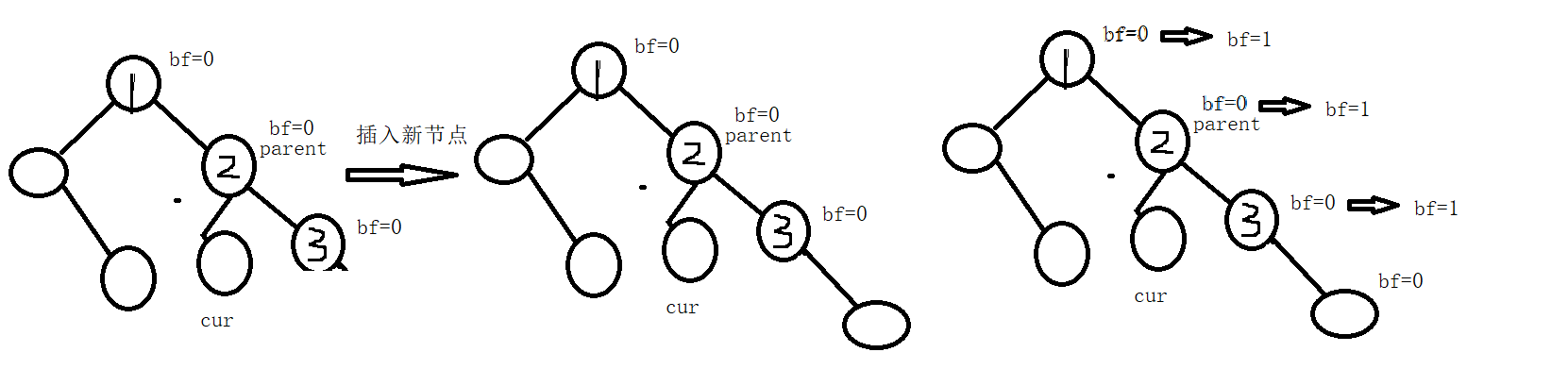
情况3
如果更新后节点的平衡因子大于1或小于-1,那么就需要旋转操作,让其符合AVL树的规定,情况一共有四种,分别如下:
RR
插入在了parent节点的右子树的右边,比如下面的
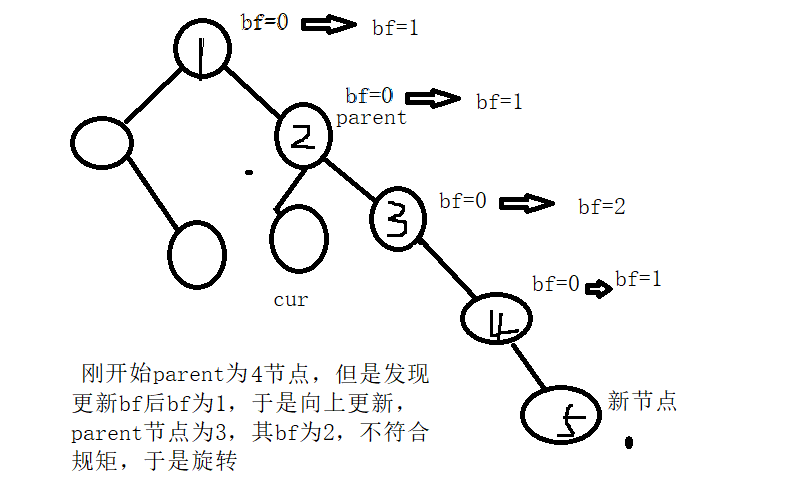
这个时候我们需要左旋父亲节点,下面我用一个抽象图来分析,以便符合所有情况
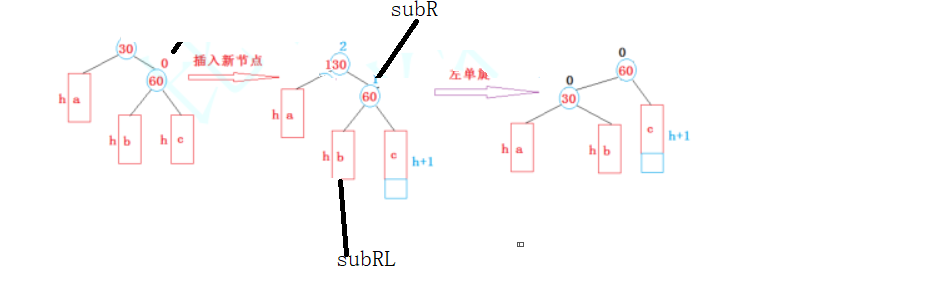
让subR(可能为空)变成parent的左边节点,parent变成subR的左孩子
cpp
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
parent->_right = subRL;
if (subRL) //如果不为空,其父亲指向parent
subRL->_parent = parent;
Node* ParentParent = parent->_parent;
subR->_left = parent;
parent->_parent = subR;
if (ParentParent == nullptr) 父亲的父亲为空,让subR为根节点
{
_root = subR;
subR->_parent = nullptr;
}
else
{
if (parent == ParentParent->_left)
{
ParentParent->_left = subR;
subR->_parent = ParentParent;
}
else
{
ParentParent->_right = subR;
subR->_parent = ParentParent;
}
}
subR->_bf = parent->_bf = 0; //更新平衡因子
}LL
插入在了parent节点的左子树的左边
抽象图
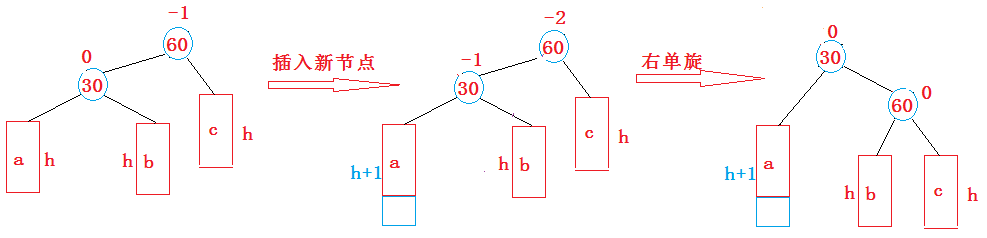
分析同RR一样
cpp
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left = subLR;
if (subLR)
subLR->_parent = parent;
Node* ParentParent = parent->_parent;
subL->_right = parent;
parent->_parent = subL;
if (ParentParent == nullptr)
{
_root = subL;
subL->_parent = nullptr;
}
else
{
if (parent == ParentParent->_left)
{
ParentParent->_left = subL;
subL->_parent = ParentParent;
}
else
{
ParentParent->_right = subL;
subL->_parent = ParentParent;
}
}
subL->_bf = parent->_bf = 0;
}RL
插在了parent的右子树的左边,导致不平衡,这个时候需要先右旋subR,再左旋parent节点
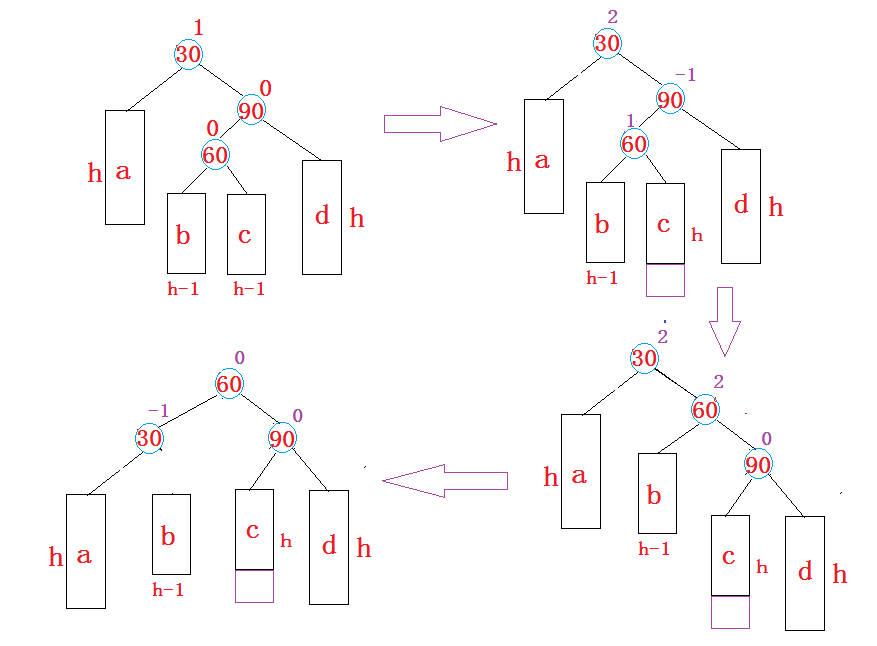
上面可能插在b,也可能插在c,导致最后的各个节点的平衡因子发生不一样的变化
cpp
void RotateRL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
int bf = subRL->_bf;
RotateR(parent->_right);
RotateL(parent);
if (bf == 0) //subRL为新插入的节点
{
parent->_bf = 0;
subR->_bf = 0;
subRL->_bf = 0;
}
else if (bf == 1)
{
parent->_bf = -1;
subR->_bf = 0;
subRL->_bf = 0;
}
else if (bf == -1)
{
subR->_bf = 1;
parent->_bf = 0;
subRL->_bf = 0;
}
else
{
assert(false);
}
}LR
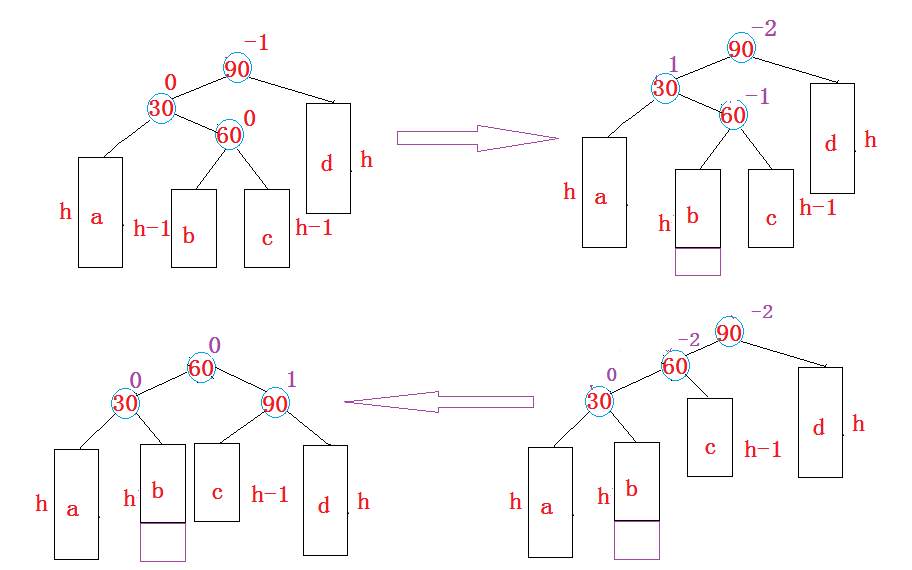
cpp
void RotateLR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
int bf = subLR->_bf;
RotateL(parent->_left);
RotateR(parent);
if (bf == 0)
{
parent->_bf = 0;
subL->_bf = 0;
subLR->_bf = 0;
}
else if (bf == 1)
{
parent->_bf = 0;
subL->_bf = -1;
subLR->_bf = 0;
}
else if (bf == -1)
{
subL->_bf = 0;
parent->_bf = 1;
subLR->_bf = 0;
}
else assert(false);
}旋转总结:
RR:左旋parent
LL:右旋parent
RL:右旋parent->subR,再左旋parent
LR:左旋parent->subL,再右边旋parent
整体代码
cpp
#include<iostream>
#include<assert.h>
using namespace std;
template<class T>
class AVLTreeNode
{
public:
AVLTreeNode(const T& data)
:_val(data)
,_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_bf(0)
{
}
int _bf; //平衡因子
T _val;
AVLTreeNode<T>* _left;
AVLTreeNode<T>* _right;
AVLTreeNode<T>* _parent;
};
template<class T>
class AVLTree
{
typedef AVLTreeNode<T> Node;
public:
AVLTree() = default;
AVLTree& operator=(const AVLTree<T>& a)
{
swap(_root, a._root);
return *this;
}
AVLTree(const AVLTree<T>& t)
{
_root = Copy(t._root);
}
bool insert(const T& val)
{
if (_root == nullptr)
{
_root = new Node(val);
return true;
}
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (cur->_val < val)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_val > val)
{
parent = cur;
cur = cur->_left;
}
else return false;
}
cur = new Node(val);
if (val > parent->_val)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
cur->_parent = parent;
//更新平衡因子
while (parent)
{
if (cur ==parent->_right)
{
parent->_bf++;
}
else parent->_bf--;
if (parent->_bf == 0) break;
else if (parent->_bf == 1 || parent->_bf == -1)
{
cur = parent;
parent = parent->_parent;
}
else if (parent->_bf == 2 || parent->_bf == -2)
{
//做各种旋转处理
if (parent->_bf == 2 && cur->_bf == 1)
{
//左单旋转
RotateL(parent);
}
else if (parent->_bf == -2 && cur->_bf == -1)
{
//右单旋转
RotateR(parent);
}
else if (parent->_bf == 2 && cur->_bf == -1)
{
//先右再左边
RotateRL(parent);
}
else if (parent->_bf == -2 && cur->_bf == 1)
{
//先左再右边
RotateLR(parent);
}
break; //必须加,旋转完了之后,parent肯定不为空,树已经成为了AVL树
//这时候满足平衡二叉树,继续更新bf,会导致错误
}
else assert(false); //说明之前出错了,没有来得及处理,现在直接报错
}
return true;
}
T& root_val()
{
return _root->_val;
}
void inordered()
{
_MidOrdered(_root); //中序遍历,判断是否是二叉搜索树
}
bool IsBalanceTree() //判断是否为avl树
{
return _IsBalanceTree(_root);
}
private:
Node* Copy(Node* root)
{
if (root == nullptr)
return nullptr;
Node* newRoot = new Node(root->_val);
newRoot->_bf = root->_bf;
newRoot->_left = Copy(root->_left);
newRoot->_right = Copy(root->_right);
return newRoot;
}
int _height(Node* root)
{
if (root == nullptr) return 0;
else return 1 + max(_height(root->_left), _height(root->_right));
}
bool _IsBalanceTree(Node* root)
{
if (root == nullptr) return true;
int LeftHeight = _height(root->_left);
int RightHeight = _height(root->_right);
int diff = RightHeight - LeftHeight;
if (diff != root->_bf || (diff < -1 || diff>1))
{
return false;
}
return _IsBalanceTree(root->_left) && _IsBalanceTree(root->_right);
}
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
parent->_right = subRL;
if (subRL)
subRL->_parent = parent;
Node* ParentParent = parent->_parent;
subR->_left = parent;
parent->_parent = subR;
if (ParentParent == nullptr)
{
_root = subR;
subR->_parent = nullptr;
}
else
{
if (parent == ParentParent->_left)
{
ParentParent->_left = subR;
subR->_parent = ParentParent;
}
else
{
ParentParent->_right = subR;
subR->_parent = ParentParent;
}
}
subR->_bf = parent->_bf = 0;
}
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left = subLR;
if (subLR)
subLR->_parent = parent;
Node* ParentParent = parent->_parent;
subL->_right = parent;
parent->_parent = subL;
if (ParentParent == nullptr)
{
_root = subL;
subL->_parent = nullptr;
}
else
{
if (parent == ParentParent->_left)
{
ParentParent->_left = subL;
subL->_parent = ParentParent;
}
else
{
ParentParent->_right = subL;
subL->_parent = ParentParent;
}
}
subL->_bf = parent->_bf = 0;
}
void RotateRL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
int bf = subRL->_bf;
RotateR(parent->_right);
RotateL(parent);
if (bf == 0) //subRL为新插入的节点
{
parent->_bf = 0;
subR->_bf = 0;
subRL->_bf = 0;
}
else if (bf == 1)
{
parent->_bf = -1;
subR->_bf = 0;
subRL->_bf = 0;
}
else if (bf == -1)
{
subR->_bf = 1;
parent->_bf = 0;
subRL->_bf = 0;
}
else
{
assert(false);
}
}
void RotateLR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
int bf = subLR->_bf;
RotateL(parent->_left);
RotateR(parent);
if (bf == 0)
{
parent->_bf = 0;
subL->_bf = 0;
subLR->_bf = 0;
}
else if (bf == 1)
{
parent->_bf = 0;
subL->_bf = -1;
subLR->_bf = 0;
}
else if (bf == -1)
{
subL->_bf = 0;
parent->_bf = 1;
subLR->_bf = 0;
}
else assert(false);
}
void _MidOrdered(Node* root)
{
if (root == nullptr) return;
_MidOrdered(root->_left);
cout << root->_val << " ";
_MidOrdered(root->_right);
}
private:
Node* _root = nullptr;
};测试代码
cpp
int main()
{
AVLTree<int> A;
//vector<int> v = {4,2,6,1,3,5,15,7,16,14};
vector<int> v = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
for (auto e : v)
{
A.insert(e);
}
A.inordered(); cout << endl;
cout << A.IsBalanceTree() << endl;
return 0;
}
运行结果:
