数据结构第七章：查找

一、查找的基本概念（基础必懂）

✅ 查找的定义

• 在一个给定的数据集合中，找出满足某种条件的元素的过程。
• 每个元素都有一个关键字（Key），用于比较和定位。

✅ 分类方式

类型	特点
静态查找	查找过程中数据不变化，只支持查找操作 → 如顺序表、索引表
动态查找	支持插入、删除、查找操作 → 如二叉排序树、哈希表

✅ 效率指标：平均查找长度（ASL）

• ASL = 所有查找路径长度之和 / 总查找次数
• 查找成功 ASL：找到目标元素时的平均比较次数
• 查找失败 ASL：未找到时的平均比较次数

💡 考点：计算不同查找方法的 ASL

---

二、线性结构查找（重点掌握）

✅ （一）顺序查找

📌 算法思想：

• 从第一个元素开始，逐个比较，直到找到或遍历完

📌 步骤：

typedef struct { // 查找表的顺序结构（顺序表）
	ElemType *elem; // 动态数组基址
	int TableLen; // 表的长度
} SSTable;

int Search_Seq(SSTable ST, ElemType key) {
	ST.elem[0] = key; // 哨兵
	int i;
	for(i = ST.TableLen; ST.elem[i] != key; i--); // 从后往前找
	return i; // 若查找成功，则返回元素下标，查找失败则返回0
}

📌 时间复杂度：

• 最坏：O(n)
• 平均：ASL = (n+1)/2

📌 适用场景：

• 无序表、小规模数据

✅ 优点 ：简单，无需排序

❌ 缺点：效率低

---

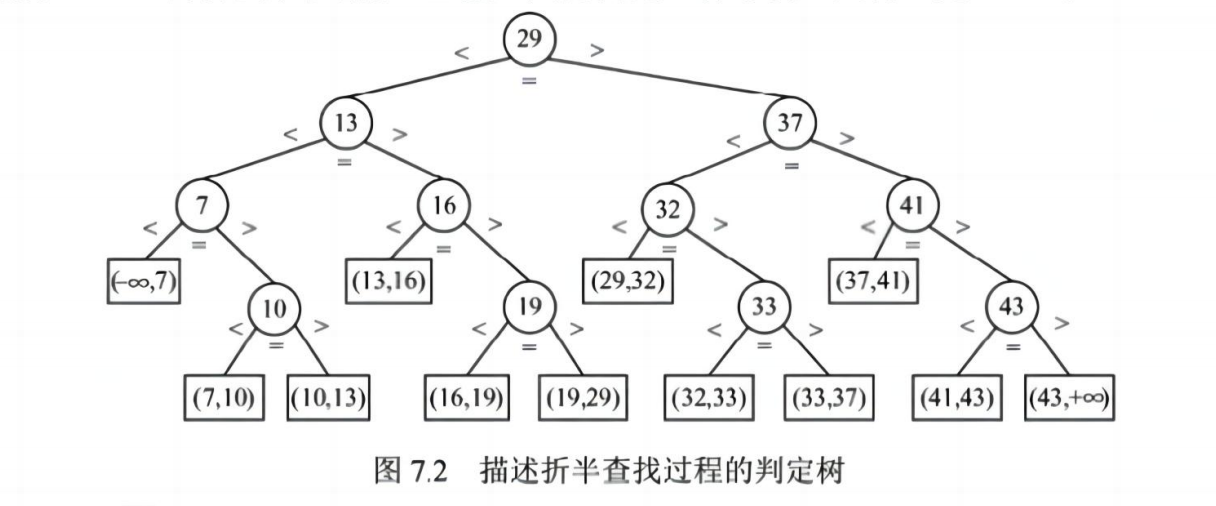
✅ （二）折半查找（二分查找）

📌 前提条件：

• 有序表（升序或降序）

📌 算法思想：

• 每次比较中间元素，根据大小决定在左半部分还是右半部分继续查找

📌 步骤：

typedef struct { // 查找表的顺序结构（顺序表）
	ElemType *elem; // 动态数组基址
	int TableLen; // 表的长度
} SSTable;

int Binary_Search(SSTable L, ElemType key) {
	int low = 0;
	int high = L.TableLen - 1;
	int mid;
	while(low <= high) {
		mid = (low + high) / 2; // 取中间位置
		if(key > L.elem[mid]) {
			low = mid + 1; // 从后半部分继续查找
		} else if(key < L.elem[mid]) {
			high = mid - 1; // 从前半部分继续查找
		} else {
			return mid; // 查找成功则返回所在位置
		}
	}
	return -1; // 查找失败，返回-1
}

📌 时间复杂度：

• 
• 查找成功 ASL ≈

📌 构造判定树：

• 将查找过程画成一棵二叉树，每个节点为比较值
• 叶子节点表示查找失败位置

💡 考点：手写折半查找过程、构造判定树、计算 ASL

---

✅ （三）分块查找

📌 思想：

• 将有序表分为若干块，每块内无序，但块间有序
• 先在块索引中用折半查找确定目标块，再在块内顺序查找

📌 步骤：

1. 在索引表中折半查找目标块
2. 在该块内顺序查找

📌 时间复杂度：

• 
• 块数 ，每块约 个元素

✅ 优点 ：比顺序查找快，比折半查找灵活

❌ 缺点：需要额外空间存储索引
💡 考点：理解分块查找原理，能估算 ASL

---

三、树形结构查找（重中之重！）

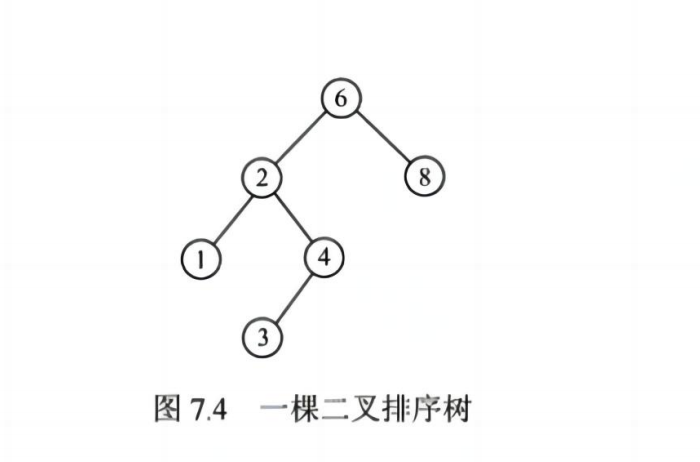
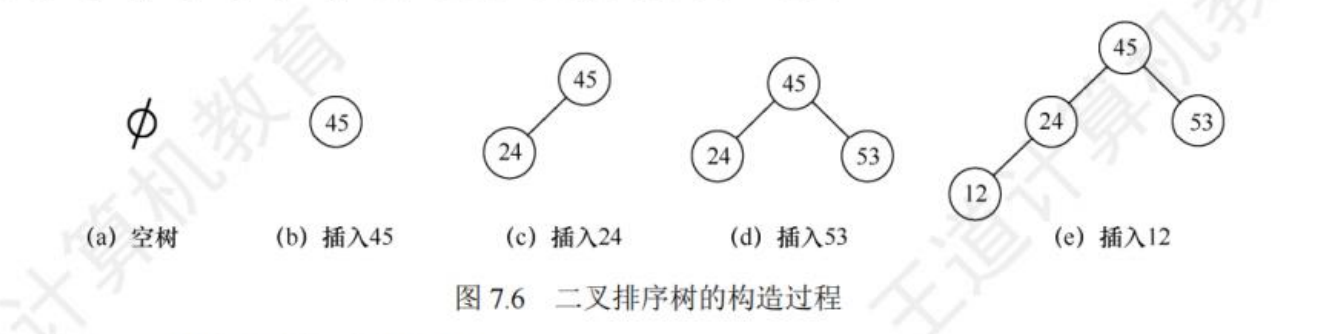
✅ （一）二叉排序树（BST）

📌 定义：

• 左子树所有节点 < 根节点 < 右子树所有节点
• 是一种动态查找表

// 构造二叉排序树
void Create_BST(BiTree &T, KeyType str[], int n) {
	T = NULL;
	int i = 0;
	while(i < n) {  // 依次将每个关键字插入二叉树
		BST_Insert(T, str[i++]);
	}
}

📌 操作：

• 查找：类似折半查找

typedef struct BSTNode {
	ElemType data; // 数据域
	struct BSTNode *lchild, *rchild; // 左、右孩子指针
} BSTNode, *BiTree;

BSTNode *BST_Search(BiTree T, ElemType key) {
	while(T != NULL && key != T -> data) { // 若树空或等于根结点值，则结束循环
		if(key < T -> data) { // 小于，则在左子树上查找
			T = T -> lchild;
		} else { // 大于，则在右子树上查找
			T = T -> rchild;
		}
	}
	return T;
}

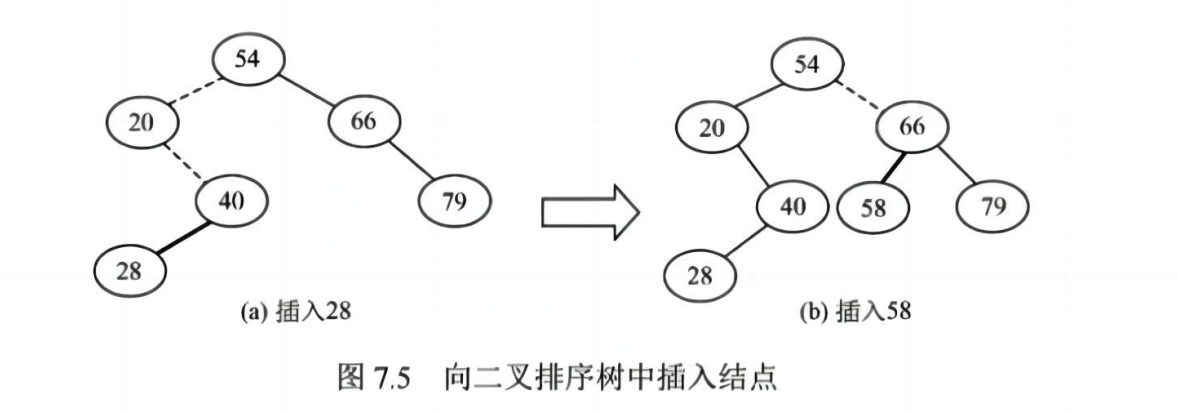
• 插入：从根开始，按大小关系插入合适位置

// 二叉排序树插入
int BST_Insert(BiTree &T, ElemType key) {
    if(T == NULL) { // 原树为空，新插入的根结点记为根结点
        T = new BSTNode();
        T -> data = key;
        T -> lchild = NULL;
        T -> rchild = NULL;
        return 1; // 返回1， 插入成功
    } else if(key == T -> data) { // 树中存在相同的关键字，插入失败
        return 0;
    } else if(key < T -> data) { // 插入T的左子树
        return BST_Insert(T -> lchild, key);
    } else { // 插入T的右子树
        return BST_Insert(T -> rchild, key);
    }
}

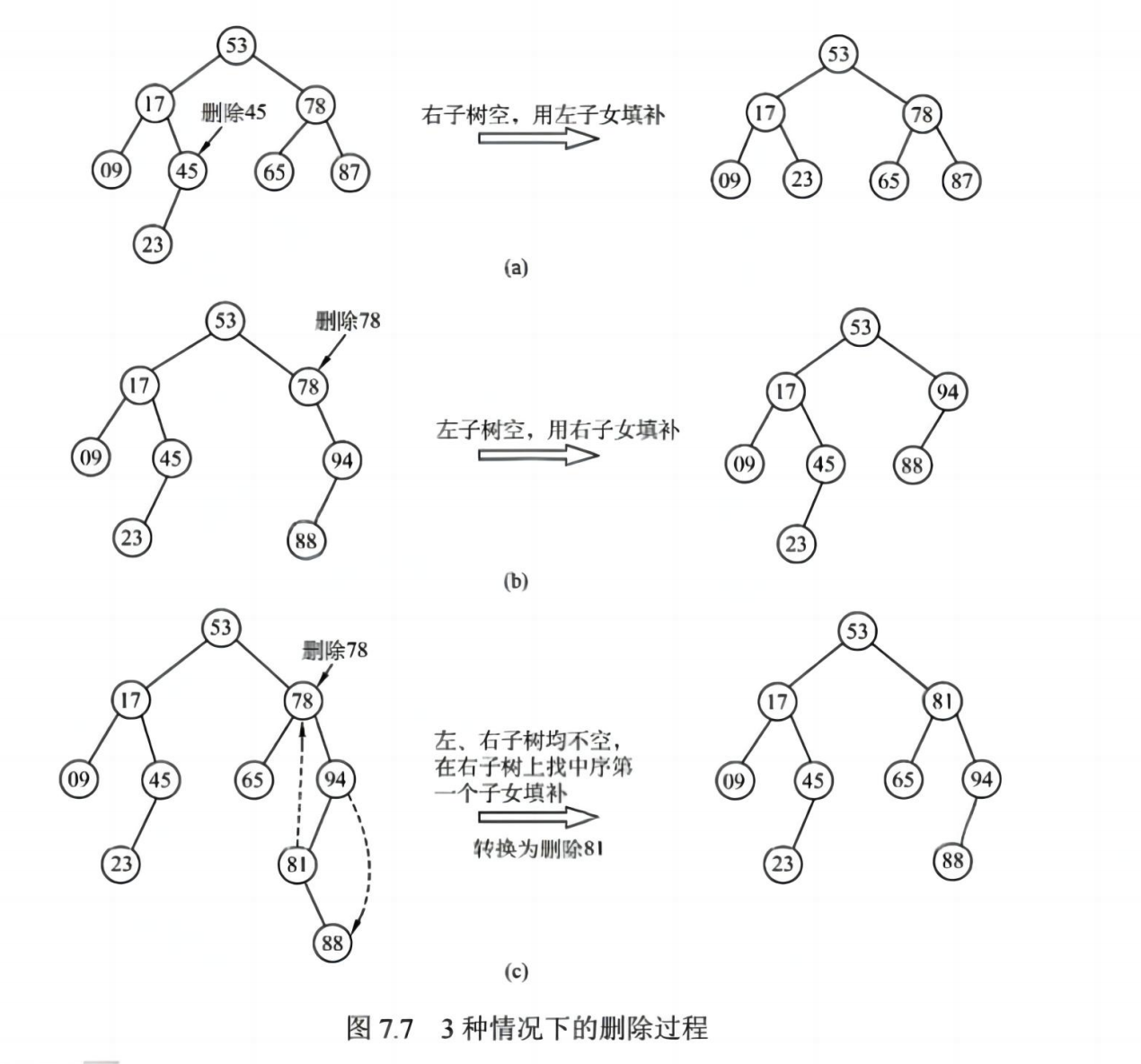
• 删除 ：三种情况
  • 无子树 → 直接删
  • 一个子树 → 替换
  • 两个子树 → 找后继或前驱替换

📌 性质：

• 中序遍历得到有序序列
• 平衡时查找效率高，最坏退化为链表

💡 考点：构造 BST、插入/删除操作、判断是否为 BST

---

✅ （二）平衡二叉树（AVL 树）

📌 定义：

• 是一种自平衡二叉排序树
• 任意节点的左右子树高度差 ≤ 1

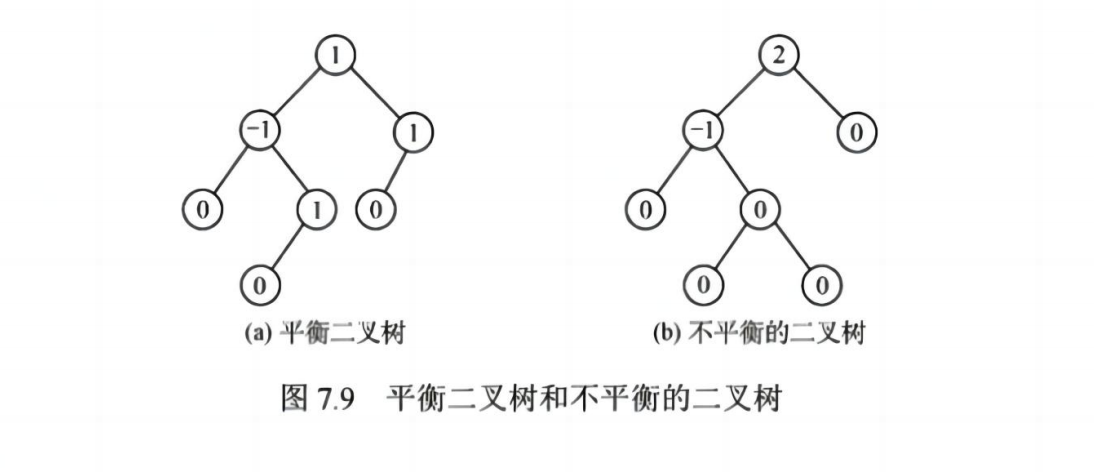
📌 平衡因子（BF）：

• BF=左子树高度−右子树高度BF=左子树高度−右子树高度
• BF ∈ {-1, 0, 1}

📌 失衡处理（四种旋转）：

类型	说明
LL 型	左孩子左子树过高 → 右旋
RR 型	右孩子右子树过高 → 左旋
LR 型	左孩子右子树过高 → 先左旋再右旋
RL 型	右孩子左子树过高 → 先右旋再左旋

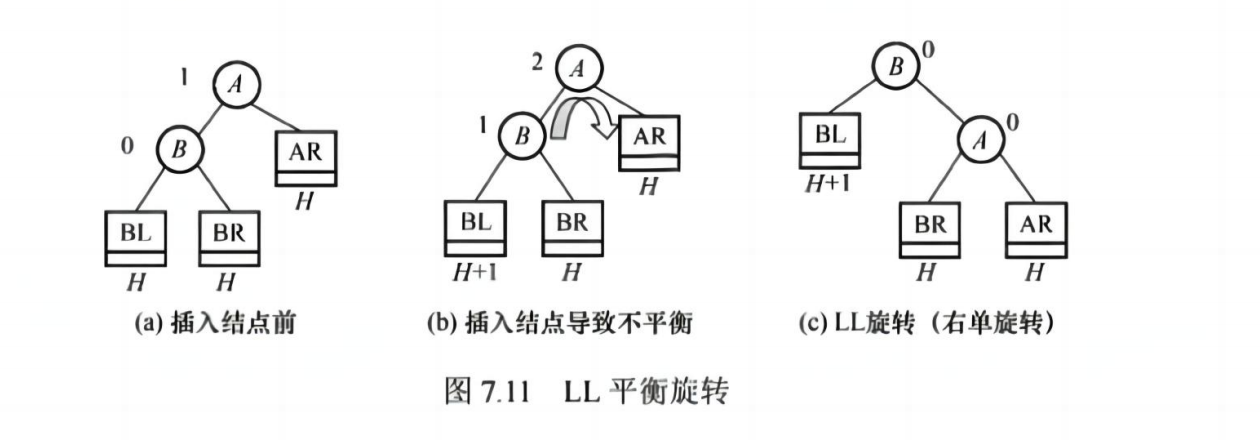
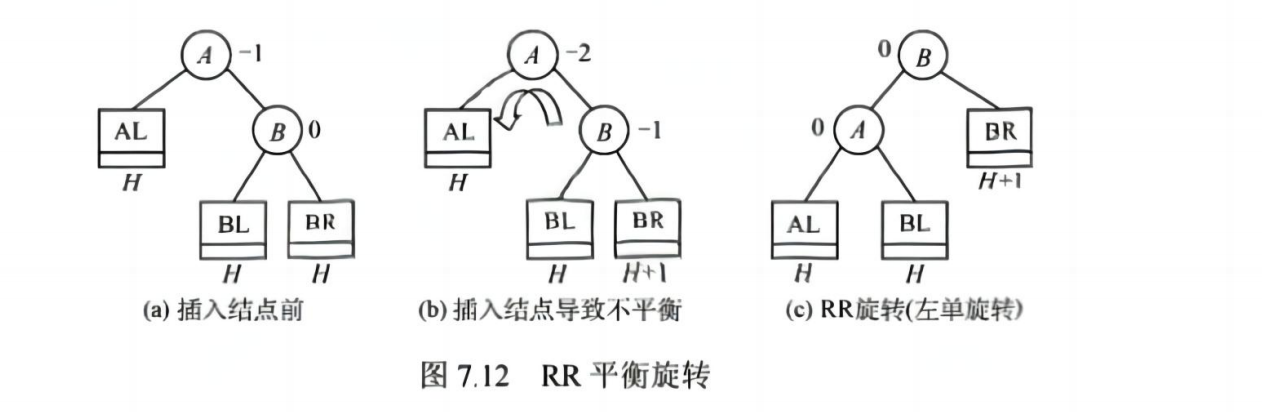
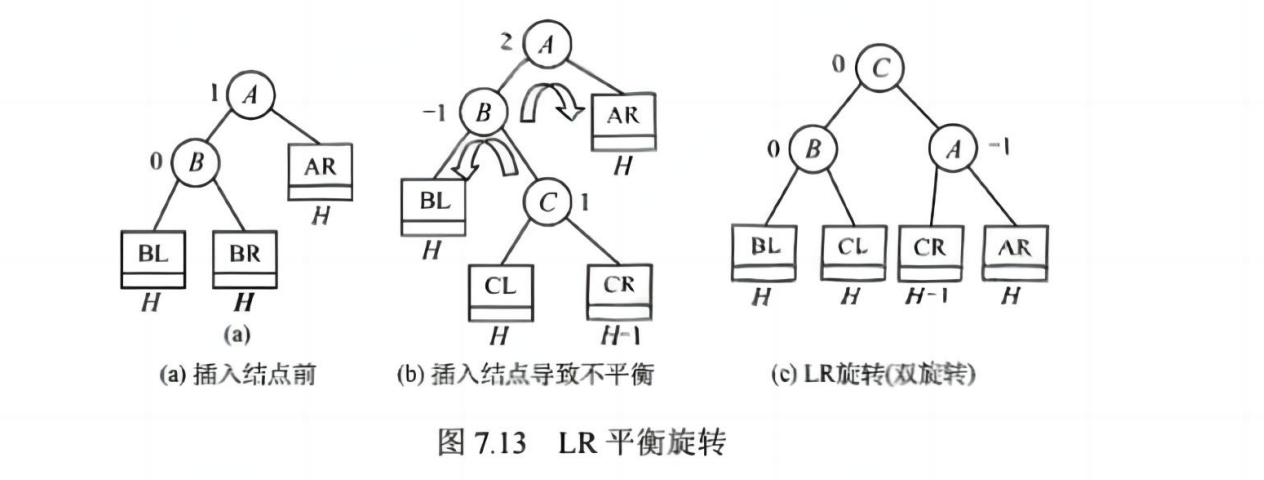
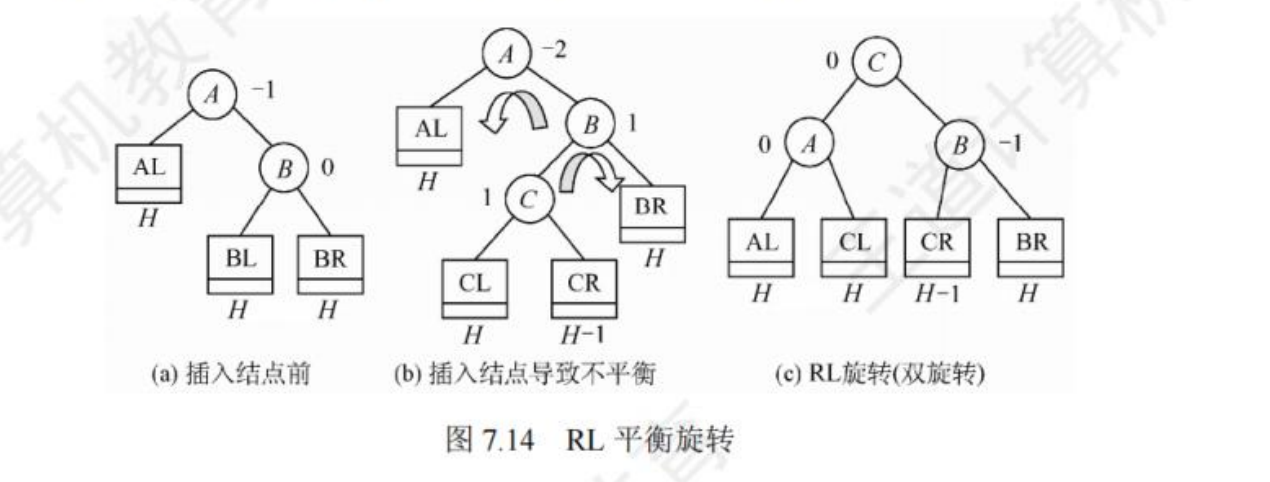
💡 考点：理解旋转机制，能判断失衡类型并画出调整后的树

---

✅ （三）红黑树

📌 定义：

• 是一种近似平衡的二叉排序树
• 保证最长路径不超过最短路径的 2 倍

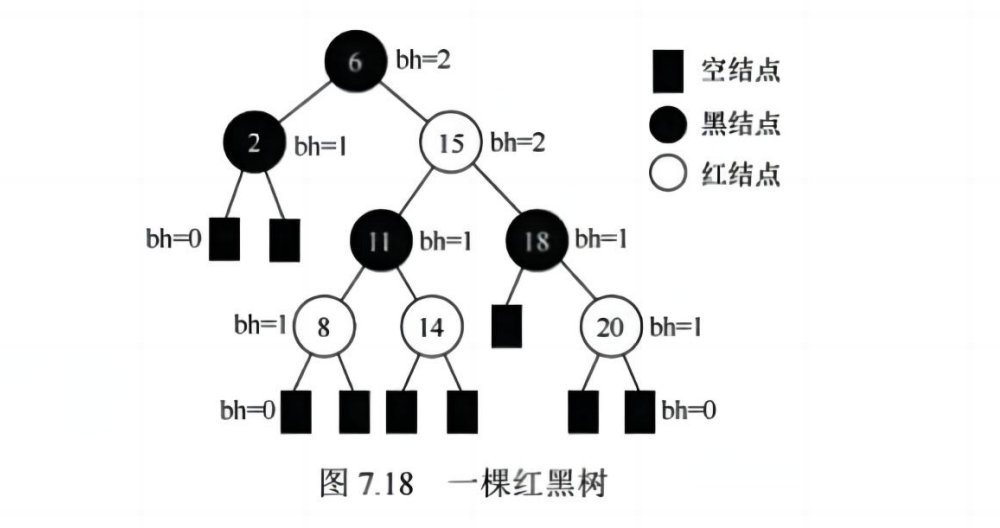
📌 五条性质（必须记住）：

1. 每个节点是红或黑
2. 根是黑色
3. 叶子（NIL）是黑色
4. 红节点的子节点必须是黑
5. 任一节点到其叶子的所有路径包含相同黑节点数

🔥 红黑树的插入规则（核心考点！）

红黑树的插入过程分为两步：

第一步：按 BST 规则插入新节点，并将其染为红色

• 新节点总是作为叶子插入
• 初始颜色设为 红色（避免破坏性质5，因为增加红节点不影响黑高）

第二步：修复可能被破坏的红黑性质

插入红色节点后，唯一可能被破坏的是性质4 （红-红冲突）。

我们通过重新着色 （recoloring）和旋转（rotation）来修复。

⚠️ 注意：根节点始终要保持黑色，若修复后根变红，最后需将其染黑。

---

🧩 插入后的三种主要情况（设当前节点为 z，父节点为 p，叔叔节点为 u）

情况	条件	处理方式
情况1	z 的父节点 p 是黑色	✅ 无需调整！直接结束。
情况2	z 的父节点 p 是红色 ，且叔叔节点 u 也是红色	🔁 重新着色 ： - 将 p 和 u 染黑 - 将爷节点 g 染红 - 令 z = g，继续向上检查
情况3	z 的父节点 p 是红色 ，但叔叔节点 u 是黑色（或 NIL）	🔄 旋转 + 重新着色 ： 根据 z 相对于 p 和 g 的位置，分四种子情况： 1. LL 型 （z 是左孩子，p 是左孩子）→ 右单旋，父换爷+染色 2. RR 型 （z 是右孩子，p 是右孩子）→ 左单旋，父换爷+染色 3. LR 型 （z 是右孩子，p 是左孩子）→ 左右旋，子换爷+染色 4. RL 型 （z 是左孩子，p 是右孩子）→ 右左旋 ****，子换爷+染色

✅ 关键记忆点：

• 先看父
• 父为黑 → 直接插入
• 父为红再看叔
• 叔为红 → 变色上移
• 叔为黑或NULL → 旋转调整

---

📌 优势：

• 插入/删除效率稳定，
• 实际应用广泛（如 Linux 内核、Java TreeMap）

💡 考点：理解红黑树性质，了解其用途，不要求手写旋转

---

✅ （四）B 树与 B+ 树（难点！）

📌 B 树（B-tree）

✅ 定义：

• 多路搜索树，常用于数据库和文件系统
• 所有叶子在同一层，非叶子节点至少有 ⌈m/2⌉ 个子树（除根结点）

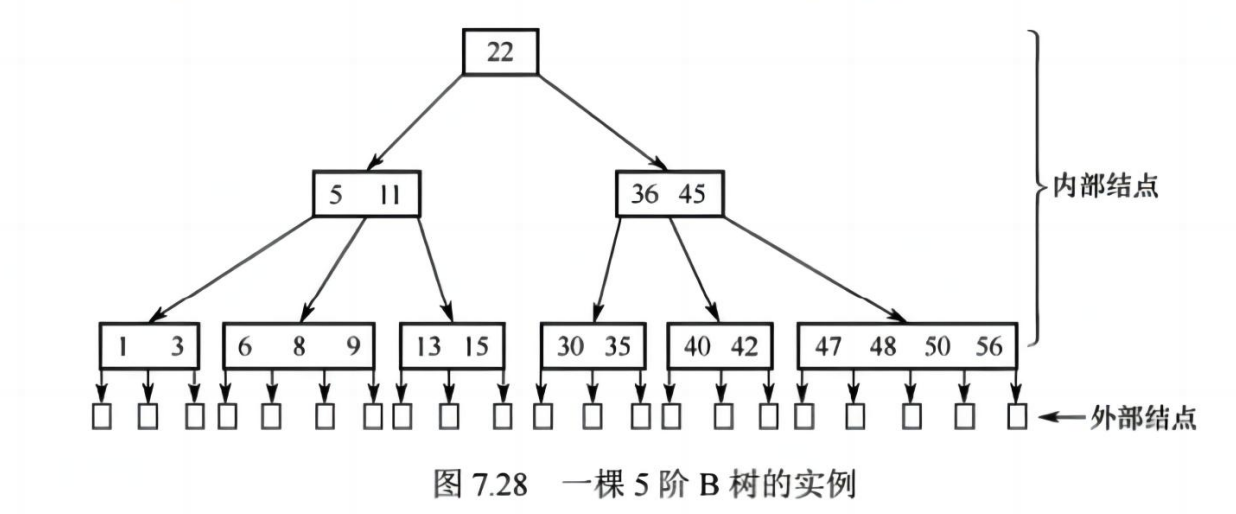
✅ 性质：

• 每个节点最多 m 个子树，m -1 个关键字
• 关键字按顺序排列，子树按大小划分区间
• 插入、删除可能导致分裂或合并

✅ 操作：

• 查找：从根开始，按区间递归
• 插入：先查找，若满则分裂

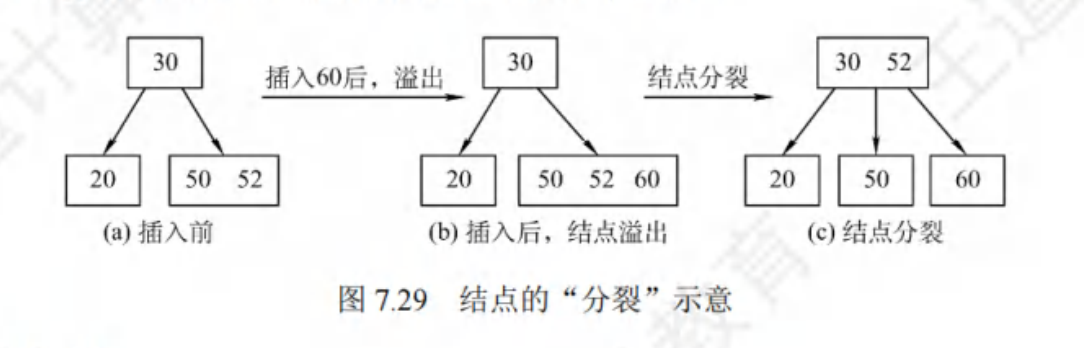
• 删除：若不足则借或合并

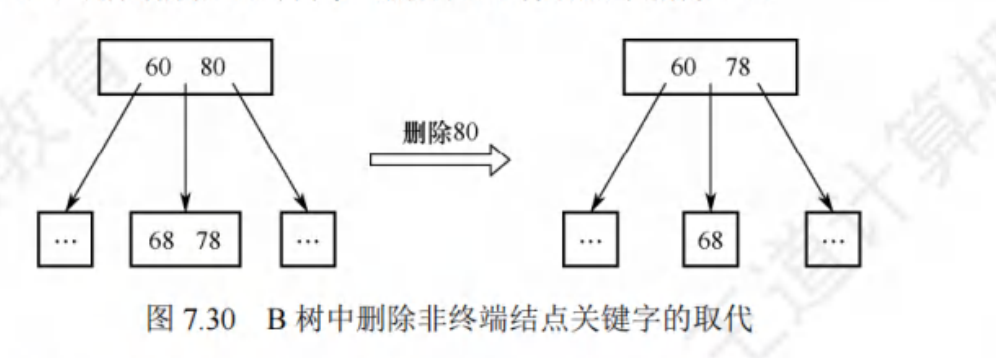
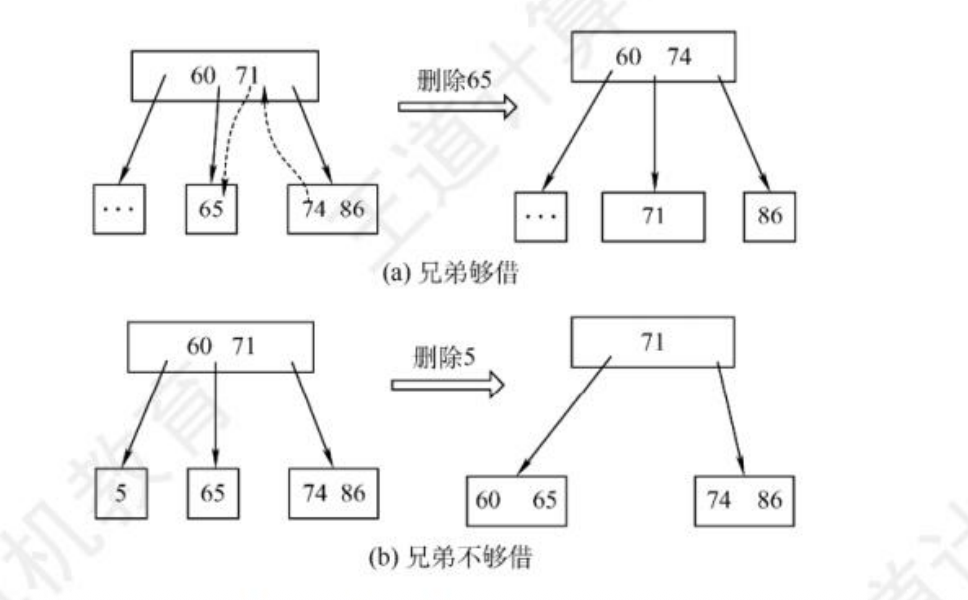
💡 考点：掌握插入、删除、查找的操作过程（王道要求）

📌 B+ 树（B+-tree）

✅ 与 B 树的区别：

对比项	B 树	B+ 树
数据存储位置	所有节点（包括非叶子）都可存数据	仅叶子节点存数据，非叶子只存索引
关键字重复	每个关键字在整个树中唯一	关键字在非叶子（索引）和叶子（数据）中重复出现
叶子节点结构	无连接	所有叶子通过指针链接成链表
范围查询效率	低（需多次回溯）	高（顺序遍历叶子即可）
典型应用	较少用于现代数据库	MySQL、Oracle 等数据库索引

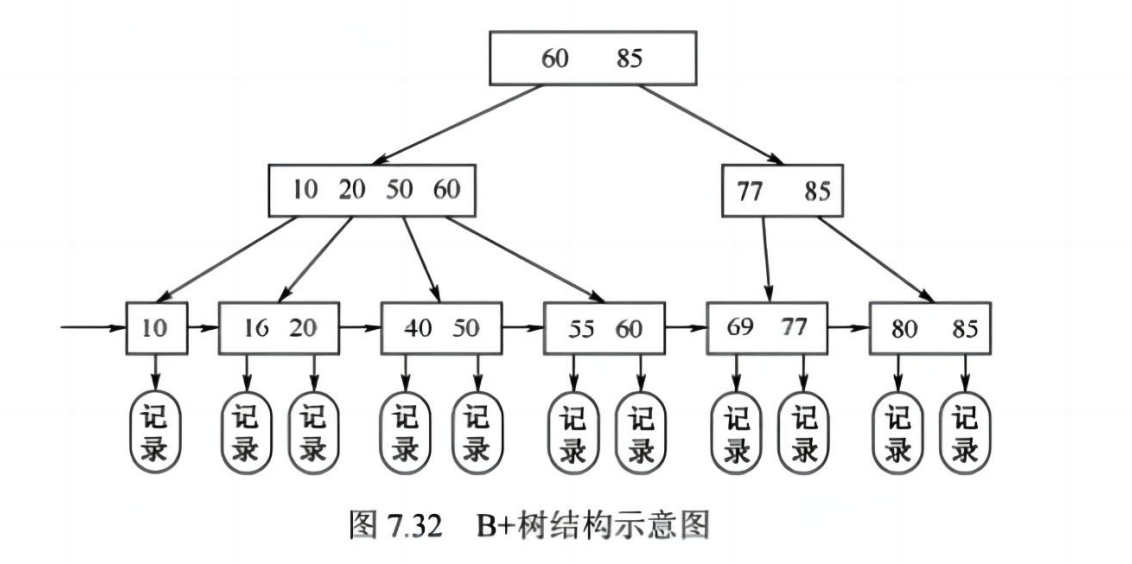
✅ 优点：

• 更适合磁盘存储（减少 I/O）
• 支持高效范围查询（如 SELECT * FROM table WHERE id > 10）

💡 考点：了解基本概念和性质，知道用于数据库索引

---

四、散列（Hash）表（重点！）

✅ 基本思想：

• 通过散列函数将关键字映射到地址，实现快速查找

✅ 散列函数设计原则：

• 均匀分布
• 计算简单
• 减少冲突

✅ 常见散列函数：

• 直接定址法
• 除留余数法（最常用）
• 平方取中法
• 折叠法

✅ 冲突处理方法（必须掌握）：

方法	原理	优点	缺点
开放定址法	在表内寻找空闲位置	不需额外空间	聚集问题严重
拉链法	每个桶挂一个链表	无聚集，易扩展	需额外指针空间
公共溢出区	单独区域存放冲突元素	便于管理	需额外空间

💡 考点：理解各种方法的原理，能画出链地址法的结构图

✅ 散列查找的性能分析

散列表的查找效率主要取决于三个因素

• 散列函数
• 冲突处理方法
• 装填因子（α）

装填因子 α = 表中元素个数 n / 散列表长度 m

ASL= 查找长度 / 地址数（地址数是用作%的数，不是表长！！！）

✅ 散列表 ASL 计算（线性探测法）

关键字 ：22, 41, 53, 46, 30, 13
H(key) = key % 11，表长 m = 11

最终散列表：

地址	0	1	2	3	4	5	6	7	8	9	10
关键字	22		46	13					41	53	30

• ASL成功 = (1+1+1+1+3+2)/6 = 1.5
• ASL失败 = (2+1+3+2+1+1+1+1+5+4+3)/11 = 24/11 ≈ 2.18

注：失败查找从每个地址 i 开始，循环探测至第一个"真正空"单元（地址1、4～7）。

---

⚠️ 重要注意事项（开放定址法）

• 删除元素时不能置空，需设为"已删除"标记（tombstone）。
• 查找时遇到"已删除"单元必须继续探测 ，只有遇到从未使用的空槽才停止。
• 因此，ASL失败 的终止条件是"真正空"，不是"已删除"。

考研若未提删除，默认无标记，按上述方法计算即可。
💡 考点：计算 ASL，分析性能

---