文章目录
前言
1、什么是搜索? 搜索,本质是一种枚举,通过穷举所有的情况来找到最优解,或者统计合法解的个数。因此,搜索有时候也叫作暴搜。
搜索一般分为深度优先搜索 (DFS) 与宽度优先搜索 (BFS)。 深度优先遍历 vs 深度优先搜索,宽度优先遍历 vs 宽度优先搜索
遍历是形式,搜索是目的。 不过,在一般情况下,我们不会去纠结概念的差异,两者可以等同。
2、回溯与剪枝回溯:当在搜索的过程中,遇到走不通或者走到底的情况时,就回头。
剪枝:剪掉在搜索过程中,剪掉重复出现或者不是最优解的分支。
3、搜索题目解题策略
- 画决策树;
- 根据决策树写递归。
下面以输出1-3的全排列为列来让大家理解什么是决策树:
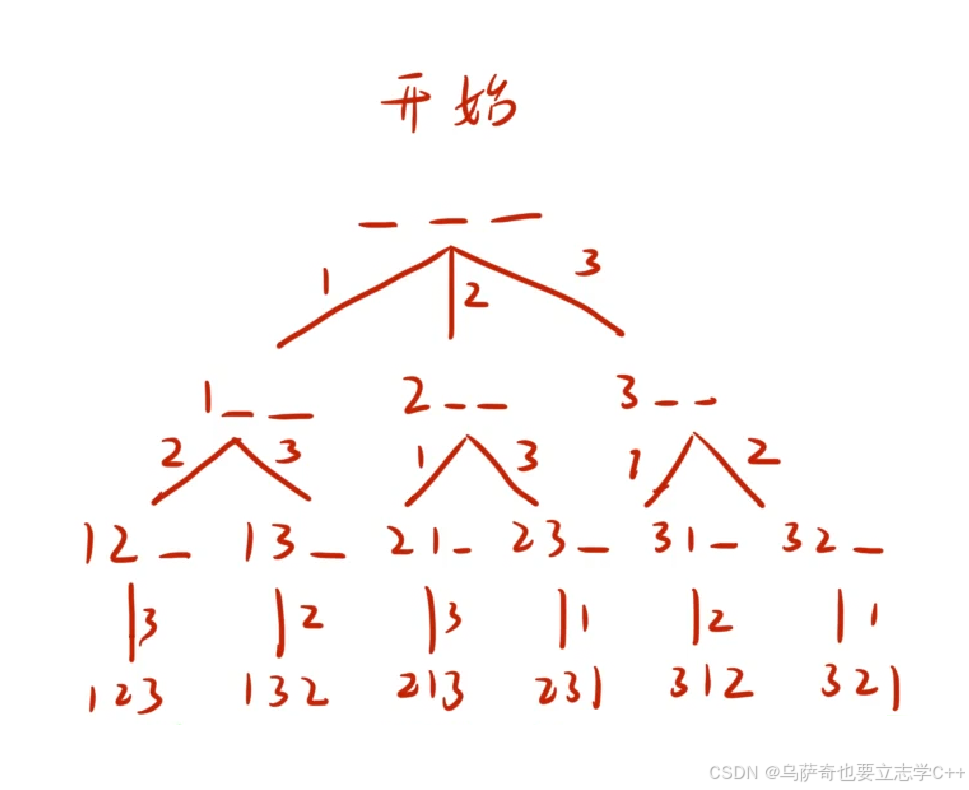
上图就是一颗决策树,每一层选1、选2还是选3其实就是策略,决策树其实就是我们在初高中时学习的树状图。
枚举子集
题目描述
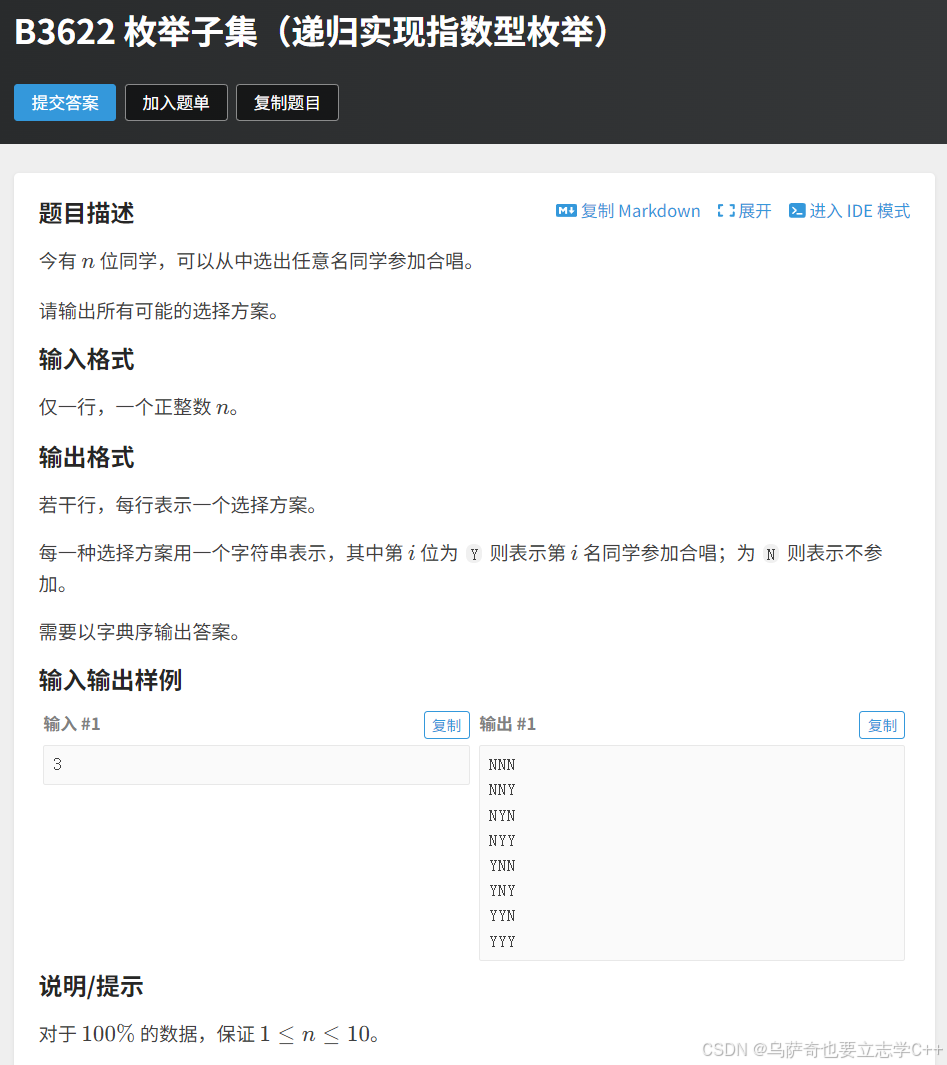
题目解析
解决搜索题目我们要先画出决策树,因为本题要按字典序排序,字符Y的字典序比N大,所以我们要先选择N,再选择Y,决策树如下图所示:
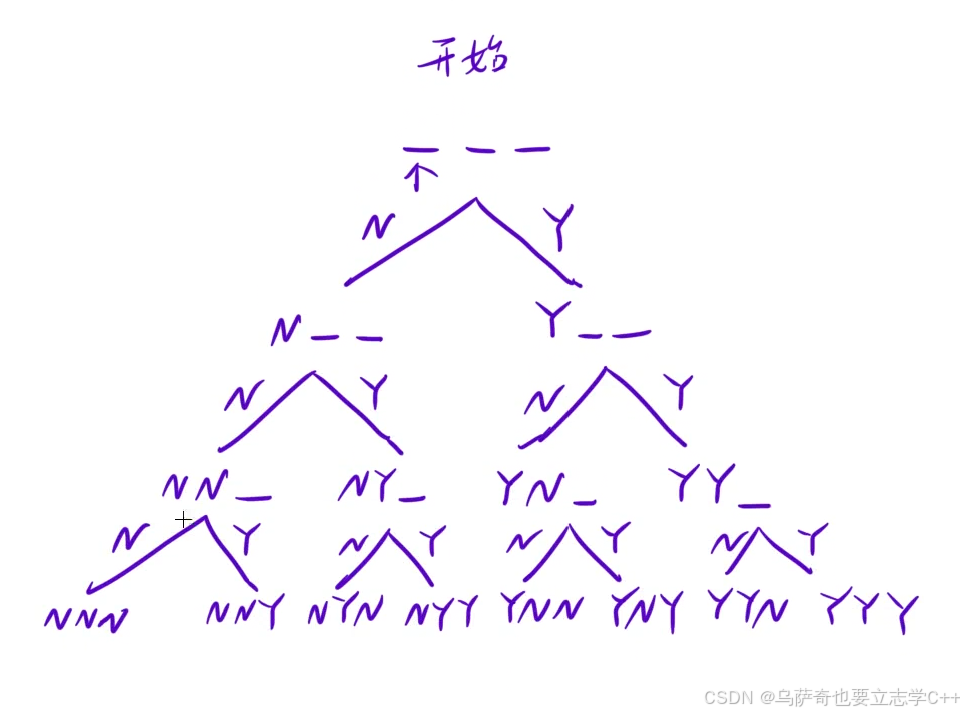
下面我们就要根据决策树写递归代码了,写这类代码策略是善用全局变量和回溯 ,因为本题需要输出字符串,所以就可以用一个全局字符串来记录每一步的递归搜索结果,其他题如果输入的数据是数组就可以用一个全局数组来存储搜索结果。 在递归代码中参数pos代表当前选择字符串从左到右第几个位置,我们先写不选择情况,path += "N",再写选择情况,path += "Y",然后继续递归下一个位置dfs(pos+1),注意递归返回后要把刚才在当前递归函数栈帧中往全局字符串中加入的字符pop掉,这一步非常重要,叫做回溯,恢复现场。
代码
问题:叶子结点递归两次不会输出两次结果吗?
不会,叶子结点不会递归两次,递归到叶子结点输出结果后就直接返回了。
cpp
#include <iostream>
#include <string>
using namespace std;
int n;
string path;
void dfs(int pos)
{
if (pos > n)
{
cout << path << endl;
return;
}
//不选
path += "N";
dfs(pos + 1);
path.pop_back(); //回溯,恢复现场
//选
path += "Y";
dfs(pos + 1);
path.pop_back(); //回溯,恢复现场
}
int main()
{
cin >> n;
dfs(1);
return 0;
}组合型枚举
题目描述
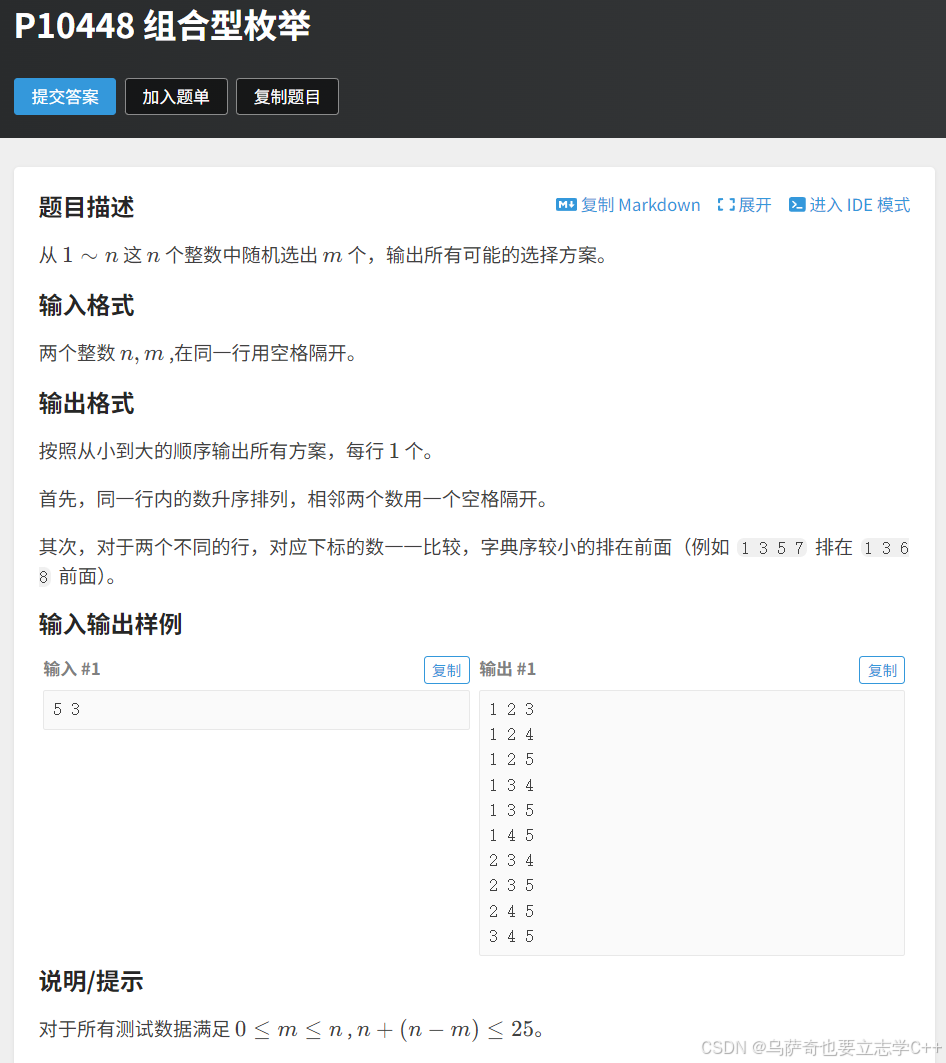
题目解析
本题还是运用搜索代码实现方法,先画决策树:
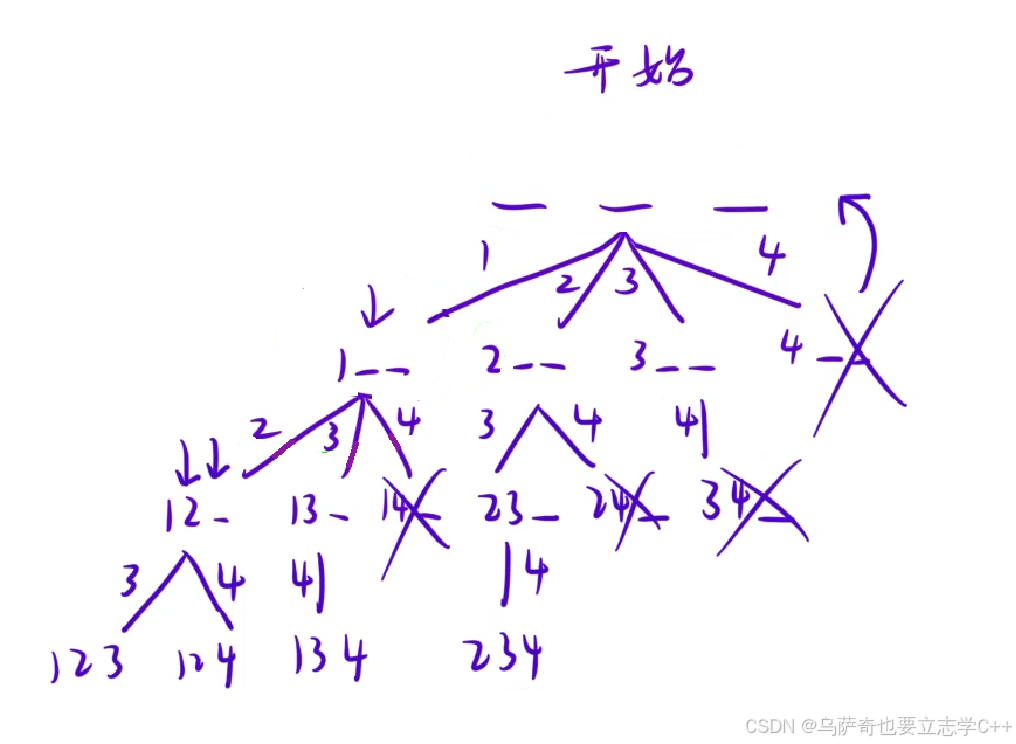
然后根据决策树写代码,小编要补充一点,在递归函数中没有额外判断数选不够需要直接回溯的情况:14_、34_等,因为当递归到上述情况时会因为不满足for循环继续dfs的条件,跳过for循环从而正常跳过函数调用结束返回,所以不需要额外判断。
代码
cpp
#include <iostream>
#include <vector>
using namespace std;
int n, m;
vector<int> a;
//pos表示填哪个位置,begin表示从哪个数开始填
void dfs(int pos, int begin)
{
if (pos > m)
{
for (auto& e : a)
{
cout << e << " ";
}
cout << endl;
return;
}
for (int i = begin; i <= n; i++)
{
a.push_back(i);
dfs(pos + 1, i + 1);
a.pop_back();
}
}
int main()
{
cin >> n >> m;
dfs(1, 1);
return 0;
}枚举排列
题目描述
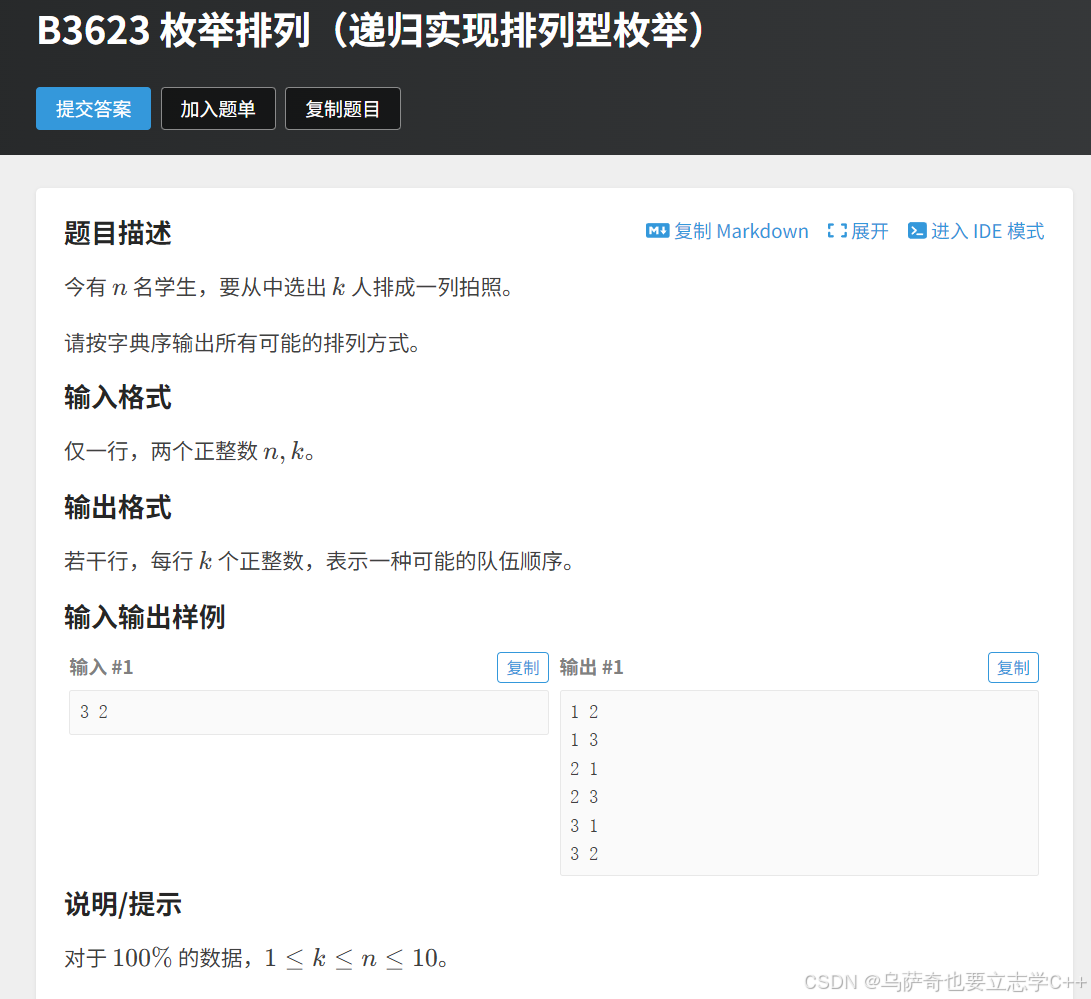
题目解析
依旧先画决策树:
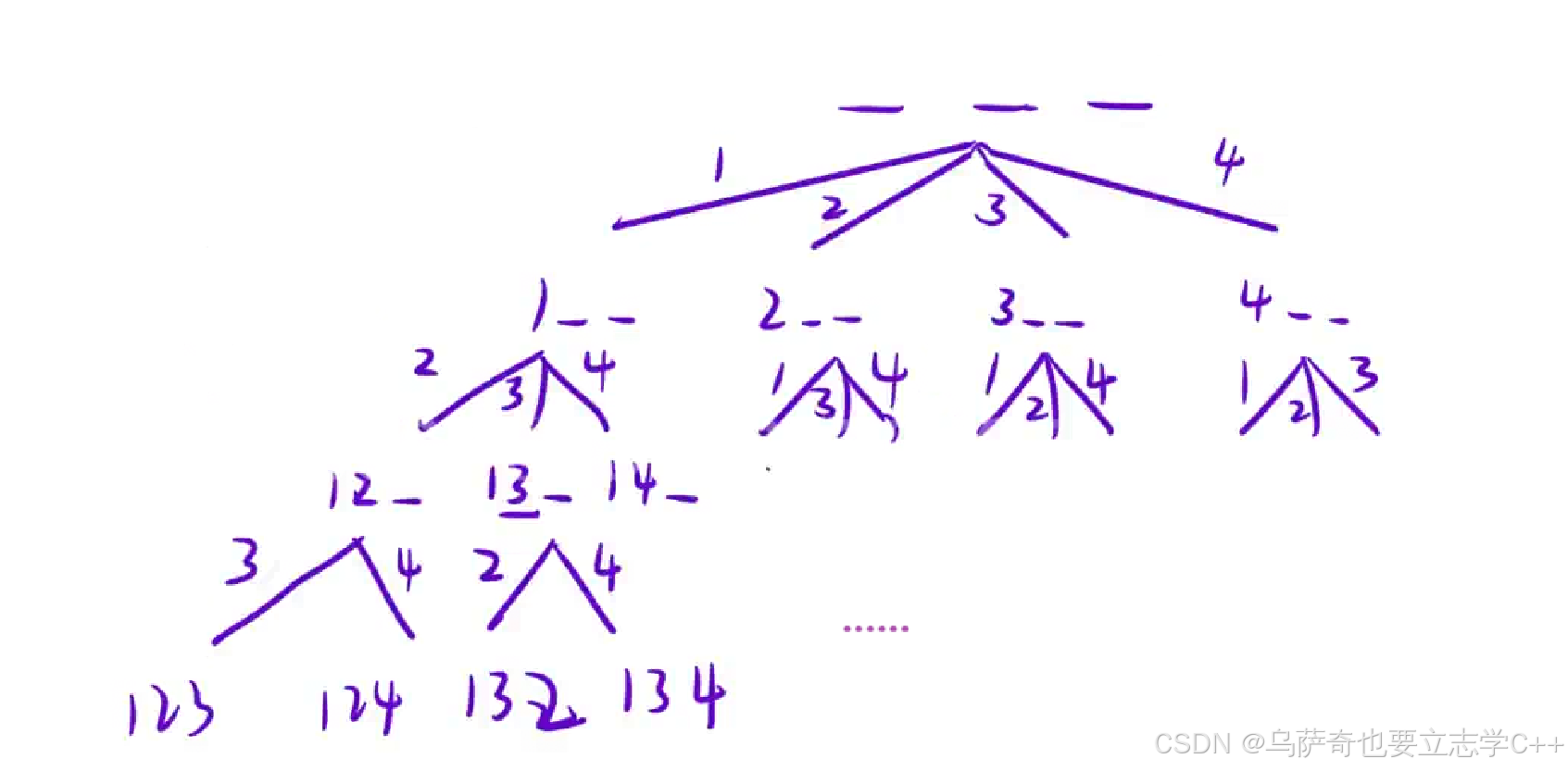
本题和上一题的区别是不用排升序,所以需要额外添加一个数组st标记选择了哪些数,并且在恢复现场也需要恢复st数组。
代码
cpp
#include <iostream>
#include <vector>
using namespace std;
const int N = 15;
int n, k;
vector<int> a; //存储每一次选数情况
bool st[N]; //标记有哪些数已经被选过了
void dfs(int pos)
{
if (pos > k)
{
for (auto& e : a)
{
cout << e << " ";
}
cout << endl;
return;
}
for (int j = 1; j <= n; j++)
{
//枚举所有在pos位置可能出现的数
if (st[j])
{
//j已被选,直接continue
continue;
}
st[j] = true;
a.push_back(j);
dfs(pos + 1);
//恢复现场
a.pop_back();
st[j] = false;
}
}
int main()
{
cin >> n >> k;
dfs(1);
return 0;
}全排列问题
题目描述
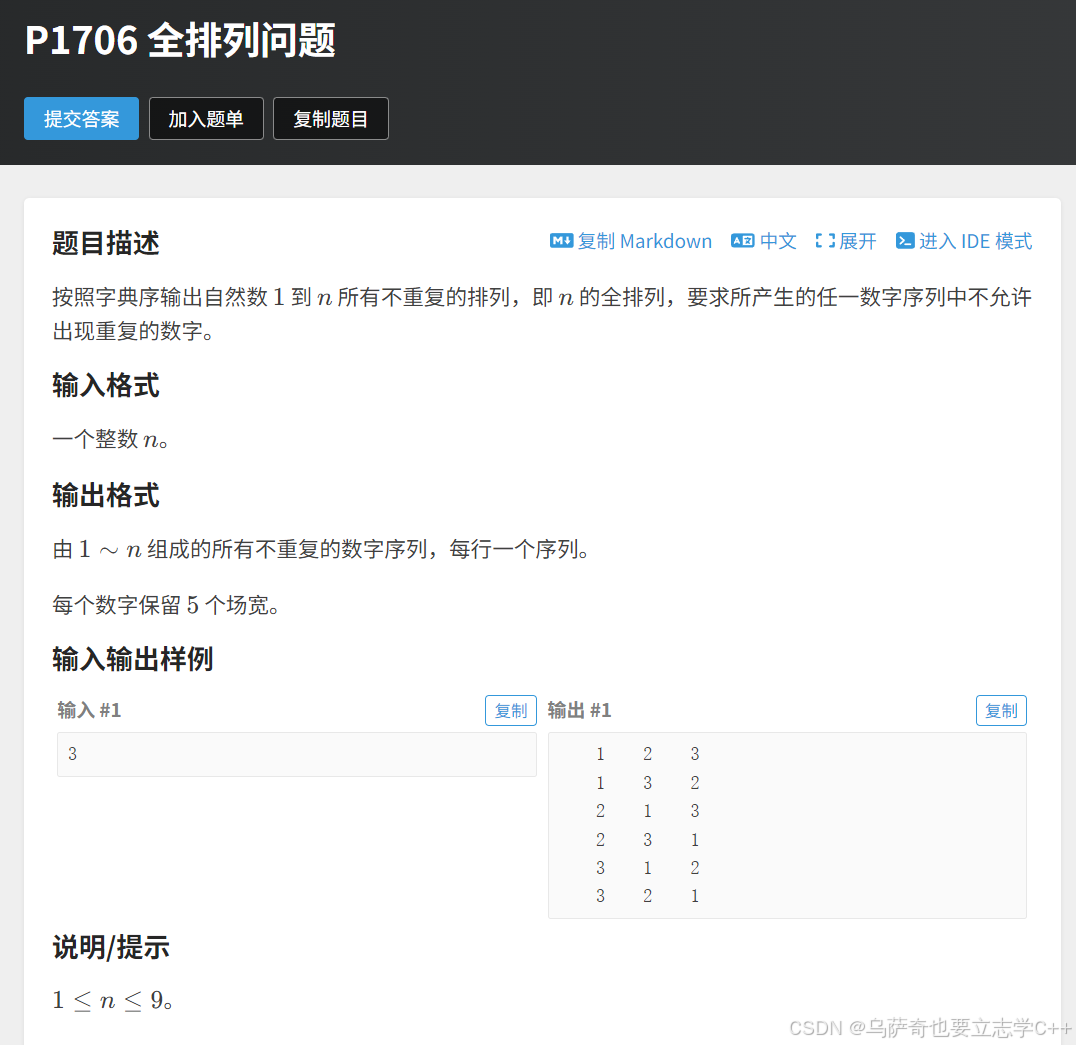
题目解析
本题思路基本和上一题一样,唯一需要注意的是题目要求输出保留5个场宽。
代码
cpp
#include <iostream>
#include <vector>
using namespace std;
const int N = 15;
int n;
vector<int> a;
int st[N];
void dfs(int pos)
{
if (pos > n)
{
for (auto& e : a)
{
printf("%5d", e);
}
cout << endl;
return;
}
for (int i = 1; i <= n; i++)
{
if (st[i])
continue;
st[i] = true;
a.push_back(i);
dfs(pos + 1);
a.pop_back();
st[i] = false;
}
}
int main()
{
cin >> n;
dfs(1);
return 0;
}总结
DFS 回溯的「万能核心公式」(这是所有回溯题的通用逻辑)
所有 DFS 回溯类题目,递归函数的核心逻辑都是 三步闭环,无一例外:
① 做出选择(比如:path 加字符、a 加数字、st 标记选中)
② 递归深搜(进入下一层决策:dfs (pos+1))
③ 撤销选择 / 恢复现场(回溯核心:path.pop_back ()、a.pop_back ()、st [j]=false)
以上就是小编分享的全部内容了,如果觉得不错还请留下免费的赞和收藏
如果有建议欢迎通过评论区或私信留言,感谢您的大力支持。
一键三连好运连连哦~~
