1.官方文档的检索方式

我们已经掌握了相当多的机器学习和python基础知识，现在面对一个全新的官方库，看看是否可以借助官方文档的写法了解其如何使用。

我们以pdpbox这个机器学习解释性库来介绍如何使用官方文档。

大多数 Python 库都会有官方文档，里面包含了函数的详细说明、用法示例以及版本兼容性信息。

通常查询方式包含以下2种：

GitHub 仓库：
PyPI 页面：
官方文档：

一般通过github仓库都可以找到对应的官方文档那个。

-在官方文档中搜索函数名，然后查看函数的详细说明和用法示例

2.官方文档的阅读和使用

在官方文档中，通常会有一个"API Reference"或"Documentation"部分，列出所有可用的函数、类和方法。

pdpbox这个库比较小，所以非常适合我们学习用法。

以pdpbox库中的info_plots模块下的TargetPlot类为例，

先导入这个类（三种不同的导入和引用方法）
传入实例化参数

上述图片包含了实例化参数和实例化后具备的属性和方法。

复制代码

# 首先要确保库的版本是最新的，因为我们看的是最新的文档，库的版本可以在github上查看
import  pdpbox
print(pdpbox.__version__)  # pdpbox版本
# 导入这个类
from pdpbox.info_plots import TargetPlot  # 导入TargetPlot类

可以鼠标悬停在这个类上，来查看定义这个类所需要的参数，以及每个参数的格式

ctrl进入可以查看这个类的详细信息

只能查看到他的初始化方法，但是无法看到他的普通方法。注意到提示我们有plot方法，但是看不到普通方法需要传入的参数

可以发现这个类继承了_InfoPlot类，此时我们再次进入_InfoPlot类里面，可以找到这个继承的plot方法

复制代码

# 选择待分析的特征（如：petal length (cm)）
feature = 'petal length (cm)'
feature_name = feature  # 特征显示名称

# 初始化TargetPlot对象（移除plot_type参数）
target_plot = TargetPlot(
    df=df,  # 原始数据（需包含特征和目标列）
    feature=feature,  # 目标特征列
    feature_name=feature_name,  # 特征名称（用于绘图标签）
    # target='target',  # 多分类目标索引（鸢尾花3个类别）
    target='target',  # 多分类目标索引（鸢尾花3个类别）
    grid_type='percentile',  # 分桶方式：百分位
    num_grid_points=10  # 划分为10个桶

# 调用plot方法绘制图形
target_plot.plot()
# 看起来很奇怪，我们查看下类型
type(target_plot.plot())
len(target_plot.plot()) # 查看元组的形状，元组只有len方法，没有shape方法

依次查看这个元组返回的究竟是什么内容？

target_plot.plot()[0] #图片

target_plot.plot()[1]

居然什么也没有返回

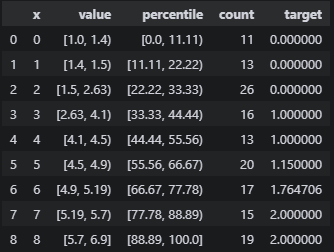
这个返回的是目标变量（或预测值）在不同特征区间的统计摘要。这是 PDPbox（Partial Dependence Plot）库生成的核心分析数据。他已经在图上被可视化出来了

target_plot.plot() 返回的是一个三元组（tuple），包含：

Figure 对象 ：matplotlib.figure.Figure 或 plotly.graph_objects.Figure（看你用哪个引擎）

Axes 字典 ：dict[str, matplotlib.axes.Axes]，如果用的是 plotly 引擎则为 None

summary_df ：一个 pd.DataFrame，里面是"每个分桶的统计汇总"（比如各桶的样本量、各类别/目标的聚合统计等）

在官方文档介绍中的plot方法最下面，写明了参数和对应的返回值

综上需要注意，我们关注一个类需要关注如下信息

传入的参数和对应的格式
类对应的方法的返回值

最后，我们用规范的形式来完成

复制代码

fig, axes, summary_df = target_plot.plot(
    which_classes=None,  # 绘制所有类别（0,1,2）
    show_percentile=True,  # 显示百分位线
    engine='plotly',
    template='plotly_white'
)

# 手动设置图表尺寸（单位：像素）
fig.update_layout(
    width=800,  # 宽度800像素
    height=500,  # 高度500像素
    title=dict(text=f'Target Plot: {feature_name}', x=0.5)  # 居中标题
)

fig.show()

其中，fig.update_layout() 是对 Plotly 图表进行二次修改的核心方法。很多绘图工具都是调用的底层的绘图包，所以要想绘制出想要的图表，需要先了解底层绘图包的语法。

作业：

复制代码

from pdpbox.info_plots import InteractTargetPlot

feature_1 = 'petal length (cm)'
feature_2 = 'petal width (cm)'

interact_target_plot = InteractTargetPlot(
    df=df,
    features=[feature_1, feature_2],
    feature_names=[feature_1, feature_2],
    target='target',
    grid_types=['percentile', 'percentile'],  # <- 注意这里是复数 + 列表
    num_grid_points=[10, 10]
)

fig, axes, summary_df = interact_target_plot.plot(
    which_classes=None,
    show_percentile=True,
    engine='plotly',
    template='plotly_white'
)

fig.update_layout(
    width=900,
    height=650,
    title=dict(text='InteractTargetPlot: petal length × petal width', x=0.5)
)
fig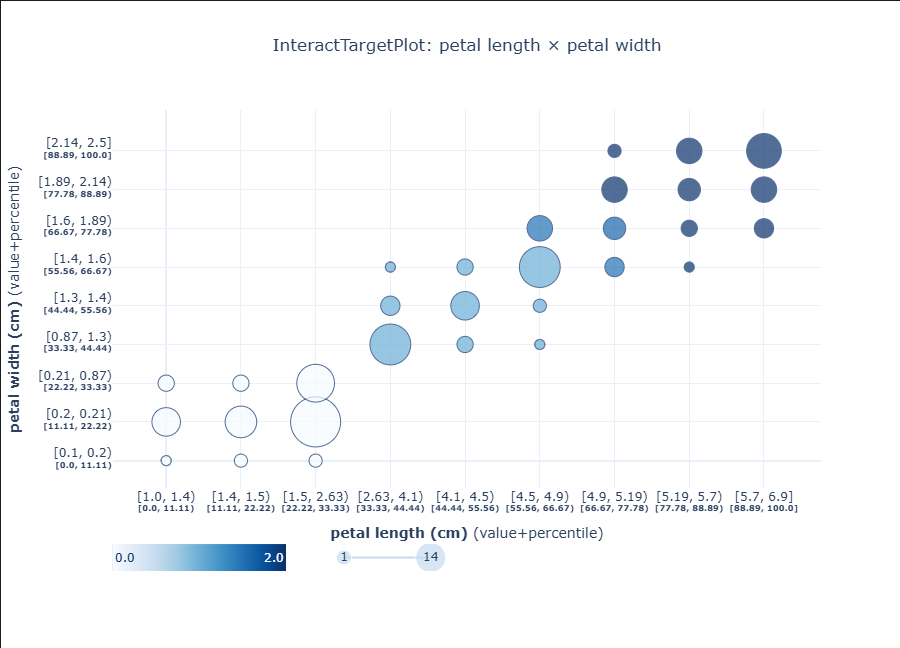

复制代码

from pdpbox.info_plots import InteractPredictPlot

# 选两个特征
f1 = 'petal length (cm)'
f2 = 'petal width (cm)'

def pred_func(model, X):
    return model.predict_proba(X)  # shape: (n_samples, 3)


ip = InteractPredictPlot(
    df=df,
    features=[f1, f2],
    feature_names=[f1, f2],
    model=model,
    model_features=features,
    pred_func=pred_func,
    n_classes=3,
    grid_types=['percentile', 'percentile'],
    num_grid_points=[10, 10]
)

fig, axes, summary_df = ip.plot(
    which_classes=[2],          # 只画第2类（virginica），避免图太乱
    show_percentile=True,
    engine='plotly',
    template='plotly_white'
)

fig.update_layout(width=900, height=650,
                  title=dict(text='InteractPredictPlot: P(class=2) vs petal length × petal width', x=0.5))
fig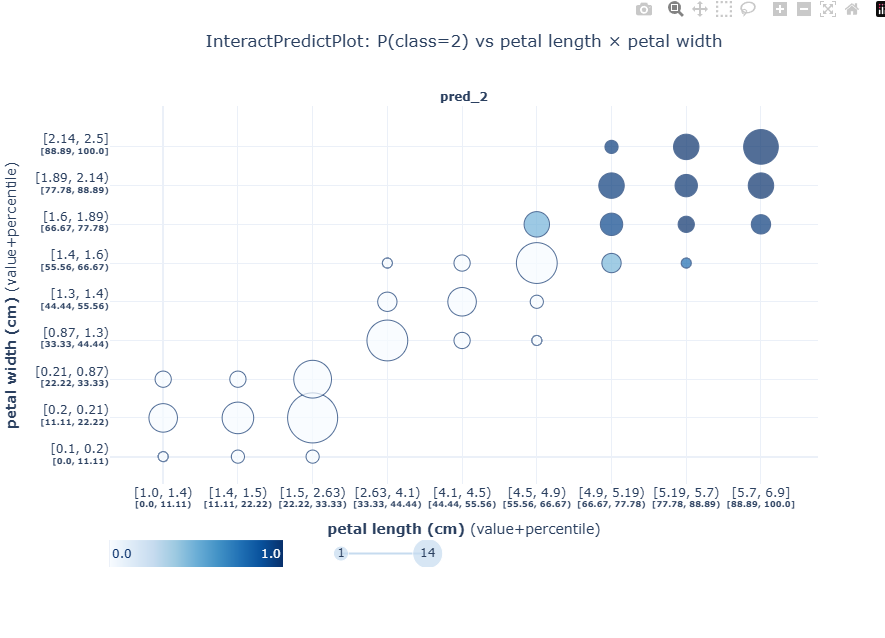

几个疑问：

既然都是预测y的分布，为什么InteractPredictPlot需要指定标签，InteractTargetPlot就不需要?

InteractTargetPlot 的目标是单列 y（天然包含所有类）；InteractPredictPlot 的预测在分类里是多列概率（你得告诉它要画哪一列/哪些列）。

InteractPredictPlot 背后做的事情:

以某个样本的预测概率是 [0.05, 0.90, 0.05] 为例，你选的是 class=2 （pred_2），所以对这个样本取的就是 0.05。

然后对每个样本都会做：

看它的两个特征值
- petal length = 某个数
- petal width = 某个数
根据分桶规则（percentile）把它"归到某个格子/桶"里

比如落到：
- x 方向第 i 个区间
- y 方向第 j 个区间
  
  → 就是二维网格里的一个格子
把这个样本的 "P(class=2)"（这里是 0.05）记到这个格子里
这个格子里会聚集很多样本的 P(class=2) 值

于是它会计算一个汇总统计（通常是 平均值 mean，有些版本还会带分位数等）
画图时：
- 颜色映射这个格子的汇总值（比如 mean 概率）
- 圆的大小 映射这个格子的样本数（count）
- 悬停框里就显示：count 和 pred_2 的汇总值（你看到的 0.000/接近 0）

DAY32 官方文档的阅读

1.官方文档的检索方式

2.官方文档的阅读和使用

居然什么也没有返回