目录
[十三、Sigmoid 函数](#十三、Sigmoid 函数)
[十七、多分类 Softmax](#十七、多分类 Softmax)
一、回归问题
我们先通过一个具体例子来理解回归问题。
-
数据：工资和年龄（两个特征）
-
目标：预测银行会贷款给我多少钱（标签）
样本数据如下：
| 工资 | 年龄 | 额度 |
|---|---|---|
| 4000 | 25 | 20000 |
| 8000 | 30 | 70000 |
| 5000 | 28 | 35000 |
| 7500 | 33 | 50000 |
| 12000 | 40 | 85000 |
问题是：
工资和年龄都会影响最终银行贷款的结果，那么它们各自有多大的影响？
这里的"影响大小"，就是我们要学习的参数。
二、线性回归的通俗解释
-
-
,
-
-
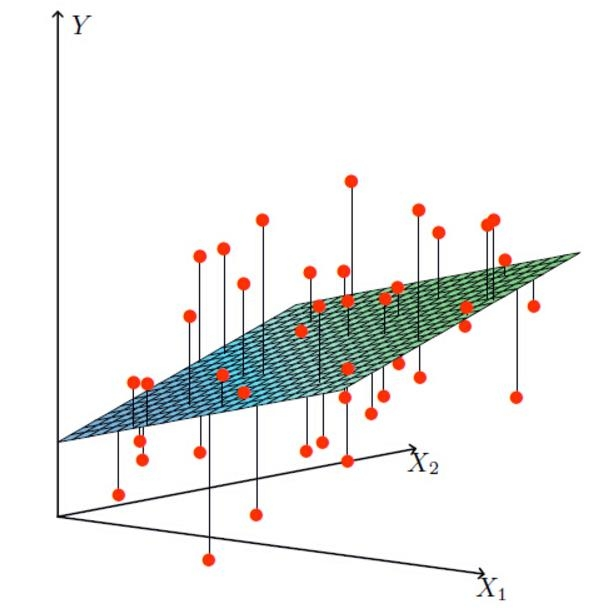
线性回归要做的事情是：
在高维空间中，找到一条（或一个平面），
使其尽可能好地拟合所有数据点。
三、线性回归的数学形式
假设：
-
-
-
拟合的平面表示为：
将其写成统一形式：
四、误差的引入
真实值和预测值之间一定存在差异，这个差异称为误差。
对于每一个样本：
其中：
五、误差的分布假设
我们对误差作如下假设：
-
独立性
不同样本之间的误差相互独立
-
同分布
所有样本的误差来自同一个分布
-
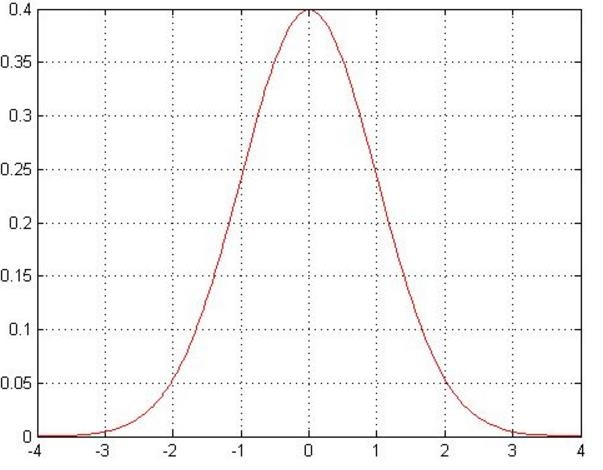
高斯分布
这表示误差均值为 0，方差为 。
六、由误差到条件概率
由预测模型：
又因为误差服从高斯分布：
代入得到条件概率：
七、似然函数与对数似然
假设样本之间相互独立，则总体似然函数为：
取对数得到对数似然：
这样可以把复杂的乘法转化为加法，便于计算。
八、化简得到最小二乘
展开并去掉与参数无关的常数项后，目标变为：
这就是最小二乘法的目标函数。
九、解析解（正规方程）
对目标函数求导并令导数为 0，可以得到闭式解：
十、线性回归的评估方法
常用评估指标是：
十一、梯度下降的引入
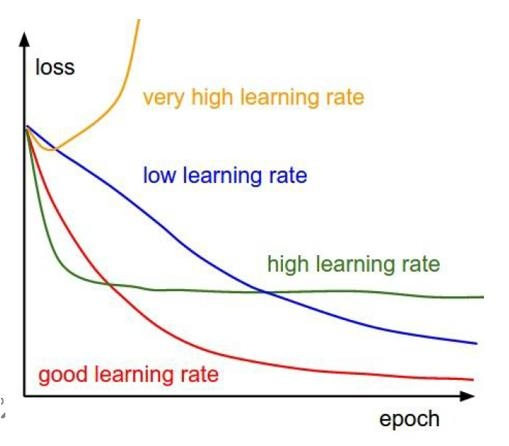
当目标函数难以直接求解时，采用梯度下降法。
核心思想是：
一步一步沿着目标函数下降最快的方向更新参数。
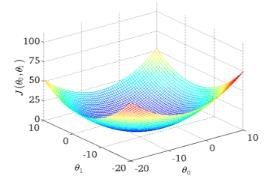
目标函数示例：
梯度下降的三种形式
- 批量梯度下降
- 随机梯度下降
- 小批量梯度下降
十二、逻辑回归
逻辑回归是一个经典的二分类算法。
-
先用逻辑回归
-
再用更复杂的模型
-
能简单就不用复杂
十三、Sigmoid 函数
Sigmoid 函数定义为：
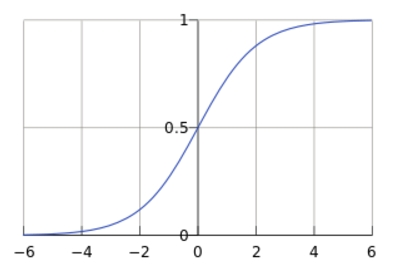
其作用是：
将任意实数映射到区间 0,10,10,1。
十四、逻辑回归的预测函数
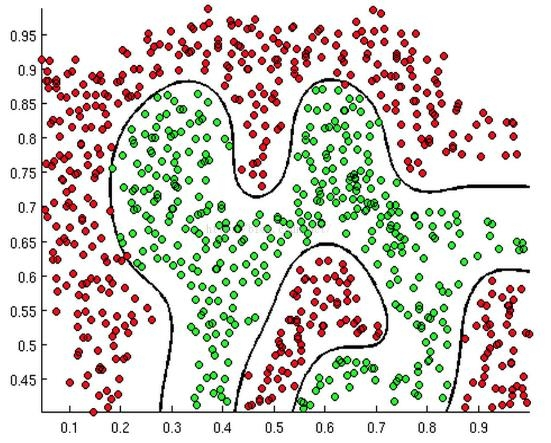
预测函数为：
对应概率解释：
十五、逻辑回归的似然与损失
似然函数：
对数似然：
转化为梯度下降的目标函数：
十六、逻辑回归的梯度
最终得到梯度：
参数更新公式：
十七、多分类 Softmax
Softmax 用于多分类问题，其基本思想是将线性输出映射为概率分布。
总结
逻辑回归真的真的很好用。