综合来看一共考过MLP、BP、CNN、RNN、GAN、ResNet、DBM。内容很多,因此采用功利性复习。
多层感知机(MLP)
原理
多层感知机是包含输入层、至少一个隐藏层、输出层的前馈神经网络,核心原理是:
- 结构:每层神经元与下一层全连接,输入层接收原始数据,隐藏层通过激活函数(如 Sigmoid、ReLU)引入非线性变换,输出层输出结果;
- 前向传播:输入数据经 "权重 × 输入 + 偏差" 计算后,通过激活函数传递到下一层,最终得到输出;
- 学习方式:通过反向传播算法,根据预测误差调整各层的权重和偏差,从而拟合复杂的非线性函数。
证明:(单层)感知机不能表示异或
单层感知机是线性分类器,仅能分隔 "线性可分" 的数据,而异或(XOR)是线性不可分的:
-
异或的真值表:
A(输入 1) B(输入 2) 异或结果 0 0 0 0 1 1 1 0 1 1 1 0 -
线性可分的定义:存在一条直线(二维情况),能将两类样本完全分开。把异或的样本画在二维平面上:(0,0)、(1,1) 为一类(结果 0),(0,1)、(1,0) 为另一类(结果 1)。显然无法用一条直线将这两类点分隔开,因此单层感知机(线性模型)无法表示异或。
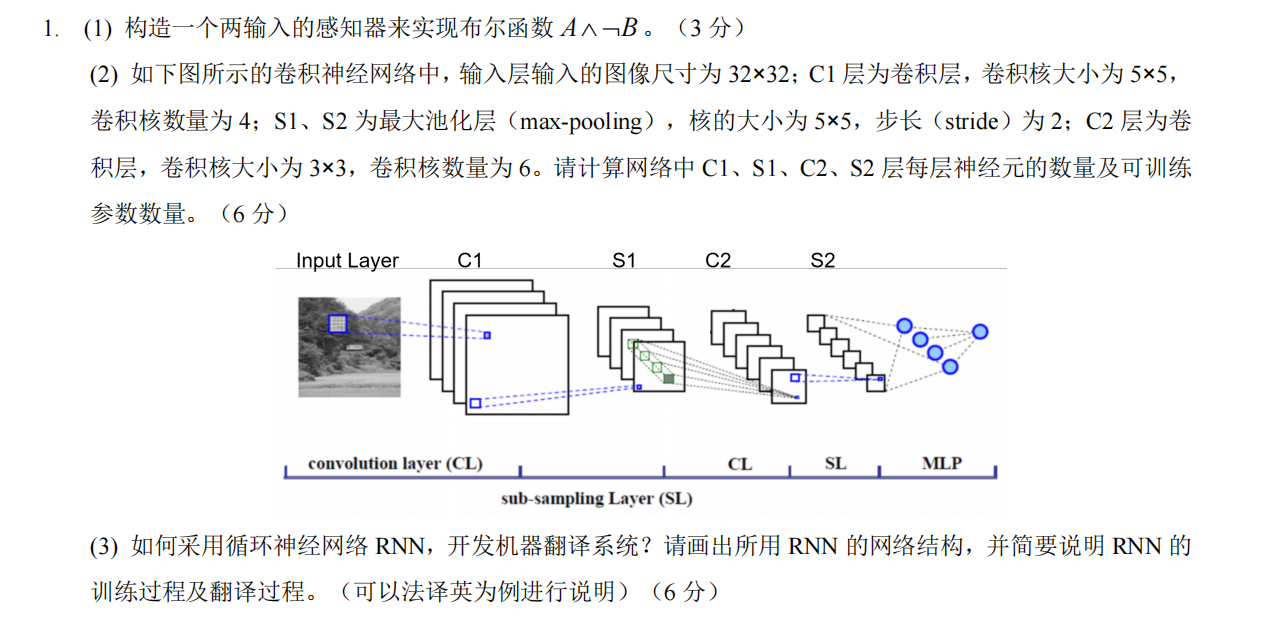
构造两输入感知器实现布尔函数 A∧¬B
感知器的模型为:y=sign(w1x1+w2x2+b)(其中 x1=A,x2=B,sign(z) 表示:z≥0 输出 1,z<0 输出 0)。
步骤 1:列 A∧¬B 的真值表
| A(x1) | B(x2) | ¬B | A∧¬B |
|---|---|---|---|
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
步骤 2:确定权重 、 和偏置 b
需要满足:
- 当 A=1,B=0 时,w1×1+w2×0+b≥0(输出 1);
- 其他情况,w1x1+w2x2+b<0(输出 0)。
选取一组简单参数:w1=1,w2=−1,b=−1,验证:
- A=0,B=0:1×0+(−1)×0−1=−1<0 → 输出 0(正确);
- A=0,B=1:1×0+(−1)×1−1=−2<0 → 输出 0(正确);
- A=1,B=0:1×1+(−1)×0−1=0≥0 → 输出 1(正确);
- A=1,B=1:1×1+(−1)×1−1=−1<0 → 输出 0(正确)。
最终感知器
输入为A、B,权重 w1=1(对应 A)、w2=−1(对应 B),偏置 b=−1,输出函数为:y=sign(A−B−1)即可实现 A∧¬B。
BP神经网络
相较于MLP,BP的改进在于多了反向传播
BP(误差反向传播)神经网络是一种通过 "前向计算输出、反向传递误差并优化参数" 学习的前馈神经网络,核心是用梯度下降法拟合输入到输出的映射关系,流程如下:
- 网络结构:由输入层(接收原始数据)、至少一个隐藏层(实现非线性变换)、输出层(输出预测结果)组成;层间神经元全连接,每个连接对应 "权重",每个神经元对应 "偏置"(权重和偏置是待学习的参数)。
- 前向传播:输入数据从输入层传递到隐藏层,通过 "权重 × 输入 + 偏置" 计算中间值,再经激活函数(如 Sigmoid、ReLU)转换为神经元输出;最终传递到输出层,得到预测结果。
- 误差计算:对比预测结果与真实标签,计算误差(如回归任务用均方误差,分类任务用交叉熵)。
- 反向传播 :从输出层往输入层反向推导,用链式求导法则计算各层参数(权重、偏置)对误差的梯度。
- 参数更新:通过梯度下降法,沿梯度反方向调整权重和偏置,减小误差;重复 "前向传播→误差计算→反向传播→参数更新",直到误差满足要求。
BP 神经网络遇到的困难
- 梯度问题(消失 / 爆炸):深层网络中,梯度经多层传递后急剧衰减(消失)或放大(爆炸),导致深层参数无法有效更新。
- 过拟合风险:当网络复杂、训练数据不足时,模型会拟合训练数据的噪声,对新数据的泛化能力差。
- 训练效率低:传统随机梯度下降(SGD)收敛慢;大批次训练占用内存高,小批次训练则会出现梯度波动。
- 调参复杂度高:隐藏层数量、神经元个数、学习率等超参数缺乏统一标准,依赖人工经验调试。
- 可解释性差:属于 "黑箱" 模型,难以解释各参数的实际意义与决策逻辑。
梯度消失的原因
梯度消失是深层 BP 网络中,深层参数的梯度趋近于 0 的现象,根源是反向传播的链式求导特性:在反向传播时,某层参数的梯度是 "后续层梯度 × 当前层激活函数的导数 × 当前层权重" 的乘积。以经典的 Sigmoid 激活函数为例:Sigmoid 的导数为 σ′(x)=σ(x)(1−σ(x)),其最大值仅为 0.25(当 x=0 时),且多数情况下小于 1;同时权重若初始化在 0 附近(避免输出饱和),权重值也小于 1。
当网络层数较多时,梯度会被 "每层的激活函数导数 × 权重" 不断缩小,经过多层传递后,深层参数的梯度会指数级衰减 (例如 10 层 Sigmoid 网络,每层乘 0.25,梯度会缩小到 (0.25)10≈9.5×10−7),几乎趋近于 0,而更新参数时,总会减去学习率×梯度,梯度缩小导致深层参数无法被有效更新,训练停滞。
CNN
CNN只考过计算题,因此只说如何计算
(1)先明确核心公式
- 输出尺寸公式(卷积 / 池化层通用,默认填充P=0):输出尺寸=( 输入尺寸−核大小 ) / 步长 + 1(结果非整数时,通常向下取整)
- 可训练参数公式 :
- 卷积层:(核尺寸×输入通道数+1)×卷积核数量(+1 是偏置项)
- 池化层:无参数(仅做特征下采样)
原理参考CNN参数计算,有动图好理解。
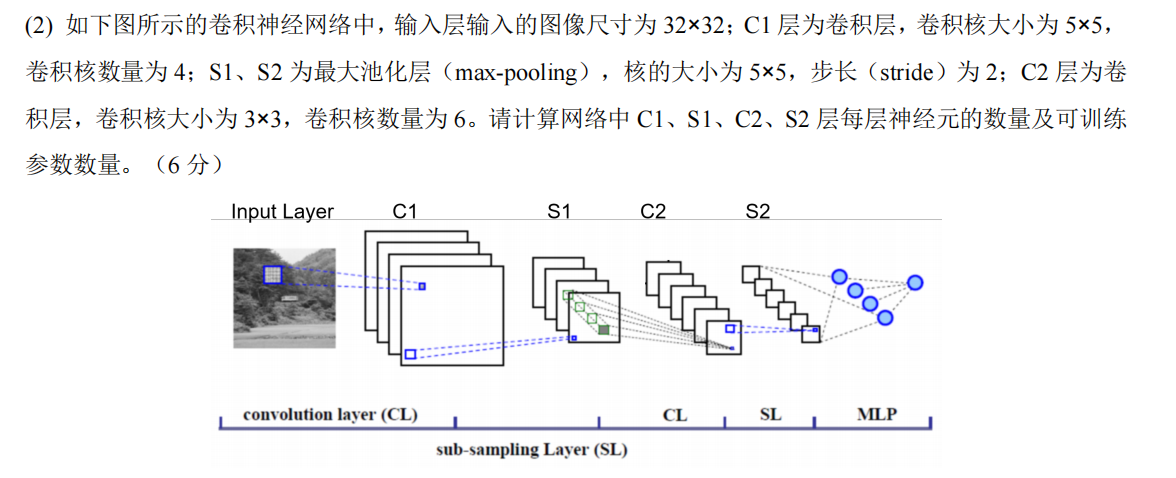
(2)逐层计算
默认输入图像为单通道(灰度图),输入尺寸32×32。
① C1 层(卷积层)
- 输入:32×32×1(通道数 = 1)
- 卷积核:5×5,数量 = 4,步长 = 1
- 输出尺寸:(32−5) / 1+1=28 → 特征图尺寸28×28
- 神经元数量:28×28×4=3136
- 可训练参数:(5×5×1+1)×4=26×4=104
② S1 层(最大池化层)
- 输入:28×28×4
- 池化核:5×5,步长 = 2
- 输出尺寸:(28−5) / 2+1≈12(向下取整)→ 特征图尺寸12×12
- 神经元数量:12×12×4=576
- 可训练参数:0(池化层无参数)
③ C2 层(卷积层)
- 输入:12×12×4(通道数 = 4)
- 卷积核:3×3,数量 = 6,步长 = 1
- 输出尺寸:(12−3) / 1+1=10 → 特征图尺寸10×10
- 神经元数量:10×10×6=600
- 可训练参数:(3×3×4+1)×6=37×6=222
④ S2 层(最大池化层)
- 输入:10×10×6
- 池化核:5×5,步长 = 2
- 输出尺寸:(10−5) / 2+1≈3(向下取整)→ 特征图尺寸3×3
- 神经元数量:3×3×6=54
- 可训练参数:0
RNN
1. 所用 RNN 的网络结构
采用RNN 编码器 - 解码器架构,流程如下:
- 编码器:由 RNN 组成,输入法语词序列(如 "Je mange une pomme"),逐词处理并更新隐状态,最终输出包含法语语义的 "上下文向量";
- 解码器:由 RNN 组成,以编码器的上下文向量为初始状态,接收已生成的英语词(训练时用目标序列前一词、翻译时用自身输出词),输出下一个英语词的概率。
2. RNN 的训练过程(以法译英为例)
- 准备法英平行语料,将句子拆分为词序列;
- 编码器逐词输入法语序列,得到上下文向量;
- 解码器采用强制教学策略:输入英语序列的前一个词,结合上下文向量输出当前词的概率;
- 计算预测词与真实词的误差,反向调整编码器、解码器的参数,重复训练至误差足够小。
3. 翻译过程(以法译英为例)
- 编码器输入待翻译的法语句子(如 "Je bois du café"),生成上下文向量;
- 解码器从句首符<sos>开始,结合上下文向量生成第一个英语词;
- 后续每一步,将已生成的英语词输入解码器,继续生成下一个词,直到生成句尾符 <<eos>;
- 去除<sos>和 <<eos>,得到最终翻译结果(如 "I drink coffee")。
GAN
一、GAN 的基本原理
GAN(生成对抗网络)核心是生成器(G)与判别器(D)的对抗与协同学习:
- 生成器(G):输入随机噪声,生成模仿真实数据分布的 "假数据"(如图像、文本),目标是让假数据尽可能接近真实数据,骗过判别器;
- 判别器(D):输入真实数据和生成器的假数据,输出 "数据为真" 的概率,目标是准确区分真实数据和假数据;
- 两者交替对抗:生成器不断优化以 "欺骗" 判别器,判别器不断优化以 "识破" 假数据,最终达到平衡 ------ 判别器无法区分真假(准确率接近 50%),生成器生成的数据与真实数据分布一致。
二、GAN 的学习算法
- 数据准备:收集目标真实数据(如人脸图像、法语 - 英语平行语料),作为判别器的 "真数据" 样本;
- 初始化参数:随机初始化生成器(G)和判别器(D)的网络参数(权重、偏置);
- 交替训练(核心环节) :
- 训练判别器(D):固定 G,将真实数据和 G 生成的假数据输入 D,计算 D 的分类误差(如交叉熵),通过梯度下降更新 D 的参数,提升区分真假的能力;
- 训练生成器(G):固定 D,将随机噪声输入 G 生成假数据,把假数据输入 D,计算 D 误判假数据为 "真" 的误差,通过梯度下降更新 G 的参数,提升生成假数据的逼真度;
- 终止训练:重复步骤 3,直到判别器对真假数据的区分准确率接近 50%(无法有效区分),或训练轮次达到预设值,停止训练。

选C。GAN 是生成式模型,但它不直接估计数据分布,而是通过生成器生成样本间接逼近真实数据分布(传统生成式模型如高斯混合模型会直接估计分布的概率密度)。
ResNet
原理(详细参考残差神经网络)
- 核心问题:传统深层网络(如 100 层以上)训练时,会出现 "退化"(训练误差上升)和梯度消失(深层参数无法更新),根源是深层梯度经多层传递后衰减或被复杂变换 "稀释"。
- 核心创新:残差连接(Skip Connection) :
- 引入 "恒等映射",让网络层学习 "残差"(真实输出与输入的差值),而非直接学习完整映射。
- 结构上,将某一层的输入直接跳过后续 1~2 层,与后续层的输出相加(即 "残差连接"),形成 "输入→变换层→输出 + 输入" 的路径。
- 梯度传播优势:反向传播时,梯度可通过残差连接 "直接短路" 回浅层,避免被多层权重和激活函数衰减,确保深层参数能有效更新;同时残差学习降低了网络的拟合难度(残差函数更易逼近零)。
DBM
网络结构
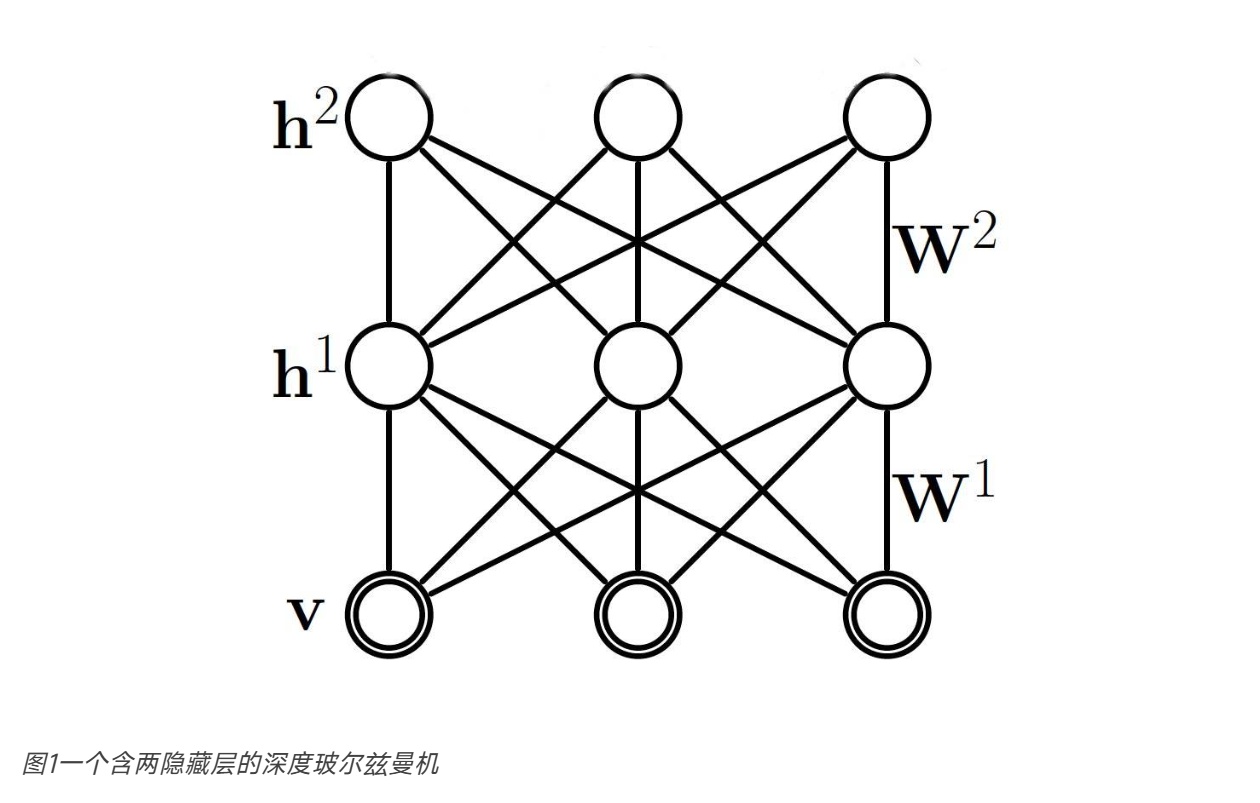
Deep Boltzmann Machines(DBM)是深度玻尔兹曼机,核心结构特点:
- 由 1 个可见层(接收输入数据)和多层隐藏层组成;
- 连接规则:层与层之间的神经元全连接,同一层内的神经元无连接;层间连接是对称的(无向),不存在单向依赖。
同层之间无连接,上下之间双向全连接。
学习算法
DBM 的学习分为 "预训练(逐层贪心初始化)" 和 "微调(全局优化)" 两个阶段:
- 预训练(逐层贪心训练):
- 将相邻的两层(如可见层 - 隐藏层 1、隐藏层 1 - 隐藏层 2)视为独立的受限玻尔兹曼机(RBM);
- 用 RBM 的对比散度(CD)算法逐层训练每一层对,得到模型的初始参数。
- 微调(全局优化):
- 利用平均场近似等方法,估计各隐藏层的状态(解决无向模型的层间双向依赖问题);
- 基于近似后的状态,用对比散度或随机最大似然等算法,调整所有层的连接参数,优化整个模型的对数似然,实现全局参数优化。
例题