这部分大题只考过格子游戏和田忌赛马
格子游戏
仅从做题的角度来说,这个是非常简单的,不需要理解贝尔曼方程中的参数意义,知道怎么往里代数就行了。
例题一

1、求状态估值

(注:该形式实际上是由于本题中所有策略行为的奖励都相同,因此可以将奖励从求和符号中提取出来,如果你发现和PPT上形式不一致,其实该形式是PPT上的化简,后面会给一个策略行为的奖励不同的例子。此外由于该题的收益衰减因子(即折扣因子为1)因此再在方程中省去了)
假设格子1的状态估值为、格子2、3、4的状态估值为
、
、
状态估值的含义:它是在当前策略下,从某个状态(比如某个格子)出发,未来能获得的累计奖励的期望值。
状态估值的作用:以玩家当前在格子2为例,其下一步可以有上下左右四种策略,如何决定呢?就看移动到哪状态估值最小,假设我们计算出 >
>
,那么下一步就会移动到
首先明确每个格子的动作转移规则(等概率选上下左右 4 个方向,出界则位置不变,出口估值为 0):
- 格子 1:左→出口(估值 0),右→格子 2,上→出界(留格子 1),下→出界(留格子 1)
- 格子 2:左→格子 1,右→格子 3,上→出界(留格子 2),下→出界(留格子 2)
- 格子 3:左→格子 2,右→出界(留格子 3),上→出口(估值 0),下→格子 4
- 格子 4:左→出界(留格子 4),右→出界(留格子 4),上→格子 3,下→出界(留格子 4)
由贝尔曼方程可以列出:


2、策略提升
策略提升的核心定义是:基于当前策略的状态估值,找到一个新策略,使得新策略下每个状态的价值不低于原策略 。本题中即改变策略------从四个方向等概率 改为 贪心
贪心策略是选择能使下一个状态估值最大的动作(因为V(s)=−1+V(s′),最大化V(s′)即最大化V(s)):
- 格子 1:下一个状态估值最大的是 "左(出口,0)"→ 贪心动作:左
- 格子 2:下一个状态估值最大的是 "左(格子 1,V1=−7)"→ 贪心动作:左
- 格子 3:下一个状态估值最大的是 "上(出口,0)"→ 贪心动作:上
- 格子 4:下一个状态估值最大的是 "上(格子 3,V3=−9)"→ 贪心动作:上
3、最优策略及最优状态估值
(会不会有 "非贪心" 的最优策略?:不会。如果一个策略不是基于最优估值的贪心策略,那么它在某个状态下选择的动作价值不是最大的,这会导致该状态的价值低于最优估值,因此不可能是最优策略。)
最优策略通过贝尔曼最优方程求解(选能最大化V(s′)的动作):
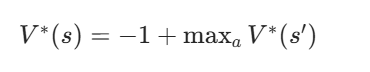
分析各格子的最优动作与估值:
- 格子 1:最优动作 "左(到出口)",V1∗=−1+0=−1
- 格子 3:最优动作 "上(到出口)",V3∗=−1+0=−1
- 格子 2:最优动作 "左(到格子 1)" 或 "右(到格子 3)",V2∗=−1+(−1)=−2
- 格子 4:最优动作 "上(到格子 3)",V4∗=−1+(−1)=−2
最优策略:
- 格子 1:左(到出口)
- 格子 2:左(到格子 1)/ 右(到格子 3)
- 格子 3:上(到出口)
- 格子 4:上(到格子 3)
最优状态估值:V1∗=−1,V2∗=−2,V3∗=−1,V4∗=−2
例题二

(1)策略评估(动态规划就是贝尔曼期望方程)
首先明确每个格子的动作转移(等概率选 4 个方向,出界则位置不变,出口估值为 0),列贝尔曼期望方程组:
步骤 1:分析每个格子的动作转移
- 格子 1:上→左出口(V=0),下→出界(留 1),左→出界(留 1),右→格子 2
- 格子 2:上→出界(留 2),下→格子 4,左→格子 1,右→格子 3
- 格子 3:上→右出口(V=0),下→出界(留 3),左→格子 2,右→出界(留 3)
- 格子 4:上→格子 2,下→出界(留 4),左→出界(留 4),右→出界(留 4)

(2)策略提升(贪心策略)
对每个格子,计算动作价值(q(s,a)=−1+V(s′)),选择价值最大的动作:
- 格子 1 :动作价值最大为 "上(到出口,q=−1+0=−1)"→ 贪心动作:上
- 格子 2 :动作价值最大为 "左(到 1,q=−1+(−8)=−9)" 或 "右(到 3,q=−1+(−8)=−9)"→ 贪心动作:左 / 右
- 格子 3 :动作价值最大为 "上(到出口,q=−1+0=−1)"→ 贪心动作:上
- 格子 4 :动作价值最大为 "上(到 2,q=−1+(−12)=−13)"→ 贪心动作:上
(3)最优策略及最优状态估值(贝尔曼最优方程)
最优策略通过 "选择能最大化下一个状态价值的动作" 确定,贝尔曼最优方程为 V∗(s)=−1+maxaV∗(s′):
最优动作分析
- 格子 1:最优动作 "上(到出口)"→ V1∗=−1+0=−1
- 格子 3:最优动作 "上(到出口)"→ V3∗=−1+0=−1
- 格子 2:最优动作 "左(到 1)" 或 "右(到 3)"→ V2∗=−1+(−1)=−2
- 格子 4:最优动作 "上(到 2)"→ V4∗=−1+(−2)=−3
最优策略
- 格子 1:上(到左出口)
- 格子 2:左(到 1)/ 右(到 3)
- 格子 3:上(到右出口)
- 格子 4:上(到 2)
最优状态估值
V1∗=−1,V2∗=−2,V3∗=−1,V4∗=−3
*例题三
(该题为PPT上的例子,实际考试中不可能考察这么复杂的例子,仅作为加深理解)
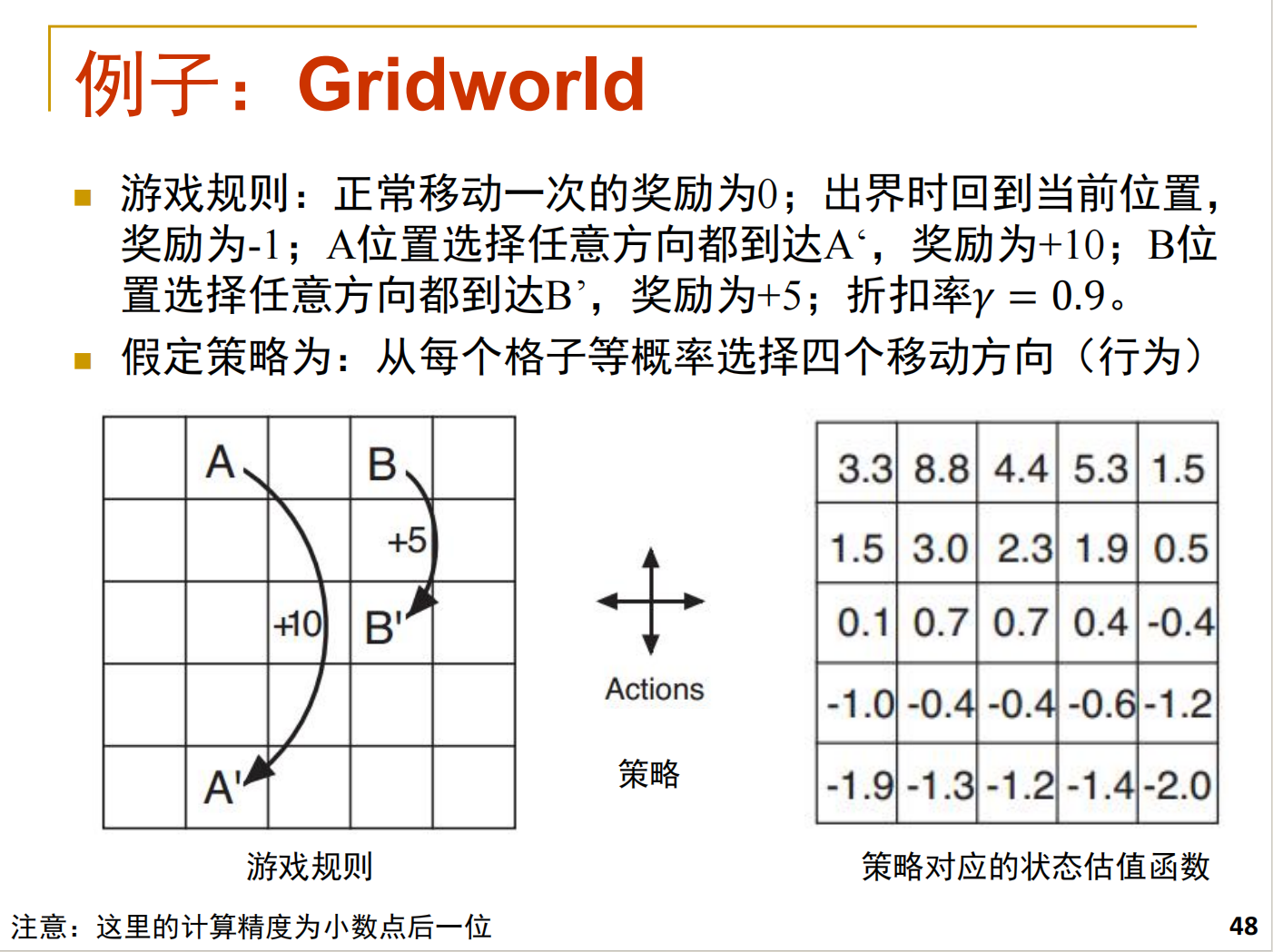
仅计算(1,2)和(1,1)作为说明,其余格子同理
明确游戏核心规则
- 动作:每个格子等概率选 "上下左右" 4 个方向(每个动作概率 = 1/4);
- 奖励:
- 正常移动(没出界):奖励 = 0;
- 出界(移动后超出 5×5 网格):奖励 =-1,且回到当前格子;
- 特殊格子 A(1,2):选任意方向都到 A'(5,2),奖励 =+10;
- 特殊格子 B(1,3):选任意方向都到 B',奖励 =+5;
- 折扣率:γ=0.9(未来奖励的衰减系数);
- 贝尔曼方程(等概率策略):V(s)=41∑a(ra+γ⋅V(sa′))(ra是动作a的奖励,sa′是动作a后的状态)。
计算特殊格子 (1,2) 的估值

计算普通格子 (1,1) 的估值
先分析 (1,1) 的 4 个动作对应的 "奖励 + 转移状态":
- 上:移动后出界(行 = 0)→ 奖励 =-1,转移回 (1,1);
- 下:移动到 (2,1)(行 = 2,列 = 1)→ 奖励 = 0,转移到 (2,1);
- 左:移动后出界(列 = 0)→ 奖励 =-1,转移回 (1,1);
- 右:移动到 (1,2)(即 A)→ 奖励 = 0,转移到 (1,2)。

这里可能有一个疑问,假如所有格子的状态估值函数没有给出,如何计算呢?
跟前两个简单例子一样,列方程,对应到该题中就是求解一个25元一次方程组 。(仅作了解 :实际中,这样的方程组往往很难求解,因此多采用迭代法:从初始估值(比如全 0)开始,反复用每个状态的贝尔曼方程更新估值,直到估值的变化小于阈值(收敛)。)
最优策略与最优估值函数

对于该题,采用方法一,之前的简单例子可以采取方法二。原因在于本题的场景非常复杂,贝尔曼最优方程并非线性方程组,求解起来很困难。
(为什么之前的题目不用方法一求解呢?其实也是可以的,不过前两个例子很简单,每个格子的最优动作直接指向出口或能一步到达出口的格子,不存在 "局部最优",而且对应的贝尔曼最优方程也很好计算,第一次贪心策略就是全局最优,无需多次迭代。)
下面进行求解
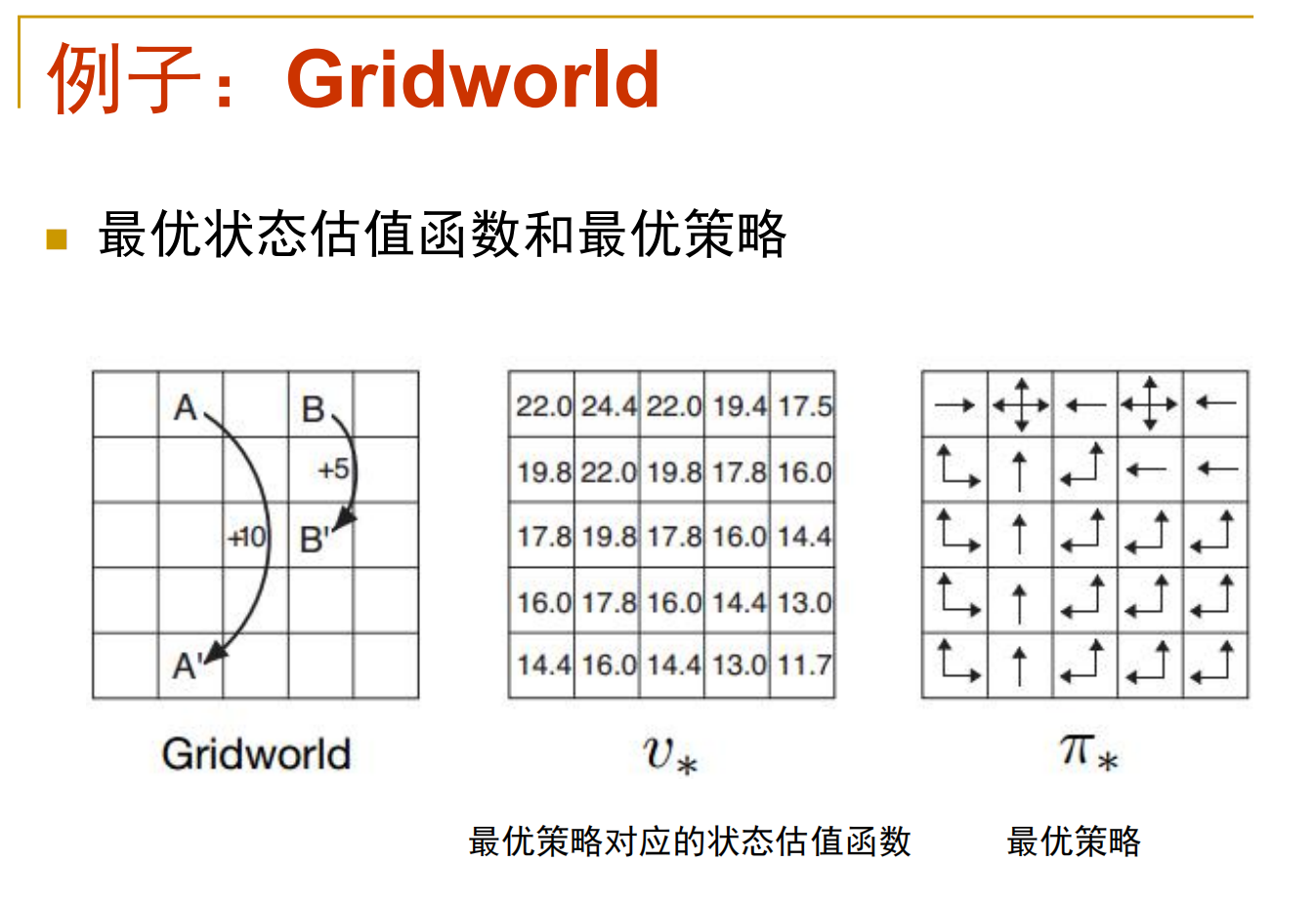
以格子 (1,1)、(1,2)(A)、(2,2)、(5,2)(A')为例,完整演示一轮迭代的数值变化:
初始状态
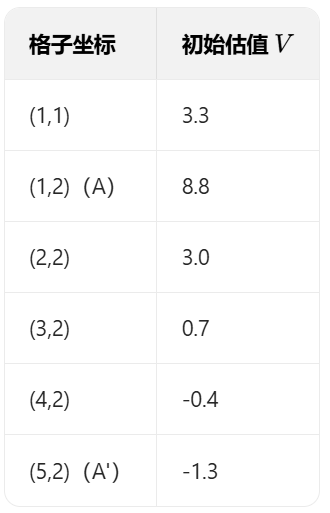
策略提升

策略评估


蚁群算法
偷个懒不写了,只给出答案,想具体了解的推荐一篇文章:
(20 封私信 / 1 条消息) 手把手实现蚁群算法:从数学原理到代码实践 - 知乎
核心原理
模拟蚂蚁觅食的协作行为:蚂蚁走的路径会留下 "信息素",路径越短、走的蚂蚁越多,信息素越浓;后续蚂蚁会优先选信息素浓的路径,最终群体通过信息素的动态积累与挥发,找到最优(最短)路径。
算法步骤
- 初始化:放一群蚂蚁,给所有路径初始信息素。
- 蚂蚁寻路:每只蚂蚁根据 "信息素浓度 + 路径长度" 选下一个节点,走完全程。
- 更新信息素:给找到的最优路径多加点信息素,所有路径的信息素会自然挥发一部分。
- 终止输出:重复迭代,直到找到稳定的最优路径。
适用场景
蚁群优化算法更适合离散空间的组合优化问题,典型场景包括:
- 旅行商问题(TSP)、车辆路径规划(VRP)等路径优化问题;
- 车间调度、任务分配等组合调度问题;
- 网络路由、图结构中的路径搜索问题。它的优势在于处理具有图结构的问题,但收敛速度较慢,易陷入局部最优。
粒子群算法
粒子群算法(PSO)小白笔记------详解、易懂、附案例代码-CSDN博客
核心原理
模拟鸟群 / 鱼群的群体运动:每个 "粒子" 代表一个候选解,它会记住自己找到的最好位置(个体最优)和整个群体找到的最好位置(全局最优),然后朝着这两个位置调整飞行方向和速度,逐步逼近最优解。
算法步骤
- 初始化:生成一群粒子,随机给它们初始位置和速度。
- 评估好坏:计算每个粒子当前位置的优劣(适应度)。
- 记录最优:每个粒子记自己的最好位置,整个群体记全局最好位置。
- 调整飞行:粒子根据 "惯性 + 个体经验 + 群体经验" 调整速度和位置,向最优位置靠近。
- 终止输出:重复迭代,直到找到稳定的最优解。
适用场景
粒子群优化算法更适合连续空间的优化问题,也可通过改进(如二进制 PSO)处理离散问题,典型场景包括:
- 函数优化(如高维、非线性函数的极值搜索);
- 神经网络参数优化、支持向量机参数调优;
- 工程优化(如结构设计、参数配置)、多目标优化问题。它的优势是收敛速度快、实现简单,但易陷入局部最优,对参数(如惯性权重)较敏感。