在一些生物信息任务上,经常会使用一些图算法,涉及大量循环计算(如图算法、动态规划、迭代优化等)。以前跑实验也遇到过一些问题:使用Matlab跑起来实在是很慢。当时组里有一些祖传的图算法代码(基于Matlab写的),但是效率很低。现在回过头来想想,应该是有更好的优化写法。在当下AI时代,使用Matlab的开源工具,几乎没看到了,除了Hinton这些老一辈的学者,新生代的基本都在用Python。我这里做一些测试------对比Python与Matlab的计算效率(在图算法相关的场景下),以便后续实验使用。

Python 与 Matlab对比
1 底层实现与数值计算库
- MATLAB :
(1)内置高度优化的线性代数库(如 Intel MKL、LAPACK、BLAS)。
(2)对矩阵运算原生支持,语法简洁,执行效率高。
(3)自动多线程并行(例如矩阵乘法、FFT 等操作)。 - Python :
(1)本身是解释型语言,纯 Python 循环效率较低。
(2)但通过 NumPy、SciPy、Numba、Cython 等库 可调用与 MATLAB 相当甚至更快的底层 C/Fortran 代码。
(3)NumPy 同样基于 BLAS/LAPACK(如 OpenBLAS、MKL),性能接近 MATLAB。
✅ 结论:在使用 NumPy/SciPy 的情况下,Python 的数值计算效率与 MATLAB 基本相当;若用纯 Python 循环,则远慢于 MATLAB。
2 JIT 编译与加速工具
- MATLAB :提供 codegen 工具可生成 C 代码,或使用 parfor 并行循环。
- Python :
(1)Numba:可对函数进行 JIT 编译(类似 MATLAB 的加速器),显著提升循环性能。
(2)Cython:允许混合 C 与 Python,接近 C 语言速度。
(3)Dask / Ray:用于大规模并行计算。
✅ 结论:Python 的生态在高性能计算方面更灵活,但需要额外配置;MATLAB 开箱即用。
3 GPU 与并行计算
- MATLAB:通过 Parallel Computing Toolbox 支持 GPU(gpuArray)和多核并行。
- Python:可通过 CuPy(NumPy 的 GPU 版本)、PyTorch、TensorFlow、JAX 等高效利用 GPU,生态更丰富,尤其在深度学习领域优势明显。
✅ 结论:GPU 计算方面,Python 生态更强大、灵活且免费。
两者对比:
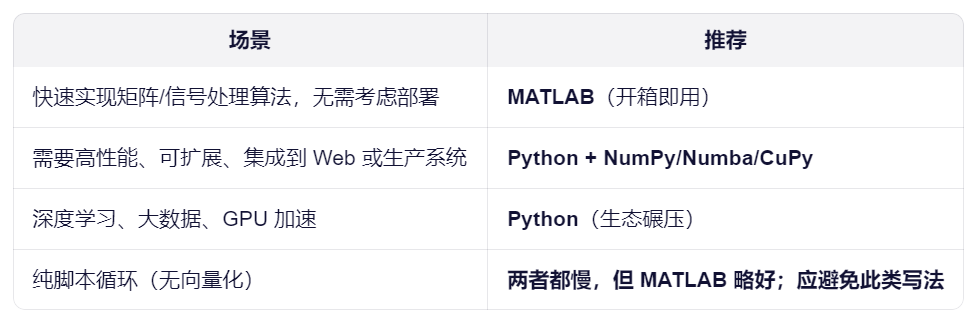
示例代码
示例1:大矩阵乘法
-
Python代码
pythonimport numpy as np import time N = 2000 A = np.random.rand(N, N) B = np.random.rand(N, N) start = time.time() C = A @ B # 或 np.dot(A, B) end = time.time() print(f"Python (NumPy) 矩阵乘法耗时: {end - start:.3f} 秒") -
Matlab代码
matlabN = 2000; A = rand(N); B = rand(N); tic; C = A * B; t = toc; fprintf('MATLAB 矩阵乘法耗时: %.3f 秒\n', t); -
测试结果:
Python (NumPy) 矩阵乘法耗时: 0.090 秒
MATLAB 矩阵乘法耗时: 0.080 秒
两者效率相当,Matlab效率略快。
示例2:计算两个向量的逐元素平方差之和(向量化 vs 显式循环)
-
Python
pythonimport numpy as np, time ### 向量化处理 N = 10_000_000 a = np.random.rand(N) b = np.random.rand(N) start = time.time() result = np.sum((a - b)**2) end = time.time() print(f"Python 向量化: {end - start:.4f} 秒, 结果={result:.2f}") ### 显式循环 import time N = 1_000_000 # 降低规模,否则太慢 a = [np.random.rand() for _ in range(N)] b = [np.random.rand() for _ in range(N)] start = time.time() s = 0.0 for i in range(N): s += (a[i] - b[i])**2 end = time.time() print(f"Python 纯循环: {end - start:.3f} 秒") -
Matlab
matlab% 向量化版本 N = 1e7; a = rand(N, 1); b = rand(N, 1); tic; result = sum((a - b).^2); t = toc; fprintf('MATLAB 向量化: %.4f 秒, 结果=%.2f\n', t, result); % for循环版本 clear N = 1e6; a = rand(N, 1); b = rand(N, 1); tic; s = 0; for i = 1:N s = s + (a(i) - b(i))^2; end t = toc; fprintf('MATLAB for 循环: %.3f 秒\n', t); -
输出结果
Python 向量化: 0.0702 秒
Python 纯循环: 5.668 秒
MATLAB 向量化: 0.0195 秒
MATLAB for 循环: 0.032 秒 -
初步结论 :
(1)MATLAB计算效率不管是向量化还是for循环,都是比纯python要高;
(2)Python向量化计算效率显著高于纯循环。但Python 本身并不天然适合向量化操作,但通过其强大的科学计算生态(尤其是 NumPy) ,Python 成为了进行高效向量化计算的主流语言之一。
(3)MATLAB 的 JIT 加速器(自 R2015b 起)对简单循环有优化,但仍远慢于向量化;应避免显式循环处理大规模数据。
示例3:计算数组中所有正数的立方和
-
Python代码
pythonimport numpy as np import numba as nb import time N = 10_000_000 x = np.random.randn(N) # 普通 Python 函数(慢) def cube_sum_slow(arr): s = 0.0 for v in arr: if v > 0: s += v ** 3 return s # Numba JIT 编译(快) @nb.jit(nopython=True) def cube_sum_fast(arr): s = 0.0 for v in arr: if v > 0: s += v ** 3 return s # 测试 start = time.time() res1 = cube_sum_slow(x) t1 = time.time() - start start = time.time() res2 = cube_sum_fast(x) # 首次编译稍慢,后续极快 t2 = time.time() - start print(f"Python 普通循环: {t1:.3f} 秒") print(f"Python + Numba: {t2:.3f} 秒") -
MATLAB代码
matlabclear,clc % 示例3:用 parfor 加速条件立方和 N = 1e7; x = randn(N, 1); % 标准正态分布,约一半为正数 % --- 普通 for 循环 --- tic; s_loop = 0; for i = 1:N if x(i) > 0 s_loop = s_loop + x(i)^3; end end t_loop = toc; % --- parfor 并行循环 --- % 确保已启动并行池(第一次会自动启动) tic; s_parfor = 0; parfor i = 1:N if x(i) > 0 s_parfor = s_parfor + x(i)^3; % MATLAB 自动识别为 reduction 变量 end end t_parfor = toc; % --- 向量化(作为性能上限参考)--- tic; s_vec = sum(x(x > 0).^3); t_vec = toc; % 输出结果 fprintf('N = %.0e\n', N); fprintf('普通 for 循环: %.4f 秒, 结果 = %.2f\n', t_loop, s_loop); fprintf('parfor 并行 : %.4f 秒, 结果 = %.2f\n', t_parfor, s_parfor); fprintf('向量化 : %.4f 秒, 结果 = %.2f\n', t_vec, s_vec); fprintf('结果一致? %s\n', mat2str(... (abs(s_loop - s_vec) < 1e-8) && (abs(s_parfor - s_vec) < 1e-8))); -
输出结果
- Python输出结果:
Python 普通循环: 1.472 秒
Python + Numba: 0.720 秒 - MATLAB输出结果:
普通 for 循环: 0.6704 秒, 结果 = 7977783.12
parfor 并行 : 56.8311 秒, 结果 = 7977783.12
向量化 : 0.1472 秒, 结果 = 7977783.12
结果一致? false
- Python输出结果:
-
初步结论 :
(1)Python使用Numba加速计算效率最高;Numba的使用可以参考博客:Python 提速大杀器之 numba 篇。
(2)MATLAB向量化计算效率高于普通的for循环;
(3)parfor 并行循环在这个示例中效率远低于普通循环。parfor更适合复杂的、计算更密集的循环计算。不是所有循环都适合并行,盲目使用 parfor 可能导致性能灾难。parfor的使用可以参考这篇博文:Matlab加速循环计算。
关于Numba有一些需要注意的:
- Numba 是一个 Python 的 JIT 编译器,主要用于加速 NumPy 风格的数值计算。
- 在深度学习中,它不用于模型训练本身(不支持自动微分) ,但可有效:
- 加速数据预/后处理(如 NMS、IoU、自定义指标)
- 快速实现高性能自定义算子(CPU 或 CUDA)
- 优化 CPU 端辅助计算(如数据增强、小批量推理)
- Numba 不能直接操作 PyTorch/TensorFlow 的 Tensor,需通过 NumPy 转换,且更适合类型明确、控制流简单的函数。
Numba 在深度学习中主要用于加速"周边"数值计算,而非核心模型训练。
图算法上的效率对比
在生物信息学(Bioinformatics)领域,图算法被广泛应用于基因组组装、蛋白质相互作用网络分析、代谢通路建模、系统发育树构建等多个方面。下面给出一些简单的示例。
示例一:floyd_warshall算法
-
Python代码
python# floyd_warshall_test.py import numpy as np import time from numba import njit @njit def floyd_warshall_numba(dist): n = dist.shape[0] for k in range(n): for i in range(n): for j in range(n): if dist[i, j] > dist[i, k] + dist[k, j]: dist[i, j] = dist[i, k] + dist[k, j] return dist def main(): N = 500 # 可调整:500, 800, 1000, 1500 np.random.seed(0) # 生成随机图:0 表示无边,用大数代替 inf A = np.random.rand(N, N) * 10 A[A < 0.7] = 1e9 # 稀疏化:70% 无连接 np.fill_diagonal(A, 0) # 拷贝用于测试 A_py = A.copy() # 预热(Numba JIT 编译) _ = floyd_warshall_numba(A_py[:10, :10]) # 正式计时 start = time.time() result = floyd_warshall_numba(A_py) end = time.time() print(f"Python + Numba (N={N}): {end - start:.3f} 秒") if __name__ == "__main__": main() -
MATLAB代码
matlab% floyd_warshall_test.m function floyd_warshall_test() N = 1500; % 与 Python 一致 rng(0); A = rand(N) * 10; A(A < 0.7) = inf; % 无连接设为 inf A(1:N+1:end) = 0; % 对角线为 0 tic; dist = A; for k = 1:N for i = 1:N for j = 1:N if dist(i,j) > dist(i,k) + dist(k,j) dist(i,j) = dist(i,k) + dist(k,j); end end end end elapsed = toc; fprintf('MATLAB (N=%d): %.3f 秒\n', N, elapsed); end -
实验结果
- 500节点:
Python + NumPy (N=500): 95.503 秒
Python + Numba (N=500): 0.247 秒
MATLAB (N=500): 0.260 秒 - 800节点:
Python + Numba (N=800): 0.495 秒
MATLAB (N=800): 1.076 秒 - 1000个节点:
Python + Numba (N=1000): 0.812 秒
MATLAB (N=1000): 2.117 秒 - 1500节点:
Python + Numba (N=1500): 2.593 秒
MATLAB (N=1500): 25.507 秒
从实验结果可以看出,在节点数为500(比较少)的时候,MATLAB计算效率与Python+Numba相当。随着节点数增加,Python+Numba的组合计算优势就很明显了。
- 500节点:
示例二:在大型稀疏网络中计算每个节点的局部聚类系数(Local Clustering Coefficient)
-
Python代码
python# clustering_coeff_test.py import igraph as ig import numpy as np import time def main(): N = 5000 # 节点数(比之前大,体现差异) p = 0.01 # 边概率(稀疏网络) # 生成 Erdős--Rényi 随机图 g = ig.Graph.Erdos_Renyi(n=N, p=p, directed=False) start = time.time() cc = g.transitivity_local_undirected() # 内置高效实现(C语言) elapsed = time.time() - start print(f"Python + igraph (N={N}, edges={g.ecount()}): {elapsed:.3f} 秒") print(f"Average clustering coefficient: {np.mean(cc):.4f}") if __name__ == "__main__": main() -
MATLAB代码
matlab% clustering_coeff_test.m function clustering_coeff_test() N = 5000; p = 0.01; A = sprand(N, N, p); % 稀疏邻接矩阵 A = A + A'; % 无向图 A = spones(A); % 二值化 A(1:N+1:end) = 0; % 去掉自环 tic; cc = zeros(N, 1); for i = 1:N neigh = find(A(i, :)); % 获取邻居 if length(neigh) < 2 cc(i) = 0; else subA = A(neigh, neigh); % 邻居子图 num_edges = nnz(tril(subA));% 子图中的边数 k = length(neigh); cc(i) = (2 * num_edges) / (k * (k - 1)); end end elapsed = toc; fprintf('MATLAB (N=%d, edges=%d): %.3f 秒\n', N, nnz(A)/2, elapsed); fprintf('Average clustering coefficient: %.4f\n', mean(cc)); end -
实验结果 Python + igraph (N=5000, edges=125188): 0.009 秒
Average clustering coefficient: 0.0100
MATLAB (N=5000, edges=247424): 1.938 秒
Average clustering : 0.0198
很明显,Python + igraph的计算效率远胜于MATLAB,差距可达100 多倍,更能体现Python生态优势。
我这里只是给出了一些比较简单示例。事实上现在有很多基于GNN的算法应用在生信场景上(很多发在子刊上),Python的优势体现得淋漓尽致。就目前我的观察来看,在真实的生信图分析场景(稀疏、不规则、需复杂拓扑计算)中,Python 的库生态(igraph, graph-tool, NetworkX + Numba)通常远胜 MATLAB。
- 主流生信流程(如 Snakemake、Nextflow)、数据库接口、命令行工具调用等,Python 集成更自然。
- 大多数高通量数据分析(RNA-seq、单细胞、网络分析)的现代工具栈以 Python 为主(如 Scanpy、Seurat 的 Python 版本)。
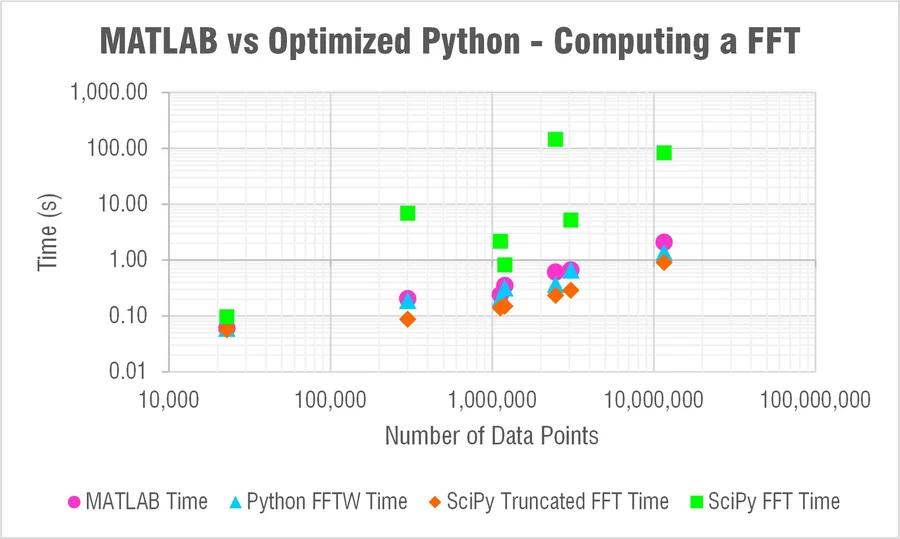
也有其他博客分析Python与MATLAB的计算效率对比,比如:MATLAB vs Python: Speed Test for Vibration Analysis。这篇博客分析FFT的计算效率,写得还挺有趣的。
以上仅供参考,欢迎关注交流。