题目描述
You are playing a game consisting of n planets. Each planet has a teleporter to another planet (or the planet itself).
You have to process q queries of the form: You are now on planet a and want to reach planet b. What is the minimum number of teleportations?
输入
The first input line contains two integers n and q: the number of planets and queries. The planets are numbered 1,2,...,n.
The second line contains n integers t1,t2,...,t_n: for each planet, the destination of the teleporter.
Finally, there are q lines describing the queries. Each line has two integers a and b: you are now on planet a and want to reach planet b.
Constraints
1 ≤ n, q ≤ 2*105
1 ≤ a,b ≤ n
输出
For each query, print the minimum number of teleportations. If it is not possible to reach the destination, print -1.
样例输入
5 3
2 3 2 3 2
1 2
1 3
1 4
样例输出
1
2
-1
题目大意: 接着上面这个题Planets Queries I,这个题是在求从a到b的最少步数。
**思路:**根据题意构造一个图,这个图有一个特征就是所有点的出度都为1,并且节点数=边数,这其实是一个基环内向森林。
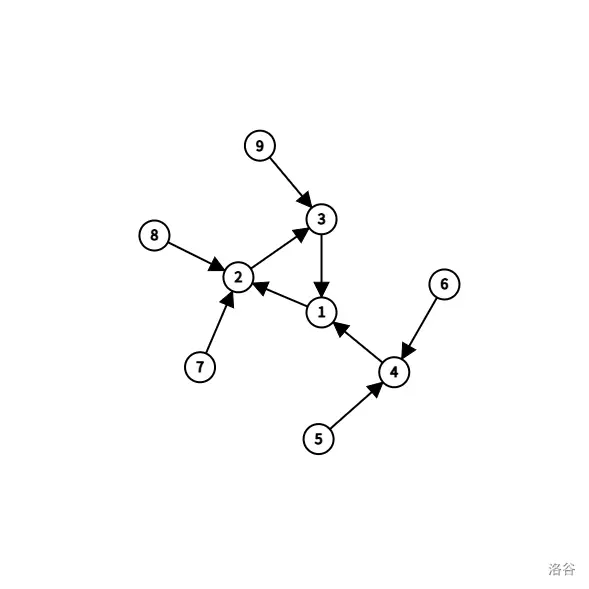
我们可以把它看成有若干个环,每个环上又有若干条链,环上的链和环本身组成了一个连通分支。要想从a到b,有这么几种情况:
1.a和b在不同连通分支上,显然没法到达
2.a和b都在链上,必须要保证 a,b 在同一条链上,并且 b 要比 a 更靠近环
3.a和b都在环上,直接给这个环上的节点进行编号,然后用他们的编号相减即可
4.一个在环上,一个在链上,必须是 a 在链上,b 在环上,从链上到环上才行;那最少步数就是 a 到环的最短步数 t + a 走 t 步到达的点 c 到 b 的最少步数(又转化成了3这种情况)而a 走 t 步到达的点 c 可以通过我们上一题的倍增方法解决
由上面的分析,可以看到我们需要知道的量有:节点在环上的编号,节点所在分支的编号,链上节点到环的最少步数。
直接dfs找环就行,由于每个点出边只有一条,也不需要用栈来存储。
cpp
#include <bits/stdc++.h>
using namespace std;
using ll=long long;
const int N=200010;
int t[N];
int dp[N][20];
int s[N];
int node[N],cycle[N],len[N];//节点在环里面的编号,节点在第几个环或环的链上
int d[N];//链上节点到环的最短距离
int fun(int a,int k){//从a走k步
for (int i=0;i<20;i++){
if(k&(1<<i))
a=dp[a][i];
}
return a;
}
int query(int a,int b){
if(cycle[a]!=cycle[b])//不同分支
return -1;
int nn=len[cycle[a]];
if(node[a]==-1&&node[b]==-1){//都在链上
int t=d[a]-d[b];
if(t<0||fun(a,t)!=b) return -1;//在同一条链上
return t;
}
if(node[a]==-1){//链上到环上
int t=d[a];
int c=fun(a,t);
return (node[b]-node[c]+nn)%nn+t;
}
if(node[a]!=-1&&node[b]!=-1){//环上到环上
return (node[b]-node[a]+nn)%nn;
}
return -1;
}
int main() {
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
int n,q;cin>>n>>q;
for(int i=1;i<=n;i++){
cin>>t[i];
dp[i][0]=t[i];
}
for (int j=1;j<20;j++){
for (int i=1;i<=n;i++){
dp[i][j]=dp[dp[i][j-1]][j-1];
}
}
memset(node,-1,sizeof(node));
int cycle_ans=0;
for (int i=1;i<=n;i++){
if(s[i]!=0) continue;
vector<int>path;
int cur=i;
while(1){
if(s[cur]==0){
s[cur]=1;
path.push_back(cur);
cur=t[cur];
continue;
}
if(s[cur]==1){//找到环
cycle_ans++;
int st=find(path.begin(),path.end(),cur)-path.begin();//环的起点
vector<int>temp(path.begin()+st,path.end());
len[cycle_ans]=temp.size();
for (int j=0;j<temp.size();j++){//环内的节点
node[temp[j]]=j;
cycle[temp[j]]=cycle_ans;
s[temp[j]]=2;
}
for (int j=st-1;j>=0;j--){//环外链上的节点
cycle[path[j]]=cycle_ans;
d[path[j]]=st-j;
s[path[j]]=2;
}
break;
}
if(s[cur]==2){//之前已经处理过的环
int ans=cycle[cur];
int dist=d[cur];
for (int j=path.size()-1;j>=0;j--){
cycle[path[j]]=ans;
d[path[j]]=++dist;
s[path[j]]=2;
}
break;
}
}
}
while(q--){
int a,b;cin>>a>>b;
cout<<query(a,b)<<'\n';
}
return 0;
}看了2个小时才看懂题解bush()