机器学习入门（十一）逻辑回归，分类问题评估

混淆矩阵

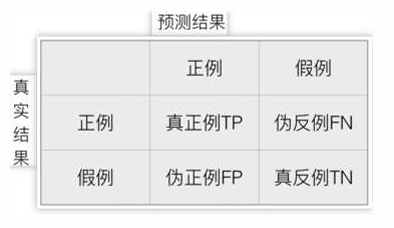
混淆矩阵四个指标

• 真实值是正例的样本中，被分类为正例的样本数量有多少，叫做真正例（TP，True Positive）

• 真实值是正例的样本中，被分类为假例的样本数量有多少，叫做伪反例（FN，False Negative）

• 真实值是假例的样本中，被分类为正例的样本数量有多少，叫做伪正例（FP，False Positive）

• 真实值是假例的样本中，被分类为假例的样本数量有多少，叫做真反例（TN，True Negative）

例

已知：样本集10样本，有 6 个恶性肿瘤样本，4 个良性肿瘤样本，我们假设恶性肿瘤为正例。

模型A：预测对了 3 个恶性肿瘤样本，4 个良性肿瘤样本请计算：TP、FN、FP、TN。

1.真正例 TP 为：3

2.伪反例 FN 为：3

3.伪正例 FP 为：0

4.真反例 TN：4

模型B：预测对了 6 个恶性肿瘤样本，1个良性肿瘤样本请计算：TP、FN、FP、TN

1.真正例 TP 为：6

2.伪反例 FN 为：0

3.伪正例 FP 为：3

4.真反例 TN：1

代码

python 复制代码

from sklearn.metrics import confusion_matrix
import pandas as pd


def dm01_confusion_matrix():
    # 2.构建数据，样本集中共有6个恶性肿瘤样本, 4个良性肿瘤样本
    y_true = ["恶性", "恶性", "恶性", "恶性", "恶性", "恶性", "良性", "良性", "良性", "良性"]
    # 3.1 混淆矩阵，模型 A: 预测对了3个恶性肿瘤样本, 4个良性肿瘤样本
    print("模型A:")

    print("-" * 13)
    y_pred1 = ["恶性", "恶性", "恶性", "良性", "良性", "良性", "良性", "良性", "良性", "良性"]
    result = confusion_matrix(y_true, y_pred1, labels=["恶性", "良性"])
    # print(result)
    print(pd.DataFrame(result, columns=["恶性(正例)", "良性(反例)"], index=["恶性(正例)", "良性(反例)"]))

    # 3.2 混淆矩阵，模型 B: 预测对了6个恶性肿瘤样本, 1个良性肿瘤样本
    print("模型B:")
    print("-" * 13)

    y_pred2 = ["恶性", "恶性", "恶性", "恶性", "恶性", "恶性", "恶性", "恶性", "恶性", "良性"]
    result = confusion_matrix(y_true, y_pred2, labels=["恶性", "良性"])
    print(pd.DataFrame(result, columns=["恶性(正例)", "良性(反例)"], index=["恶性(正例)", "良性(反例)"]))


dm01_confusion_matrix()

执行结果

python 复制代码

模型A:
-------------
        恶性(正例)  良性(反例)
恶性(正例)       3       3
良性(反例)       0       4
模型B:
-------------
        恶性(正例)  良性(反例)
恶性(正例)       6       0
良性(反例)       3       1

精确率

查准率，对正例样本的预测准确率。比如：把恶性肿瘤当做正例样本，想知道模型对恶性肿瘤的预测准确率。

例

已知：样本集10样本，有 6 个恶性肿瘤样本，4 个良性肿瘤样本，我们假设恶性肿瘤为正例。

模型A：预测对了 3 个恶性肿瘤样本，4 个良性肿瘤样本请计算：TP、FN、FP、TN

1.真正例 TP 为：3

2.伪反例 FN 为：3

3.伪正例 FP 为：0

4.真反例 TN：4

精度：3 / (3+0) = 100%

模型B：预测对了 6 个恶性肿瘤样本，1个良性肿瘤样本请计算：TP、FN、FP、TN

1.真正例 TP 为：6

2.伪反例 FN 为：0

3.伪正例 FP 为：3

4.真反例 TN：1

精度：6/(6+3) = 67%

代码

python 复制代码

from sklearn.metrics import precision_score


def dm02_precision_score():
    # 2.构建数据，样本集中共有6个恶性肿瘤样本, 4个良性肿瘤样本
    y_true = ["恶性", "恶性", "恶性", "恶性", "恶性", "恶性", "良性", "良性", "良性", "良性"]
    # 3.1 模型精确率评估，模型 A: 预测对了3个恶性肿瘤样本, 4个良性肿瘤样本
    y_pred1 = ["恶性", "恶性", "恶性", "良性", "良性", "良性", "良性", "良性", "良性", "良性"]
    result = precision_score(y_true, y_pred1, pos_label="恶性")
    print("模型A精度:", result)
    # 3.2 模型精确率评估，模型 B: 预测对了6个恶性肿瘤样本, 1个良性肿瘤样本
    y_pred2 = ["恶性", "恶性", "恶性", "恶性", "恶性", "恶性", "恶性", "恶性", "恶性", "良性"]
    result = precision_score(y_true, y_pred2, pos_label="恶性")
    print("模型B精度:", result)


dm02_precision_score()

执行结果

python 复制代码

模型A精度: 1.0
模型B精度: 0.6666666666666666

召回率(Recall)

也叫查全率，指的是预测为真正例样本占所有真实正例样本的比重例如：恶性肿瘤当做正例样本，则我们想知道模型是否能把所有的恶性肿瘤患者都预测出来。

计算方法：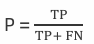

例：

已知：样本集10样本，有 6 个恶性肿瘤样本，4 个良性肿瘤样本，我们假设恶性肿瘤为正例。

模型A：预测对了 3 个恶性肿瘤样本，4 个良性肿瘤样本请计算：TP、FN、FP、TN。

1.真正例 TP 为：3

2.伪反例 FN 为：3

3.伪正例 FP 为：0

4.真反例 TN：4

召回率：3 / (3 + 3) = 50%

模型B：预测对了 6 个恶性肿瘤样本，1个良性肿瘤样本请计算：TP、FN、FP、TN。

1.真正例 TP 为：6

2.伪反例 FN 为：0

3.伪正例 FP 为：3

4.真反例 TN：1

召回率：6 / (6 + 0) = 100%

代码

python 复制代码

from sklearn.metrics import recall_score


def dm03_recall():
    # 2.构建数据，样本集中共有6个恶性肿瘤样本, 4个良性肿瘤样本
    y_true = ["恶性", "恶性", "恶性", "恶性", "恶性", "恶性", "良性", "良性", "良性", "良性"]
    # 3.1 模型召回率评估，模型 A: 预测对了3个恶性肿瘤样本, 4个良性肿瘤样本
    y_pred1 = ["恶性", "恶性", "恶性", "良性", "良性", "良性", "良性", "良性", "良性", "良性"]
    result = recall_score(y_true, y_pred1, pos_label="恶性")
    print("模型A召回率:", result)
    # 3.2 模型召回率评估，模型 B: 预测对了6个恶性肿瘤样本, 1个良性肿瘤样本
    y_pred2 = ["恶性", "恶性", "恶性", "恶性", "恶性", "恶性", "恶性", "恶性", "恶性", "良性"]
    result = recall_score(y_true, y_pred2, pos_label="恶性")
    print("模型B召回率:", result)


dm03_recall()

执行结果

python 复制代码

模型A召回率: 0.5
模型B召回率: 1.0

F1-score

若对模型的精度、召回率都有要求，查看模型在这两个评估方向的综合预测能力。

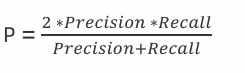
已知：样本集10样本，有 6 个恶性肿瘤样本，4 个良性肿瘤样本，我们假设恶性肿瘤为正例

模型A：预测对了 3 个恶性肿瘤样本，4 个良性肿瘤样本。

1.真正例 TP 为：3

2.伪反例 FN 为：3

3.伪正例 FP 为：0

4.真反例 TN：4

精度：100% 召回率：50%

F1-score = （2*1*0.5）/（1+0.5） = 67%

模型B：预测对了 6 个恶性肿瘤样本，1个良性肿瘤样本。

1.真正例 TP 为：6

2.伪反例 FN 为：0

3.伪正例 FP 为：3

4.真反例 TN：1

精度： 67% 召回率： 100

F1-score = （2* 0.67*1）/（0.67+1）= 80%

代码

python 复制代码

from sklearn.metrics import f1_score


def dm04_F1():
    # 2.构建数据，样本集中共有6个恶性肿瘤样本, 4个良性肿瘤样本
    y_true = ["恶性", "恶性", "恶性", "恶性", "恶性", "恶性", "良性", "良性", "良性", "良性"]
    # 3.1 模型F1-score评估，模型 A: 预测对了3个恶性肿瘤样本, 4个良性肿瘤样本
    y_pred = ["恶性", "恶性", "恶性", "良性", "良性", "良性", "良性", "良性", "良性", "良性"]
    result = f1_score(y_true, y_pred, pos_label="恶性")
    print("模型Af1-score:", result)
    # 3.2 模型F1-score评估，模型 B: 预测对了6个恶性肿瘤样本, 1个良性肿瘤样本
    y_pred = ["恶性", "恶性", "恶性", "恶性", "恶性", "恶性", "恶性", "恶性", "恶性", "良性"]
    result = f1_score(y_true, y_pred, pos_label="恶性")
    print("模型Bf1-score::", result)


dm04_F1()

执行结果

python 复制代码

模型Af1-score: 0.6666666666666666
模型Bf1-score:: 0.8

分类评估方法 --ROC曲线、AUC指标

真正率TPR与假正率FPR

1 正样本中被预测为正样本的概率TPR （True Positive Rate）

2 负样本中被预测为正样本的概率FPR （False Positive Rate）通过这两个指标可以描述模型对正/负样本的分辨能力

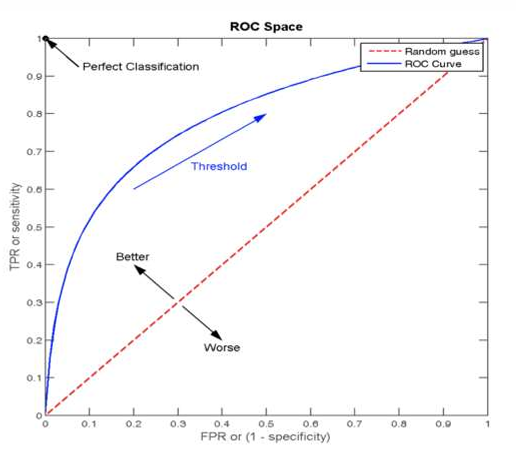
ROC曲线（Receiver Operating Characteristic curve）

是一种常用于评估分类模型性能的可视化工具。ROC曲线以模型的真正率TPR为纵轴，假正率FPR为横轴，它将模型在不同阈值下的表现以曲线的形式展现出来。

AUC (Area Under the Curve）- ROC曲线下面积

ROC曲线的优劣可以通过曲线下的面积（AUC）来衡量，AUC越大表示分类器性能越好。

当AUC=0.5时，表示分类器的性能等同于随机猜测。

当AUC=1时，表示分类器的性能完美，能够完全正确地将正负例分类。

ROC 曲线图像中，4 个特殊点的含义

点坐标说明：图像x轴FPR/y轴TPR, 任意一点坐标A(FPR值, TPR值)

1.点(0, 0)：所有的负样本都预测正确，所有的正样本都预测错误。相当于点的(FPR值0, TPR值0）

2.点(1, 0)：所有的负样本都预测错误，所有的正样本都预测错误。相当于点的(FPR值1, TPR值0) - 最差的效果

1.点(1, 1)：所有的负样本都预测错误，表示所有的正样本都预测正确。相当于点的(FPR值1，TPR值1)

2.点(0, 1)：所有的负样本都预测正确，表示所有的正样本都预测正确。相当于点的(FPR值0，TPR值1) - 最好的效果

例

已知：在网页某个位置有一个广告图片，该广告共被展示了 6 次；有 2 次被浏览者点击了。

其中正样本{1, 3} 负样本为{2, 4, 5, 6} 要求画出：在不同阈值下的ROC曲线。

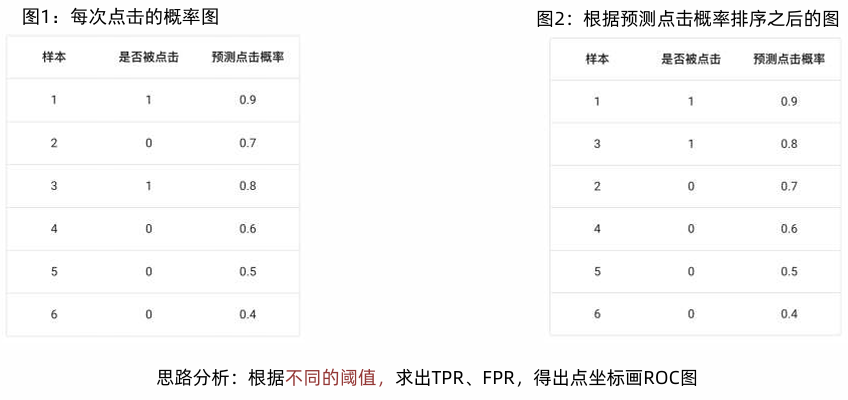
阈值	预测为正例的样本	TP	FN	FP	TN	TPR	FPR	TNR	FNR
0.9	无	0	2	0	4	0	0	1.0	1.0
0.8	1号	1	1	0	4	0.5	0	1.0	0.5
0.7	1号、3号	2	0	0	4	1.0	0	1.0	0.0
0.6	1号、3号、2号	2	0	1	3	1.0	0.25	0.75	0.0
0.5	1号、3号、2号、4号	2	0	2	2	1.0	0.5	0.5	0.0
0.4	1号、3号、2号、4号、5号	2	0	3	1	1.0	0.75	0.25	0.0

阈值：0.9

预测为正例的样本：无

TP = 0 (没有正确预测的正例)

FN = 2 (所有正例都被预测为负例：1号、3号)

FP = 0 (没有错误预测为正例的负例)

TN = 4 (所有负例都被正确预测：2号、4号、5号、6号)

TPR = TP/(TP+FN) = 0/(0+2) = 0

FPR = FP/(FP+TN) = 0/(0+4) = 0

TNR = TN/(TN+FP) = 4/(4+0) = 1.0

FNR = FN/(FN+TP) = 2/(2+0) = 1.0

阈值：0.8

预测为正例的样本：1号

TP = 1 (1号被正确预测为正例)

FN = 1 (3号被错误预测为负例)

FP = 0 (没有错误预测为正例的负例)

TN = 4

TPR = 1/(1+1) = 0.5

FPR = 0/(0+4) = 0

TNR = 4/(4+0) = 1.0

FNR = 1/(1+1) = 0.5

阈值：0.7

预测为正例的样本：1号、3号

TP = 2 (1号、3号都被正确预测为正例)

FN = 0 (所有正例都被正确预测)

FP = 0

TN = 4

TPR = 2/(2+0) = 1.0

FPR = 0/(0+4) = 0

TNR = 4/(4+0) = 1.0

FNR = 0/(0+2) = 0.0

阈值：0.6

预测为正例的样本：1号、3号、2号

TP = 2 (1号、3号被正确预测为正例)

FN = 0

FP = 1 (2号被错误预测为正例)

TN = 3 (4号、5号、6号被正确预测为负例)

TPR = 2/(2+0) = 1.0

FPR = 1/(1+3) = 0.25

TNR = 3/(3+1) = 0.75

FNR = 0/(0+2) = 0.0

阈值：0.5

预测为正例的样本：1号、3号、2号、4号

TP = 2 (1号、3号被正确预测为正例)

FN = 0

FP = 2 (2号、4号被错误预测为正例)

TN = 2 (5号、6号被正确预测为负例)

TPR = 2/(2+0) = 1.0

FPR = 2/(2+2) = 0.5

TNR = 2/(2+2) = 0.5

FNR = 0/(0+2) = 0.0

阈值：0.4

预测为正例的样本：1号、3号、2号、4号、5号

TP = 2 (1号、3号被正确预测为正例)

FN = 0

FP = 3 (2号、4号、5号被错误预测为正例)

TN = 1 (6号被正确预测为负例)

TPR = 2/(2+0) = 1.0

FPR = 3/(3+1) = 0.75

TNR = 1/(1+3) = 0.25

FNR = 0/(0+2) = 0.0

案例

• 已知：用户个人，通话，上网等信息数据

• 需求：通过分析特征属性确定用户流失的原因，以及哪些因素可能导致用户流失。建立预测模型来判断用户是否流失，并提出用户流失预警策略

0: "Churn" 客户转化率

1: "gender" 性别

2: "Partner_att" 配偶是否也为att用户

3: "Dependents_att" 家人是否为att用户

4: "landline" 是否使用att固定电话服务

5: "internet_att" 是否使用att互联网

6: "internet_other" 是否使用att互联网

7: "StreamingTV" 是否使用在线视频

8: "StreamingMovies" 是否使用在线电影

9: "Contract_Month" 是否使用月度合约

10: "Contract_1YR" 是否使用年度合约

11: "PaymentBank" 付款方式银行卡

12: "PaymentCreditcard" 付款方式信用卡

13: "PaymentElectronic" 付款方式微信支付宝

14: "MonthlyCharges" 每月花费

15: "TotalCharges" 累计花费

案例步骤分析

1、数据基本处理

• 主要是查看数据行/列数量

• 对类别数据数据进行one-hot处理

• 查看标签分布情况

2、特征筛选(特征工程)

• 分析哪些特征对标签值影响大

• 对标签进行分组统计，对比0/1标签分组后的均值等

• 初步筛选出对标签影响比较大的特征，形成x、y

3、模型训练

• 样本均衡情况下模型训练

• 样本不平衡情况下模型训练

• 交叉验证网格搜素等方式模型训练

4、模型评估

• 精确率

• ROC_AUC指标计算

代码

python 复制代码

import numpy as np
# 1.导入依赖包
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, roc_auc_score, classification_report


def dm01():
    churn_pd = pd.read_csv('./churn.csv')

    print(f'data.info-->{churn_pd.info}')
    print('churn_pd.describe()-->', churn_pd.describe())

    print('------------------------ churn_pd --------------------------')
    print(churn_pd.head(2))

    print('------------------------- source data ----------------------')
    data = pd.get_dummies(churn_pd)  # 转one-shot
    print(data.head(2))

    print('------------------------- filter data ----------------------')
    data = data.drop(['Churn_No', 'gender_Male'], axis=1)
    print(data.head(2))

    print('---------------------- data column change -------------------')
    data = data.rename(columns={'Churn_Yes': 'flag'})
    print(data.head(2))

    # 3.特征工程
    sns.countplot(data=data, y='Contract_Month', hue='flag')  # 绘图统计flag
    plt.show()

    x = data[[
        'Contract_Month',
        'internet_other',
        'Partner_att',
        'Dependents_att',
        'landline',
        'internet_att',
        'StreamingTV',
        'StreamingMovies',
        'Contract_1YR',
        'MonthlyCharges',
        'TotalCharges',
        'PaymentElectronic',
        'PaymentBank',
        'PaymentCreditcard',
    ]]
    y = data['flag']

    x_train, x_test, y_train, y_test = train_test_split(x, y, stratify=y, test_size=0.2, random_state=22)

    # 4.模型训练
    estimator = LogisticRegression(
        penalty='l2',  # L2正则化，防止过拟合
        C=1.0,  # 正则化强度倒数，越小正则化越强
        solver='lbfgs',  # 优化算法
        max_iter=1000,  # 增加迭代次数
        random_state=42,
        class_weight='balanced'  # 处理类别不平衡
    )
    estimator.fit(x_train, y_train)

    # 5.模型评估
    y_predict = estimator.predict(x_test)
    print('---------------------- accuracy_score --------------------')
    print(accuracy_score(y_test, y_predict), estimator.score(x_test, y_test))

    print('---------------------- roc_auc_score ----------------------')
    print(roc_auc_score(y_test, y_predict))

    print('----------------- classification_report -------------------')
    print(classification_report(y_test, y_predict))


dm01()

执行结果

python 复制代码

data.info--><bound method DataFrame.info of      Churn  gender  Partner_att  Dependents_att  landline  internet_att  ...  Contract_1YR  PaymentBank  PaymentCreditcard  PaymentElectronic  MonthlyCharges  TotalCharges
0       No  Female            1               0         0             1  ...             0            0                  0                  1           29.85         29.85
1       No    Male            0               0         1             1  ...             1            0                  0                  0           56.95       1889.50
2      Yes    Male            0               0         1             1  ...             0            0                  0                  0           53.85        108.15
3       No    Male            0               0         0             1  ...             1            1                  0                  0           42.30       1840.75
4      Yes  Female            0               0         1             0  ...             0            0                  0                  1           70.70        151.65
...    ...     ...          ...             ...       ...           ...  ...           ...          ...                ...                ...             ...           ...
7038    No    Male            1               1         1             1  ...             1            0                  0                  0           84.80       1990.50
7039    No  Female            1               1         1             0  ...             1            0                  1                  0          103.20       7362.90
7040    No  Female            1               1         0             1  ...             0            0                  0                  1           29.60        346.45
7041   Yes    Male            1               0         1             0  ...             0            0                  0                  0           74.40        306.60
7042    No    Male            0               0         1             0  ...             0            1                  0                  0          105.65       6844.50

[7043 rows x 16 columns]>
churn_pd.describe()-->        Partner_att  Dependents_att     landline  internet_att  internet_other  ...  PaymentBank  PaymentCreditcard  PaymentElectronic  MonthlyCharges  TotalCharges
count  7043.000000     7043.000000  7043.000000   7043.000000     7043.000000  ...  7043.000000        7043.000000        7043.000000     7043.000000   7043.000000
mean      0.483033        0.299588     0.903166      0.343746        0.439585  ...     0.219225           0.216101           0.335794       64.761692   2275.929881
std       0.499748        0.458110     0.295752      0.474991        0.496372  ...     0.413751           0.411613           0.472301       30.090047   2266.920469
min       0.000000        0.000000     0.000000      0.000000        0.000000  ...     0.000000           0.000000           0.000000       18.250000     18.800000
25%       0.000000        0.000000     1.000000      0.000000        0.000000  ...     0.000000           0.000000           0.000000       35.500000    392.575000
50%       0.000000        0.000000     1.000000      0.000000        0.000000  ...     0.000000           0.000000           0.000000       70.350000   1389.850000
75%       1.000000        1.000000     1.000000      1.000000        1.000000  ...     0.000000           0.000000           1.000000       89.850000   3778.525000
max       1.000000        1.000000     1.000000      1.000000        1.000000  ...     1.000000           1.000000           1.000000      118.750000   8684.800000

[8 rows x 14 columns]
------------------------ churn_pd --------------------------
  Churn  gender  Partner_att  Dependents_att  landline  internet_att  ...  Contract_1YR  PaymentBank  PaymentCreditcard  PaymentElectronic  MonthlyCharges  TotalCharges
0    No  Female            1               0         0             1  ...             0            0                  0                  1           29.85         29.85
1    No    Male            0               0         1             1  ...             1            0                  0                  0           56.95       1889.50

[2 rows x 16 columns]
------------------------- source data ----------------------
   Partner_att  Dependents_att  landline  internet_att  internet_other  StreamingTV  ...  MonthlyCharges  TotalCharges  Churn_No  Churn_Yes  gender_Female  gender_Male
0            1               0         0             1               0            0  ...           29.85         29.85      True      False           True        False
1            0               0         1             1               0            0  ...           56.95       1889.50      True      False          False         True

[2 rows x 18 columns]
------------------------- filter data ----------------------
   Partner_att  Dependents_att  landline  internet_att  internet_other  StreamingTV  ...  PaymentCreditcard  PaymentElectronic  MonthlyCharges  TotalCharges  Churn_Yes  gender_Female
0            1               0         0             1               0            0  ...                  0                  1           29.85         29.85      False           True
1            0               0         1             1               0            0  ...                  0                  0           56.95       1889.50      False          False

[2 rows x 16 columns]
---------------------- data column change -------------------
   Partner_att  Dependents_att  landline  internet_att  internet_other  StreamingTV  ...  PaymentCreditcard  PaymentElectronic  MonthlyCharges  TotalCharges   flag  gender_Female
0            1               0         0             1               0            0  ...                  0                  1           29.85         29.85  False           True    
1            0               0         1             1               0            0  ...                  0                  0           56.95       1889.50  False          False    

[2 rows x 16 columns]
---------------------- accuracy_score --------------------
0.7501774308019872 0.7501774308019872
---------------------- roc_auc_score ----------------------
0.7428634167764603
----------------- classification_report -------------------
              precision    recall  f1-score   support

       False       0.89      0.76      0.82      1035
        True       0.52      0.73      0.61       374

    accuracy                           0.75      1409
   macro avg       0.70      0.74      0.71      1409
weighted avg       0.79      0.75      0.76      1409