2024年3月GESP真题及题解(C++七级): 俄罗斯方块
题目描述
小杨同学用不同种类的俄罗斯方块填满了一个大小为 n × m n \times m n×m 的网格图。
网格图由 n × m n \times m n×m 个带颜色方块构成。小杨同学现在将这个网格图交给了你,请你计算出网格图中俄罗斯方块的种类数。
如果两个同色方块是四连通(即上下左右四个相邻的位置)的,则称两个同色方块直接连通;若两个同色方块同时与另一个同色方块直接或间接连通,则称两个同色方块间接连通。一个俄罗斯方块由一个方块和所有与其直接或间接连接的同色方块组成。定义两个俄罗斯方块的种类相同当且仅当通过平移其中一个俄罗斯方块可以和另一个俄罗斯方块重合;如果两个俄罗斯方块颜色不同,仍然视为同一种俄罗斯方块。
例如,在如下情况中,方块 1 1 1 和方块 2 2 2 是同一种俄罗斯方块,而方块 1 1 1 和方块 3 3 3 不是同一种俄罗斯方块。
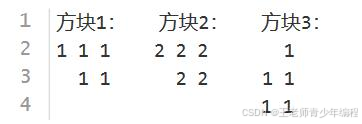
输入格式
第一行包含两个正整数 n n n 和 m m m,表示网格图的大小。
对于之后的 n n n 行,第 i i i 行包含 m m m 个正整数 a i 1 , a i 2 , ... a i m a_{i1}, a_{i2}, \dots a_{im} ai1,ai2,...aim,表示该行 m m m 个方块的颜色。
输出格式
输出一行一个整数表示答案。
输入输出样例 1
输入 1
5 6
1 2 3 4 4 5
1 2 3 3 4 5
1 2 2 3 4 5
1 6 6 7 7 8
6 6 7 7 8 8输出 1
7说明/提示
| 子任务 | 分数 | n , m ≤ n,m \leq n,m≤ | 特殊约定 |
|---|---|---|---|
| 1 1 1 | 30 30 30 | 20 20 20 | 所有俄罗斯方块大小不超过 5 × 5 5 \times 5 5×5 |
| 2 2 2 | 30 30 30 | 500 500 500 | 所有俄罗斯方块大小均为 1 × x 1 \times x 1×x 或 x × 1 x \times 1 x×1 类型,其中 x x x 是任意正整数 |
| 3 3 3 | 40 40 40 | 500 500 500 | 无 |
对全部的测试数据,保证 1 ≤ n , m ≤ 500 1 \leq n, m \leq 500 1≤n,m≤500, 1 ≤ a i , j ≤ n × m 1 \leq a_{i,j} \leq n \times m 1≤ai,j≤n×m。
思路分析
核心思路
统计网格中不同形状的连通块数量。关键点在于通过相对坐标 和标准化来识别形状,忽略颜色差异和位置平移。
算法流程
- 读取网格:存储颜色值
- 遍历每个未访问的格子:发现新连通块起点
- DFS搜索连通块 :
- 标记已访问
- 存储每个点相对于起点的坐标(相对坐标)
- 形状标准化:对相对坐标排序,消除遍历顺序影响
- 去重计数:使用set自动去重,最终set大小为不同形状数
代码实现
cpp
#include <bits/stdc++.h>
using namespace std;
const int N = 505;
int n, m;
int a[N][N]; // 网格颜色
int vs[N][N]; // 访问标记
int dx[4] = {-1, 1, 0, 0}; // 上下左右
int dy[4] = {0, 0, -1, 1};
// 当前连通块信息
int sx, sy; // 连通块起点
vector<pair<int, int>> block; // 相对坐标集合
/**
* DFS搜索同色连通块
* color 当前连通块颜色
* x,y 当前位置
* 功能:收集连通块所有点的相对坐标(相对于起点)
*/
void dfs(int color, int x, int y) {
vs[x][y] = 1;
// 存储相对坐标(当前点-起点)
block.push_back({x - sx, y - sy});
// 四方向搜索
for (int i = 0; i < 4; i++) {
int nx = x + dx[i];
int ny = y + dy[i];
// 边界检查、同色检查、未访问检查
if (nx >= 1 && nx <= n && ny >= 1 && ny <= m && a[nx][ny] == color && !vs[nx][ny]) {
dfs(color, nx, ny);
}
}
}
int main() {
cin >> n >> m;
// 读入网格
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
cin >> a[i][j];
memset(vs, 0, sizeof(vs));
set<vector<pair<int, int>>> s; // 形状集合(自动去重)
// 遍历所有格子
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (!vs[i][j]) { // 发现新连通块
sx = i; sy = j; // 设置起点
block.clear();
dfs(a[i][j], i, j); // 搜索连通块
// 标准化:排序确保相同形状有相同表示
sort(block.begin(), block.end());
s.insert(block); // 自动去重
}
}
}
cout << s.size() << endl; // 不同形状数量
return 0;
}功能分析
核心功能
判断两个连通块是否为同一种类(通过平移可以重合)。
关键技术点
-
相对坐标表示
cpp// 存储相对坐标而非绝对坐标 block.push_back({x - sx, y - sy});- 这样不同位置的相同形状会有相同的相对坐标集合
- 自动处理了平移等价性
-
形状标准化
cppsort(block.begin(), block.end());- 消除DFS遍历顺序的影响
- 确保相同形状的连通块有完全相同的坐标序列
-
自动去重
cppset<vector<pair<int, int>>> s;- 利用set自动去除重复形状
- 每个形状表示为排序后的相对坐标向量
时间复杂度
- DFS部分:O(n×m),每个格子访问一次
- 排序部分:每个连通块内部排序,总复杂度O(klogk),k为连通块总大小
- 总体复杂度:在网格大小500×500范围内可接受
空间复杂度
- 存储网格:O(n×m)
- DFS递归栈:最坏O(n×m)
- 形状存储:O(形状数×平均大小)
各种学习资料,助力大家一站式学习和提升!!!
cpp
#include<bits/stdc++.h>
using namespace std;
int main(){
cout<<"########## 一站式掌握信奥赛知识! ##########";
cout<<"############# 冲刺信奥赛拿奖! #############";
cout<<"###### 课程购买后永久学习,不受限制! ######";
return 0;
}1、csp信奥赛高频考点知识详解及案例实践:
CSP信奥赛C++动态规划:
https://blog.csdn.net/weixin_66461496/category_13096895.html点击跳转
CSP信奥赛C++标准模板库STL:
https://blog.csdn.net/weixin_66461496/category_13108077.html 点击跳转
信奥赛C++提高组csp-s知识详解及案例实践:
https://blog.csdn.net/weixin_66461496/category_13113932.html
2、csp信奥赛冲刺一等奖有效刷题题解:
CSP信奥赛C++初赛及复赛高频考点真题解析(持续更新):https://blog.csdn.net/weixin_66461496/category_12808781.html 点击跳转
CSP信奥赛C++一等奖通关刷题题单及题解(持续更新):https://blog.csdn.net/weixin_66461496/category_12673810.html 点击跳转
3、GESP C++考级真题题解:

GESP(C++ 一级+二级+三级)真题题解(持续更新):https://blog.csdn.net/weixin_66461496/category_12858102.html 点击跳转

GESP(C++ 四级+五级+六级)真题题解(持续更新):https://blog.csdn.net/weixin_66461496/category_12869848.html 点击跳转
GESP(C++ 七级+八级)真题题解(持续更新):
https://blog.csdn.net/weixin_66461496/category_13117178.html
4、CSP信奥赛C++竞赛拿奖视频课:
https://edu.csdn.net/course/detail/40437 点击跳转

· 文末祝福 ·
cpp
#include<bits/stdc++.h>
using namespace std;
int main(){
cout<<"跟着王老师一起学习信奥赛C++";
cout<<" 成就更好的自己! ";
cout<<" csp信奥赛一等奖属于你! ";
return 0;
}