DP 优化二：斜率优化 DP

铺垫。

在讲这个之前，我们先来看一道例题（选自洛谷）：

P2365 任务安排

题目描述

n n n 个任务排成一个序列在一台机器上等待完成（顺序不得改变），这 n n n 个任务被分成若干批，每批包含相邻的若干任务。

从零时刻开始，这些任务被分批加工，第 i i i 个任务单独完成所需的时间为 t i t_i ti。在每批任务开始前，机器需要启动时间
s s s，而完成这批任务所需的时间是各个任务需要时间的总和（同一批任务将在同一时刻完成）。

每个任务的费用是它的完成时刻乘以一个费用系数 f i f_i fi。请确定一个分组方案，使得总费用最小。

输入格式

第一行一个正整数 n n n。 第二行是一个整数 s s s。

下面 n n n 行每行有一对数，分别为 t i t_i ti 和 f i f_i fi，表示第 i i i 个任务单独完成所需的时间是 t i t_i ti 及其费用系数
f i f_i fi。

输出格式

一个数，最小的总费用。

输入输出样例 #1

输入 #1

5
1
1 3
3 2
4 3
2 3
1 4

输出 #1

153

说明/提示

【数据范围】 对于 100 % 100\% 100% 的数据， 1 ≤ n ≤ 5000 1\le n \le 5000 1≤n≤5000， 0 ≤ s ≤ 50 0 \le s \le 50 0≤s≤50， 1 ≤ t i , f i ≤ 100 1\le t_i,f_i \le 100 1≤ti,fi≤100。

【样例解释】 如果分组方案是 { 1 , 2 } , { 3 } , { 4 , 5 } \{1,2\},\{3\},\{4,5\} {1,2},{3},{4,5}，则完成时间分别为
{ 5 , 5 , 10 , 14 , 14 } \{5,5,10,14,14\} {5,5,10,14,14}，费用 C = 15 + 10 + 30 + 42 + 56 C=15+10+30+42+56 C=15+10+30+42+56，总费用就是 153 153 153。

这是一道很简单的 DP 题：我们设 f i , j f_{i,j} fi,j 表示进行到第 i i i 个任务且前面的任务被分成了 j j j 批所用的最小费用。那么可以得到如下的转移方程：

f i , j = min ⁡ k = 1 i { f k − 1 , j + ( s × j + ∑ l = 1 i t l ) × ∑ l = k i f l } f_{i,j}=\min_{k=1}^i\{f_{k-1,j}+(s\times j+\sum_{l=1}^it_l)\times\sum_{l=k}^if_l\} fi,j=k=1mini{fk−1,j+(s×j+l=1∑itl)×l=k∑ifl}

那两个求和明显可以改成前缀和，因此我们可以写成这样：

f i , j = min ⁡ k = 1 i { f k − 1 , j + ( s × j + s t i ) × ( s f i − s f k − 1 ) } f_{i,j}=\min_{k=1}^i\{f_{k-1,j}+(s\times j+st_i)\times(sf_i-sf_{k-1})\} fi,j=k=1mini{fk−1,j+(s×j+sti)×(sfi−sfk−1)}

然后这里介绍一种费用预先处理 思想，也就是说：我已经确定了 i i i 肯定会被分成一个批次，说明我当前这里对后面的所有数肯定都会有贡献，于是我们可以把后面所有的贡献全部算在这一批次上面。于是我们把 DP 定义改成： f i f_i fi 表示前 i i i 个物品分成若干批次时的最小代价。那么状态转移方程应该为：

f i = min ⁡ j = 1 i { f j − 1 + s t i × ( s f i − s f j − 1 ) + s × ( s f n − s f j − 1 ) } f_i=\min_{j=1}^{i}\{f_{j-1}+st_i\times(sf_i-sf_{j-1})+s\times(sf_n-sf_{j-1})\} fi=j=1mini{fj−1+sti×(sfi−sfj−1)+s×(sfn−sfj−1)}

其中， s × ( s f n − s f j − 1 ) s\times(sf_n-sf_{j-1}) s×(sfn−sfj−1) 就是费用预先处理的那一部分，因为既然 [ j , i ] [j,i] [j,i] 这一部分已经被划为一个批次了，那么对于 [ j , n ] [j,n] [j,n] 的所有商品来说：它们都需要多等一个 s s s 的时间。所以就把这部分费用预先处理了。

其实根据这个费用预先处理思想，我们会发现这个 DP 中间的所有值全都是错的，但是最终的答案是对的，也就是说：这种思想只能用于算答案，而不能算中间过程。

时间复杂度： O ( n 2 ) O(n^2) O(n2)。可过此题。

现在我们考虑一个难一点的题：

P10979 任务安排 2

题目背景

本题是 P2365 强化版，是 P5785 弱化版，用于让学生循序渐进地了解斜率优化 DP。

题目描述

机器上有 n n n 个需要处理的任务，它们构成了一个序列。这些任务被标号为 1 1 1 到 n n n，因此序列的排列为 1 , 2 , 3 ⋯ n 1 , 2 , 3 \cdots n 1,2,3⋯n。这 n n n 个任务被分成若干批，每批包含相邻的若干任务。从时刻 0 0 0 开始，这些任务被分批加工，第 i i i

个任务单独完成所需的时间是 T i T_i Ti。在每批任务开始前，机器需要启动时间 s s s，而完成这批任务所需的时间是各个任务需要时间的总和。

注意，同一批任务将在同一时刻完成 。每个任务的费用是它的完成时刻乘以一个费用系数 C i C_i Ci。

请确定一个分组方案，使得总费用最小。

输入格式

第一行一个整数 n n n。第二行一个整数 s s s。

接下来 n n n 行，每行有一对整数，分别为 T i T_i Ti 和 C i C_i Ci，表示第 i i i 个任务单独完成所需的时间是 T i T_i Ti 及其费用系数
C i C_i Ci。

输出格式

一行，一个整数，表示最小的总费用。

输入输出样例 #1

输入 #1

5
1
1 3
3 2
4 3
2 3
1 4

输出 #1

153

说明/提示

对于 100 % 100\% 100% 数据， 1 ≤ n ≤ 3 × 10 5 1 \le n \le 3 \times 10^5 1≤n≤3×105， 1 ≤ s ≤ 2 8 1 \le s \le 2^8 1≤s≤28， 1 ≤ T i ≤ 2 8 1\le T_i \le 2^8 1≤Ti≤28， 0 ≤ C i ≤ 2 8 0 \le C_i \le 2^8 0≤Ci≤28。

注意： 1 ≤ n ≤ 3 × 10 5 1\le n\le 3\times10^5 1≤n≤3×105。刚刚的方法已经不适用了！于是引出了斜率优化 DP。

斜率优化 DP

斜率优化 DP，是针对于转移方程类似于 f i = min ⁡ { Y ( j ) − K ( i ) X ( j ) } + C ( i ) f_i=\min\{Y(j)-K(i)X(j)\}+C(i) fi=min{Y(j)−K(i)X(j)}+C(i) 的 DP 题目。其中 Y ( j ) , X ( j ) Y(j),X(j) Y(j),X(j) 是关于 j j j 的两个函数， K ( i ) , C ( i ) K(i),C(i) K(i),C(i) 是关于 i i i 的两个函数。

对于这种转移方程，我们会发现普通的单调队列优化是不起作用的，因为 K ( i ) K(i) K(i) 这个函数一直在变。现在我们做这样几个操作。

首先，把 C ( i ) C(i) C(i) 移项，并把右半边看做一个新函数 B ( i ) B(i) B(i)：

B ( i ) = min ⁡ { Y ( j ) − K ( i ) X ( j ) } B(i)=\min\{Y(j)-K(i)X(j)\} B(i)=min{Y(j)−K(i)X(j)}

然后我们假定右半边已经是最小了，得到这样一个等式：

B ( i ) = Y ( j ) − K ( i ) X ( j ) B(i)=Y(j)-K(i)X(j) B(i)=Y(j)−K(i)X(j)

移项整理得：

K ( i ) X ( j ) + B ( i ) = Y ( j ) K(i)X(j)+B(i)=Y(j) K(i)X(j)+B(i)=Y(j)

我们会发现：这其实就是一个经典的一次函数。而我们要求的，实际上是这个一次函数的截距。

因为我们有很多个 j j j，所以我们可以得到很多个点 ( X ( j ) , Y ( j ) ) (X(j),Y(j)) (X(j),Y(j))：

因为我们要求的是截距，也就是说：截距是不固定的。所以我们过每个点做一条直线，并且这些直线互相平行（因为斜率一定）：

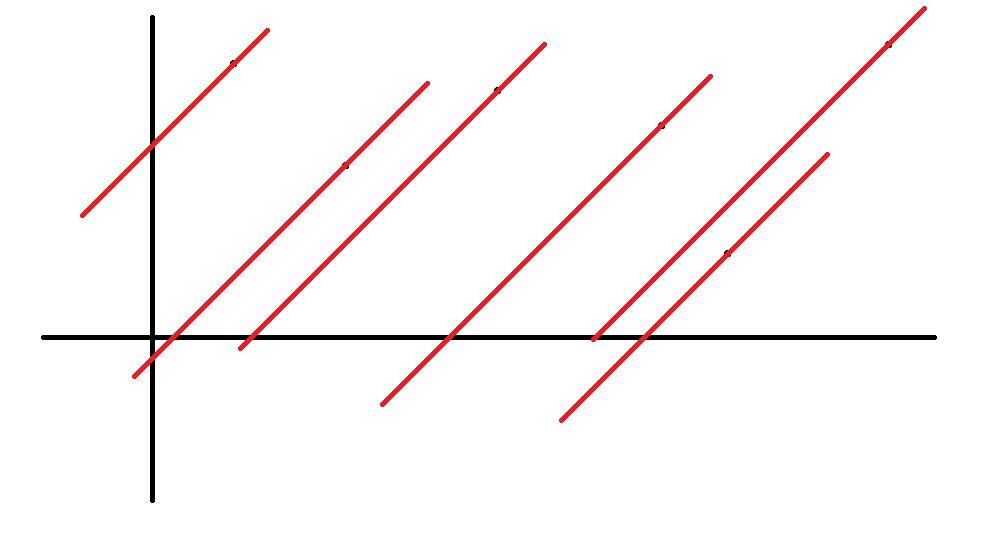
很明显，最靠底下的那一条线的截距最小，所以我们得到了截距的最小值。

但是我们不可能真的把这些点保存下来，然后一个一个算它们的截距。因此我们需要找到这个截距大小和点之间的关系。

首先假设我们有两个点：

过这两个点做两条平行直线：

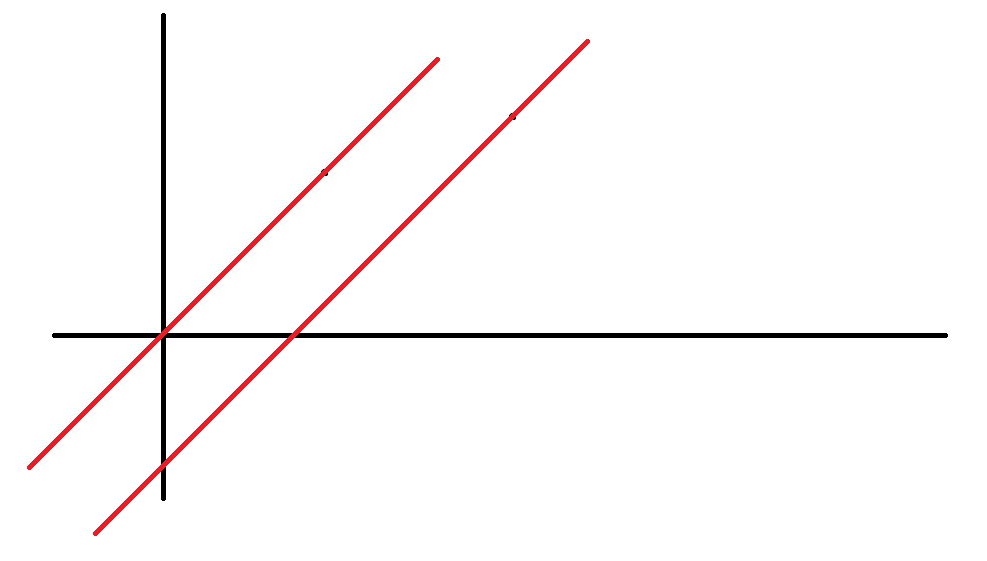
现在尝试想象这两条直线在旋转，并且保持平行。于是会出现下面三种情况：

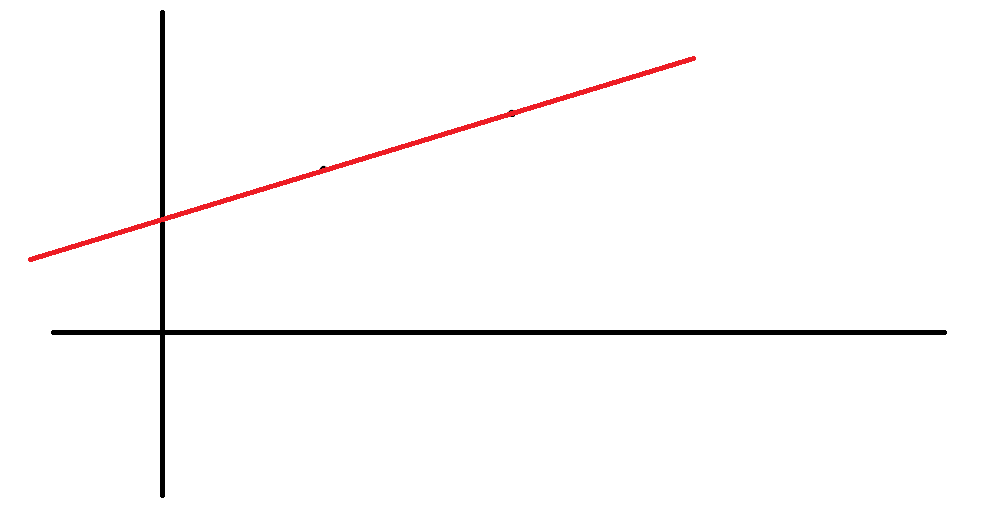
为了方便，我们设同时经过这两点的直线的斜率为 k k k，于是得到这样一个结论：当 K ( i ) > k K(i)>k K(i)>k 时，靠右的点的截距更小；当 K ( i ) = k K(i)=k K(i)=k 时，两点均可；当 K ( i ) < k K(i)<k K(i)<k 时，靠左的点的截距更小。

当然，这是两个点之间的关系，如果上升到更多的点，我们就要考虑一下哪些点有用了。

现在假设有三个点：

为了方便，我们从左到右依次记为 A , B , C A,B,C A,B,C。

假设 B B B 一定在直线 A C AC AC 的上面，且一定是中间的那个点，那么我们很容易得到： k A B > k A C > k B C k_{AB}>k_{AC}>k_{BC} kAB>kAC>kBC。

那么当 K ( i ) > k A B K(i)>k_{AB} K(i)>kAB 时，相对于 A A A 选 B B B 一定更小，因为 K ( i ) > k B C K(i)>k_{BC} K(i)>kBC，所以相对于 B B B 选 C C C 一定更小。所以选 C C C 点。

当 k A B > K ( i ) > k A C k_{AB}>K(i)>k_{AC} kAB>K(i)>kAC 时，相对于 B B B 选 A A A 一定更小，因为 K ( i ) > k A C K(i)>k_{AC} K(i)>kAC，所以相对于 A A A 选 C C C 一定更小，所以选 C C C 点。

当 k A C > K ( i ) > k B C k_{AC}>K(i)>k_{BC} kAC>K(i)>kBC 时，相对于 C C C 选 A A A 一定更小，因为 K ( i ) < k A B K(i)<k_{AB} K(i)<kAB，所以相对于 B B B 选 A A A 一定更小，所以选 A A A 点。

当 K ( i ) < k B C K(i)<k_{BC} K(i)<kBC 时，相对于 B B B 选 C C C 一定更小，因为 K ( i ) < k A C K(i)<k_{AC} K(i)<kAC，所以相对于 C C C 选 A A A 一定更小，所以选 A A A 点。

综上所述：最小值一定在 A A A 点和 C C C 点，而不可能在 B B B。

经过我们的"不严谨"证明，我们很容易发现这样一个事：如果有一个点在某两个点所在直线的上方并且在这两个点之间，那么这个点一定不会被作为最优解。

换句话说：就是当形成了这样的图时，我们肯定不会选中间那个点为最优点：

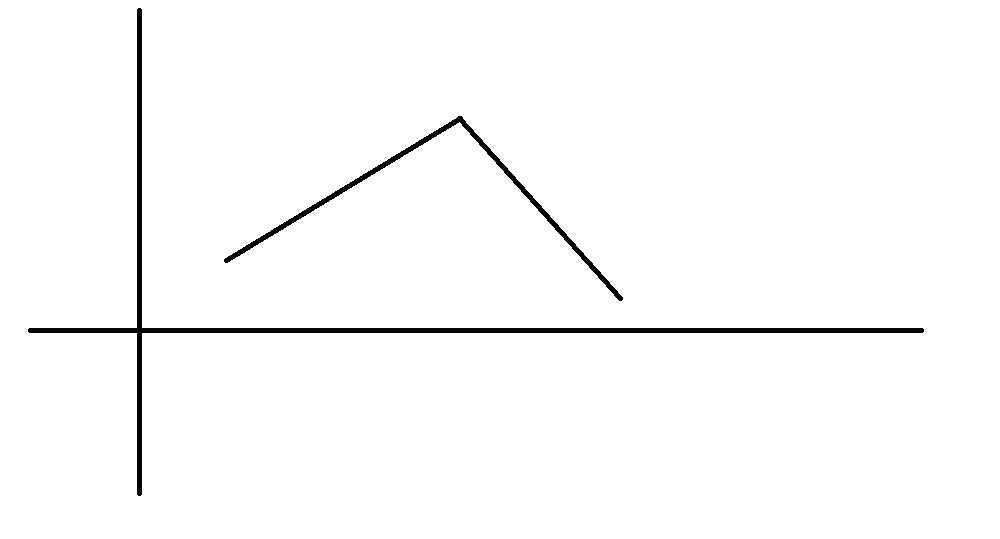
如果这两个点之间有很多个点并且都在它们所在横线上方，像这样：

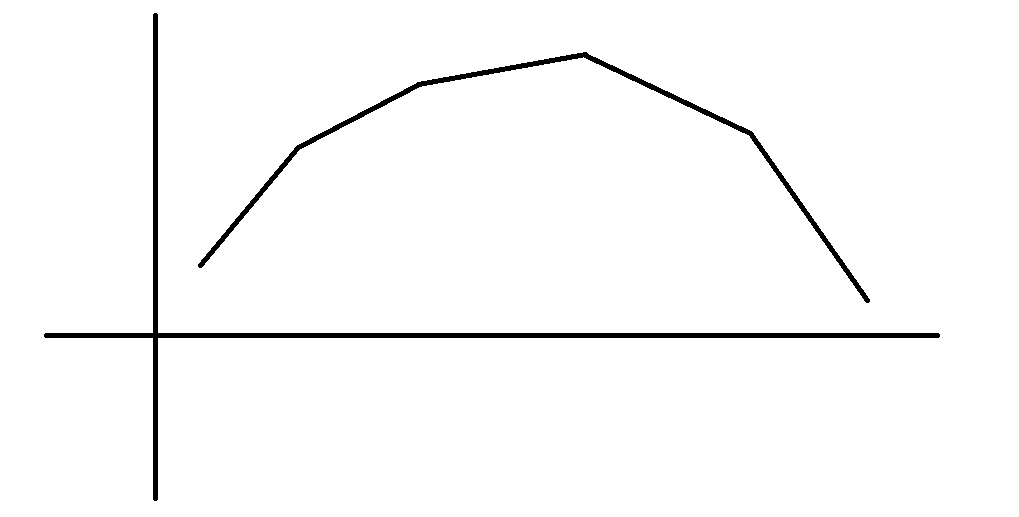
那么中间这些点肯定都不是最优解。其中，我们把上面的这个图形叫做凸包，因为它是向上凸出的，所以称之为"上凸包"。

也就是说：我们要保证我们的最优解集合里所有点连起来肯定不会形成上凸包，反之，我们要形成下凸包：

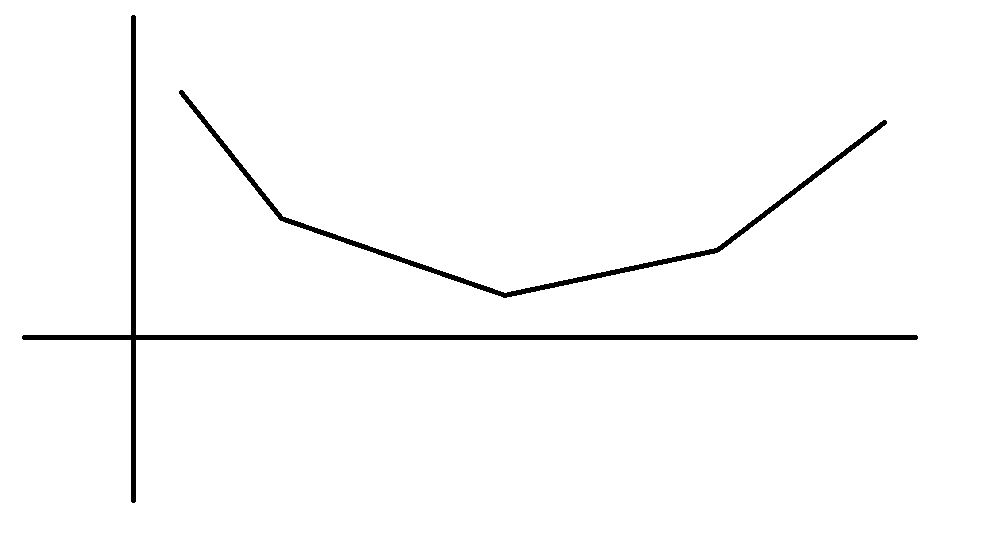
因此我们可以使用队列维护这样一个集合，如果说当前这个点和集合内的最后一个点连起来形成了一个上凸包，那么集合中的最后一个点就可以不要了。因为这个点和集合中的倒数第二个点和最后一个点连起来满足了上凸包的性质，所以中间的那个点（集合中的最后一个点）肯定不会是最优解。

得到这样一个集合过后，我们就要思考什么时候取最小了。根据我们上面提出的两点之间选点的方法，我们很容易得到要找的其实是一个"切点"：

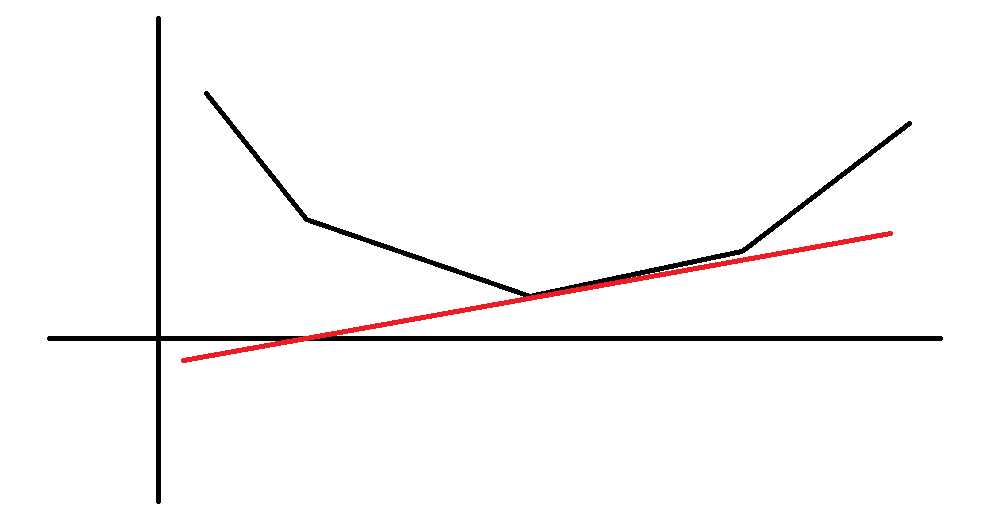
这时，这个点左边的斜率比这条直线斜率小，所以选靠右的点更好，而右边的斜率更大，所以选靠左边的点更好。也就是说：选当前这个点一定是最优的。

我们很容易观察到下凸包的斜率是具有单调性的。所以我们可以选择二分这个点。这样时间复杂度就是 O ( n log ⁡ n ) O(n\log n) O(nlogn)。

于是上面那道题我们就可以非常愉快的解决了。

首先，转移方程是：

f i = min ⁡ j = 0 i − 1 { f j + s t i × ( s f i − s f j ) + s × ( s f n − s f j ) } f_i=\min_{j=0}^{i-1}\{f_j+st_i\times(sf_i-sf_j)+s\times(sf_n-sf_j)\} fi=j=0mini−1{fj+sti×(sfi−sfj)+s×(sfn−sfj)}

拆开，整理一下：

f i = min ⁡ j = 0 i − 1 { f j + s t i × s f i − s t i × s f j + s × s f n − s × s f j } = min ⁡ j = 0 i − 1 { − s t i × s f j + f j − s × s f j } + s t i × s f i + s × s f n \begin{aligned}f_i&=\min_{j=0}^{i-1}\{f_j+st_i\times sf_i-st_i\times sf_j+s\times sf_n-s\times sf_j\}\\&=\min_{j=0}^{i-1}\{-st_i\times sf_j+f_j-s\times sf_j\}+st_i\times sf_i+s\times sf_n\end{aligned} fi=j=0mini−1{fj+sti×sfi−sti×sfj+s×sfn−s×sfj}=j=0mini−1{−sti×sfj+fj−s×sfj}+sti×sfi+s×sfn

再整理成一般形式：

f i − s t i × s f i − s × s f n = min ⁡ j = 0 i − 1 { f j − ( s + s t i ) × s f j } f_i-st_i\times sf_i-s\times sf_n=\min_{j=0}^{i-1}\{f_j-(s+st_i)\times sf_j\} fi−sti×sfi−s×sfn=j=0mini−1{fj−(s+sti)×sfj}

然后我们设 B ( i ) = f i − s t i × s f i − s × s f n , Y ( j ) = f j , K ( i ) = s t i + s , X ( j ) = s f j B(i)=f_i-st_i\times sf_i-s\times sf_n,Y(j)=f_j,K(i)=st_i+s,X(j)=sf_j B(i)=fi−sti×sfi−s×sfn,Y(j)=fj,K(i)=sti+s,X(j)=sfj，于是可以把原方程变成这样：

B ( i ) = min ⁡ j = 0 i − 1 { Y ( j ) − K ( i ) X ( j ) } B(i)=\min_{j=0}^{i-1}\{Y(j)-K(i)X(j)\} B(i)=j=0mini−1{Y(j)−K(i)X(j)}

然后就可以用斜率优化做了。

代码给一份：

#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
code by plh;
namespace fastio
{
	inline int read()
	{
		int z=0,f=1;
		char c=getchar();
		if(c==EOF)
		{
			exit(0);
		}
		while(c<'0'||c>'9')
		{
			if(c=='-')
			{
				f=-1;
			}
			c=getchar();
		}
		while(c>='0'&&c<='9')
		{
			z=z*10+c-'0';
			c=getchar();
		}
		return z*f;
	}
	inline void write(int x)
	{
		if(x<0)
		{
			putchar('-');
			x=-x;
		}
		static int top=0,stk[106];
		while(x)
		{
			stk[++top]=x%10;
			x/=10;
		}
		if(!top)
		{
			stk[++top]=0;
		}
		while(top)
		{
			putchar(char(stk[top--]+'0'));
		}
	}
	inline void write(string s)
	{
		for(auto i:s)
		{
			putchar(i);
		}
	}
}
using namespace fastio;
int n,s,a[300006],b[300006],s1[300006],s2[300006],f[300006],dq[300006];
int search(int x,int y,int z)
{
	int l=x+1,r=y-1,mid,ans=0;
	while(l<=r)
	{
		mid=l+r>>1;
		if((f[dq[mid]]-f[dq[mid-1]])<=(s2[dq[mid]]-s2[dq[mid-1]])*(s+z))
		{
			ans=mid;
			l=mid+1;
		}
		else
		{
			r=mid-1;
		}
	}
	return ans;
}
signed main()
{
	n=read(),s=read();
	for(int i=1;i<=n;i++)
	{
		a[i]=read(),b[i]=read();
		s1[i]=s1[i-1]+a[i];
		s2[i]=s2[i-1]+b[i];
	}
	int l=1,r=1;
	f[0]=0;
	dq[r]=0;
	r++;
	for(int i=1;i<=n;i++)
	{
		int it=search(l,r,s1[i]);
		f[i]=f[dq[it]]-(s+s1[i])*s2[dq[it]]+s1[i]*s2[i]+s*s2[n];
		while(l<r-1&&(f[dq[r-1]]-f[dq[r-2]])*(s2[i]-s2[dq[r-1]])>=(s2[dq[r-1]]-s2[dq[r-2]])*(f[i]-f[dq[r-1]]))
		//队列里面最后一定要留一个点
		{
			r--;
		}
		dq[r]=i;
		r++;
	}
	write(f[n]);
	return 0;
}

当然，这是一般情况，不过我们还有特殊情况。

当斜率单调递增时

如果说我们每次的 K ( i ) K(i) K(i) 时单调递增的，那么我们不难发现：我们每次选的点一定不在上一次选的点的左边。换句话说：我们选的点一定会一直往右移动。这启发了我们可以用单调队列。

我们每次比较时，如果当前这条边的斜率比 K ( i ) K(i) K(i) 要小，那这条边肯定不可能用。而因为斜率在持续增大，所以我们每次选的点一定会向右移动。那么之前弹出去的点我们就不会再用。而且这里涉及到求最值，符合单调队列优化的使用情况。

附代码：

#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
code by plh;
namespace fastio
{
	inline int read()
	{
		int z=0,f=1;
		char c=getchar();
		if(c==EOF)
		{
			exit(0);
		}
		while(c<'0'||c>'9')
		{
			if(c=='-')
			{
				f=-1;
			}
			c=getchar();
		}
		while(c>='0'&&c<='9')
		{
			z=z*10+c-'0';
			c=getchar();
		}
		return z*f;
	}
	inline void write(int x)
	{
		if(x<0)
		{
			putchar('-');
			x=-x;
		}
		static int top=0,stk[106];
		while(x)
		{
			stk[++top]=x%10;
			x/=10;
		}
		if(!top)
		{
			stk[++top]=0;
		}
		while(top)
		{
			putchar(char(stk[top--]+'0'));
		}
	}
	inline void write(string s)
	{
		for(auto i:s)
		{
			putchar(i);
		}
	}
}
using namespace fastio;
int n,s,l=1,r=1,a[300006],b[300006],s1[300006],s2[300006],f[300006],dq[300006];
signed main()
{
	n=read(),s=read();
	for(int i=1;i<=n;i++)
	{
		a[i]=read(),b[i]=read();
		s1[i]=s1[i-1]+a[i];
		s2[i]=s2[i-1]+b[i];
	}
	f[0]=0;
	dq[r]=0;
	r++;
	for(int i=1;i<=n;i++)
	{
		while(l<r-1&&(f[dq[l+1]]-f[dq[l]])<=(s2[dq[l+1]]-s2[dq[l]])*(s+s1[i]))
		//比较斜率这里也可以写除法，不过要考虑精度问题
		{
			l++;
		}
		f[i]=f[dq[l]]-(s+s1[i])*s2[dq[l]]+s1[i]*s2[i]+s*s2[n];
		while(l<r-1&&(f[dq[r-1]]-f[dq[r-2]])*(s2[i]-s2[dq[r-1]])>=(s2[dq[r-1]]-s2[dq[r-2]])*(f[i]-f[dq[r-1]]))
		{
			r--;
		}
		dq[r]=i;
		r++;
	}
	write(f[n]);
	return 0;
}