目录
[1. 缘起:最大似然估计 (MLE)](#1. 缘起:最大似然估计 (MLE))
[2. 困境:当数据变得"暧昧"](#2. 困境:当数据变得“暧昧”)
[3. 直观破解:投硬币的智慧](#3. 直观破解:投硬币的智慧)
[4. 深入骨髓:数学推导与 Jensen 不等式](#4. 深入骨髓:数学推导与 Jensen 不等式)
[神器:Jensen 不等式](#神器:Jensen 不等式)
[EM 的本质](#EM 的本质)
[5. 算法流程总结](#5. 算法流程总结)
[6. 应用:高斯混合模型 (GMM)](#6. 应用:高斯混合模型 (GMM))
在机器学习的江湖中,有一类问题特别让人头疼:"缺斤少两"。
通常我们做参数估计(比如最大似然估计),前提是数据是完整的。但如果数据里含有我们看不见的"隐变量"(Latent Variable),传统的办法就失灵了。这时候,就轮到 EM 算法(期望最大化算法) 出场了。它像是一个聪明的策略家,在信息不全的情况下,通过一步步"猜测-修正",最终找到最优解。
今天,我们就结合生动的例子和严谨的数学推导,来彻底搞懂 EM 算法。
1. 缘起:最大似然估计 (MLE)
在讲 EM 之前,我们先回顾一下它的基础------最大似然估计。
举个栗子:
你走进一家赌场,不知道这家的胜率如何。你在门口蹲守,观察了5个人出来,结果这5个人都说自己"赚了"。基于这个观测结果,作为理性人的你会怎么推断?你会认为这家赌场赚钱的概率非常大。
这就是最大似然的核心思想:调整模型的参数,使得出现当前观测样本的概率最大化。
如果用数学语言描述:
假设我们要调查100名男生的身高分布。我们假设身高服从高斯分布(正态分布)。只要我们手握这100个数据,直接求均值和方差,就能得到这个高斯分布的参数。这很简单,因为样本是独立同分布的。
2. 困境:当数据变得"暧昧"
现在,问题升级了。
这100个身高数据里,不仅仅有男生,还有女生。
-
男生服从一个高斯分布(高个子)。
-
女生服从另一个高斯分布(矮个子)。
-
最要命的是:我们只知道身高数值,却不知道哪个数据是男生的,哪个是女生的。
这里的"性别",就是我们看不见的隐变量 (Latent Variable) ,通常记为 。
如果我们知道性别,直接把男女分开,分别求平均值就好了。
如果我们知道男女分布的参数(均值方差),我们也能算出某个人大概率是男是女。
死循环出现了: 要算参数得先知道性别,要知道性别得先有参数。这就变成了"鸡生蛋,蛋生鸡"的问题。
3. 直观破解:投硬币的智慧
为了打破这个死循环,我们来看一个经典的投硬币例子。
场景:
我们要估计 A、B 两枚硬币正面朝上的概率。我们做了5组实验,每组投10次。
-
情况一(简单模式):我们知道每一组是用哪个硬币投的。那太简单了,直接数数,算比例就行。
-
情况二(困难模式):我们只有投掷结果(比如"5正5反"),但不知道这一组是用 A 投的还是 B 投的。
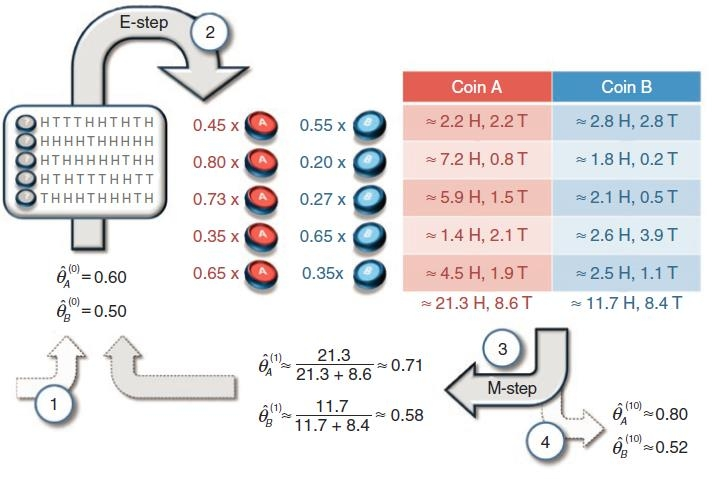
EM 算法是这样解决困难模式的:
-
初始化:先瞎猜一个 A 和 B 的初始概率(比如猜 A 是 0.6,B 是 0.5)。
-
E-step (期望步):基于目前的猜测,去"反推"每一组实验数据更像是 A 产生的,还是 B 产生的。
-
比如第一组数据是"5正5反"。通过计算,发现如果是 A 投的概率较小,如果是 B 投的概率较大。
-
我们不直接说它"肯定"是 B,而是给它分配一个权重(比如 0.45 属于 A,0.55 属于 B)。
-
-
M-step (最大化步):根据刚才算出来的权重(也就是"补全"了数据),重新计算 A 和 B 的真实概率。
-
循环:用新的概率再去推测权重,周而复始,直到参数不再变化。
4. 深入骨髓:数学推导与 Jensen 不等式
为什么刚才那个"瞎猜-修正"的方法一定能收敛到正确结果?这就需要数学来背书了。
面对含有隐变量 的似然函数,我们需要优化的目标是:
难点在于:log 里面有个 sum (求和)。这在数学上极难求导。
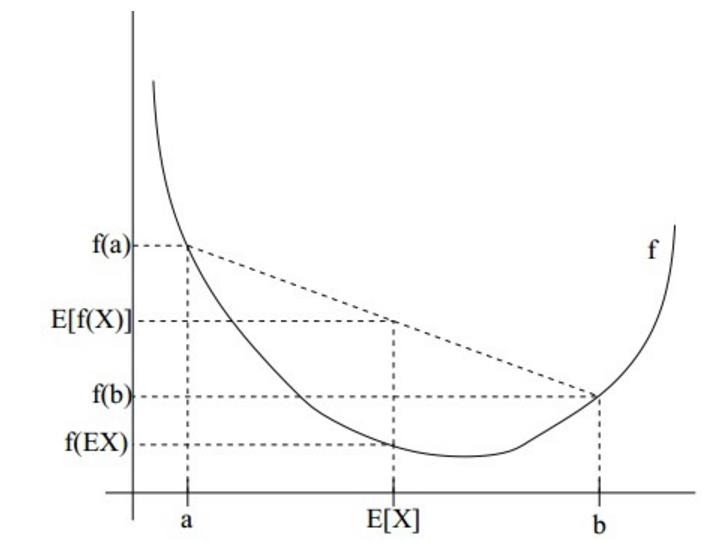
神器:Jensen 不等式
为了解决 log-sum 问题,我们引入了一个辅助分布,把公式强行变换:
利用 Jensen 不等式(对于凹函数 log,),我们可以找到目标函数的一个下界 (Lower Bound):
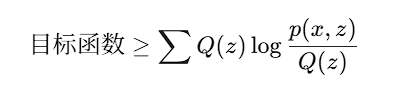
EM 的本质
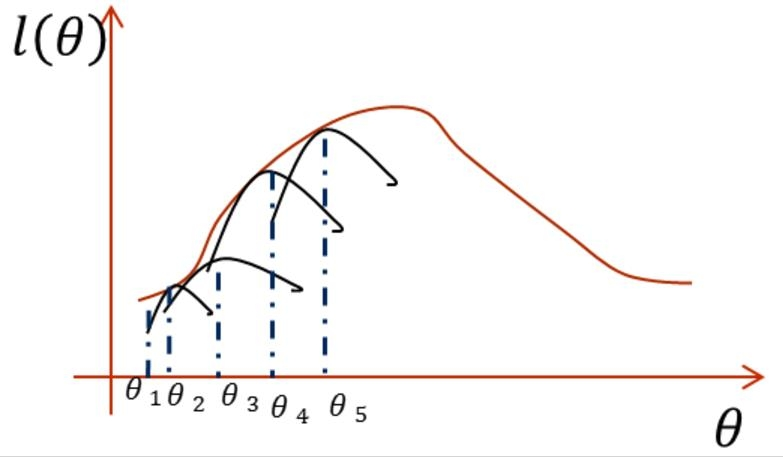
EM 算法的本质,就是通过不断提升这个下界,来逼近目标函数的最大值。
-
E步 :固定参数
,调整
,让下界紧紧顶住目标函数(使等号成立)。推导发现,这个最优的
其实就是后验概率
。
-
M步 :固定
,调整参数
,让这个下界函数达到最高点。
5. 算法流程总结
经过数学推导,我们终于得到了通用的 EM 算法流程:
-
初始化 :随机选择分布参数
的初值。
-
E-step (填坑):
计算每个样本属于隐变量类别
的概率(即后验概率
)。
-
M-step (优化):
根据计算出的
,最大化似然函数的下界,求解出新的参数
。
-
迭代:重复步骤 2 和 3,直到收敛。
6. 应用:高斯混合模型 (GMM)
EM 算法最著名的应用就是 GMM (Gaussian Mixture Model)。
正如文章开头提到的身高问题,GMM 认为数据是由 个高斯分布混合而成的。EM 算法在 GMM 中:
-
E步 :计算每个数据点属于第
个高斯分布的概率(软聚类)。
-
M步:根据这些概率,重新计算每个高斯分布的均值和方差。
这听起来是不是很像 K-Means 聚类?没错,K-Means 其实是 GMM 的一种特例(硬聚类)。
结语
EM 算法是统计学习中一颗璀璨的明珠。它告诉我们:面对未知和残缺,不要试图一步到位。先给出一个假设,再去验证和修正,在不断的迭代中,真相自然会浮出水面。