【强化学习】DQN 改进算法

目录

一、引言

[二、Double DQN 算法](#二、Double DQN 算法)

[（一）Double DQN 的提出背景：解决原始 DQN 的 Q 值过估计问题](#（一）Double DQN 的提出背景：解决原始 DQN 的 Q 值过估计问题)

[原始 DQN 的目标 Q 值计算逻辑](#原始 DQN 的目标 Q 值计算逻辑)

[（二）Double DQN 的核心思想："选动作" 和 "评价值" 解耦](#（二）Double DQN 的核心思想：“选动作” 和 “评价值” 解耦)

[Double DQN 的目标 Q 值计算逻辑](#Double DQN 的目标 Q 值计算逻辑)

[（三）Double DQN 与原始 DQN 的核心对比](#（三）Double DQN 与原始 DQN 的核心对比)

[1. 原始 DQN 的实现（代码片段）](#1. 原始 DQN 的实现（代码片段）)

[2. Double DQN 的实现（代码片段）](#2. Double DQN 的实现（代码片段）)

[（四）Double DQN 的完整执行流程](#（四）Double DQN 的完整执行流程)

[（五）Double DQN 的Python代码完整实现](#（五）Double DQN 的Python代码完整实现)

（六）程序运行结果展示与分析

结果展示

结果分析

[（七）Double DQN 的优势与适用场景](#（七）Double DQN 的优势与适用场景)

优势

适用场景

（八）关键总结

[三、Dueling DQN 算法](#三、Dueling DQN 算法)

[（一）Dueling DQN 的提出背景：优化 Q 值的学习结构](#（一）Dueling DQN 的提出背景：优化 Q 值的学习结构)

[（二）Dueling DQN 的核心思想：拆分 Q 值为 V (s) 和 A (s,a)](#（二）Dueling DQN 的核心思想：拆分 Q 值为 V (s) 和 A (s,a))

[1. 核心公式：Q 值的拆解与重构](#1. 核心公式：Q 值的拆解与重构)

[2. 关键改进：解决 "不可识别性" 问题](#2. 关键改进：解决 “不可识别性” 问题)

[（三）Dueling DQN 的网络结构](#（三）Dueling DQN 的网络结构)

[1. 原始 DQN 的 Qnet（单层隐藏层）](#1. 原始 DQN 的 Qnet（单层隐藏层）)

[2. Dueling DQN 的 VAnet（拆分 V 和 A）](#2. Dueling DQN 的 VAnet（拆分 V 和 A）)

[（四）Dueling DQN 的训练逻辑（和原始 DQN 的异同）](#（四）Dueling DQN 的训练逻辑（和原始 DQN 的异同）)

[1. 初始化时的网络选择](#1. 初始化时的网络选择)

[2. 训练 / 更新逻辑](#2. 训练 / 更新逻辑)

[（五）Dueling DQN 的Python代码完整实现](#（五）Dueling DQN 的Python代码完整实现)

（六）程序运行结果展示与分析

结果展示

结果分析

[（七）Dueling DQN 的优势与适用场景](#（七）Dueling DQN 的优势与适用场景)

核心优势

适用场景

[（八）Dueling DQN vs Double DQN：核心区别](#（八）Dueling DQN vs Double DQN：核心区别)

（九）关键总结

四、总结

---

一、引言

DQN 算法敲开了深度强化学习的大门，但是作为先驱性的工作，其本身存在着一些问题以及一些可以改进的地方。于是，在 DQN 之后，学术界涌现出了非常多的改进算法。本文将介绍其中两个非常著名的算法：Double DQN 和 Dueling DQN，这两个算法的实现非常简单，只需要在 DQN 的基础上稍加修改，它们能在一定程度上改善 DQN 的效果。

二、Double DQN 算法

（一）Double DQN 的提出背景：解决原始 DQN 的 Q 值过估计问题

在学习 Double DQN 之前，首先要明白原始 DQN 的核心缺陷 ------Q 值过估计（Overestimation）：原始 DQN 计算目标 Q 值时，存在一个关键问题：用同一个目标网络（target_q_net）既选择 "最优动作"，又评估这个动作的 Q 值。

原始 DQN 的目标 Q 值计算逻辑

原始 DQN 的目标 Q 值公式为：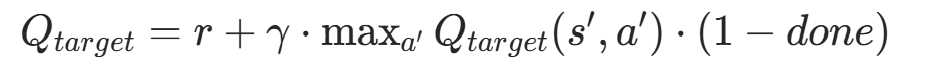

• r：当前步的奖励
• γ：折扣因子
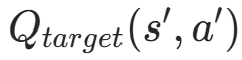• ：目标网络对下一状态s′下动作a′的 Q 值估计
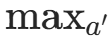• ：取目标网络中下一状态的最大 Q 值对应的动作
• done：是否到达终止状态

问题根源 ：Q 网络的输出本身存在估计误差（比如噪声、训练不充分），而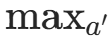这个 "最大化操作" 会放大这种误差，导致目标 Q 值被系统性高估。这种过估计会让智能体学习到错误的价值信号，最终影响策略的收敛效果。

（二）Double DQN 的核心思想："选动作" 和 "评价值" 解耦

Double DQN 的核心改进非常简洁：

将 "选择最优动作" 和 "评估该动作的 Q 值" 拆分成两个独立的步骤，用当前 Q 网络（q_net）选动作 ，用目标 Q 网络（target_q_net）评价值，避免同一网络的误差被最大化操作放大。

Double DQN 的目标 Q 值计算逻辑

分为两步：

1. 选动作 ：用当前 Q 网络（q_net）找到下一状态s′下 Q 值最大的动作：
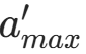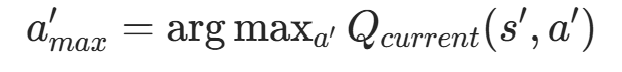
2. 评价值 ：用目标 Q 网络（target_q_net）计算该动作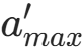的 Q 值：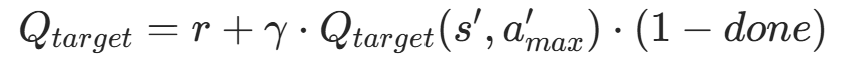

这种 "分离" 的设计，能有效降低最大化操作带来的误差放大，从而缓解 Q 值过估计问题。

（三）Double DQN 与原始 DQN 的核心对比

DQN类的update函数是区分两种算法的核心，我把关键代码和原理对应起来，进行讲解：

1. 原始 DQN 的实现（代码片段）

else:  # DQN的情况
    max_next_q_values = self.target_q_net(next_states).max(1)[0].view(-1, 1)

• 逻辑：直接从target_q_net（目标网络）中取下一状态的最大 Q 值，对应公式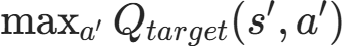
• 问题：目标网络既选动作，又评价值，放大误差。

2. Double DQN 的实现（代码片段）

if self.dqn_type == 'DoubleDQN':  # DQN与Double DQN的区别
    max_action = self.q_net(next_states).max(1)[1].view(-1, 1)  # 步骤1：当前网络选动作
    max_next_q_values = self.target_q_net(next_states).gather(1, max_action)  # 步骤2：目标网络评价值

• self.q_net(next_states).max(1)[1]：当前网络（q_net）计算下一状态的所有动作 Q 值，取最大 Q 值对应的动作索引（argmax）；
• target_q_net(...).gather(1, max_action)：目标网络（target_q_net）根据当前网络选的动作索引，计算该动作的 Q 值（而非直接取最大值）；
• 优势：选动作和评价值的网络分离，避免误差放大。

（四）Double DQN 的完整执行流程

Double DQN 的完整训练流程如下：

1. 环境交互 ：智能体通过take_action函数选择动作（ε- 贪心策略），与环境交互得到(s,a,r,s′,done)；
2. 经验存储 ：将交互数据存入经验回放池ReplayBuffer；
3. 批量采样：当回放池数据量足够时，采样一批数据；
4. 更新网络 ：
   • 计算当前 Q 值：（当前网络对 "状态 s 下选动作 a" 的 Q 值）；
   • 计算目标 Q 值：按 Double DQN 逻辑计算；
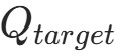   • 损失计算：MSE 损失（）；
   • 梯度下降：更新当前网络参数，每隔target_update步同步到目标网络；
5. 循环迭代：重复上述步骤，直到训练结束。

（五）Double DQN 的Python代码完整实现

先实现rl_utils库，它包含一些函数，如绘制移动平均曲线、计算优势函数等，不同的算法可以一起使用这些函数。

rl_utils.py中的Python代码如下：

from tqdm import tqdm
import numpy as np
import torch
import collections
import random
 
class ReplayBuffer:
    def __init__(self, capacity):
        self.buffer = collections.deque(maxlen=capacity) 
 
    def add(self, state, action, reward, next_state, done): 
        self.buffer.append((state, action, reward, next_state, done)) 
 
    def sample(self, batch_size): 
        transitions = random.sample(self.buffer, batch_size)
        state, action, reward, next_state, done = zip(*transitions)
        return np.array(state), action, reward, np.array(next_state), done 
 
    def size(self): 
        return len(self.buffer)
 
def moving_average(a, window_size):
    cumulative_sum = np.cumsum(np.insert(a, 0, 0)) 
    middle = (cumulative_sum[window_size:] - cumulative_sum[:-window_size]) / window_size
    r = np.arange(1, window_size-1, 2)
    begin = np.cumsum(a[:window_size-1])[::2] / r
    end = (np.cumsum(a[:-window_size:-1])[::2] / r)[::-1]
    return np.concatenate((begin, middle, end))
 
def train_on_policy_agent(env, agent, num_episodes):
    return_list = []
    for i in range(10):
        with tqdm(total=int(num_episodes/10), desc='Iteration %d' % i) as pbar:
            for i_episode in range(int(num_episodes/10)):
                episode_return = 0
                transition_dict = {'states': [], 'actions': [], 'next_states': [], 'rewards': [], 'dones': []}
                state = env.reset()
                done = False
                while not done:
                    action = agent.take_action(state)
                    next_state, reward, done, _ = env.step(action)
                    transition_dict['states'].append(state)
                    transition_dict['actions'].append(action)
                    transition_dict['next_states'].append(next_state)
                    transition_dict['rewards'].append(reward)
                    transition_dict['dones'].append(done)
                    state = next_state
                    episode_return += reward
                return_list.append(episode_return)
                agent.update(transition_dict)
                if (i_episode+1) % 10 == 0:
                    pbar.set_postfix({'episode': '%d' % (num_episodes/10 * i + i_episode+1), 'return': '%.3f' % np.mean(return_list[-10:])})
                pbar.update(1)
    return return_list
 
def train_off_policy_agent(env, agent, num_episodes, replay_buffer, minimal_size, batch_size):
    return_list = []
    for i in range(10):
        with tqdm(total=int(num_episodes/10), desc='Iteration %d' % i) as pbar:
            for i_episode in range(int(num_episodes/10)):
                episode_return = 0
                state = env.reset()
                done = False
                while not done:
                    action = agent.take_action(state)
                    next_state, reward, done, _ = env.step(action)
                    replay_buffer.add(state, action, reward, next_state, done)
                    state = next_state
                    episode_return += reward
                    if replay_buffer.size() > minimal_size:
                        b_s, b_a, b_r, b_ns, b_d = replay_buffer.sample(batch_size)
                        transition_dict = {'states': b_s, 'actions': b_a, 'next_states': b_ns, 'rewards': b_r, 'dones': b_d}
                        agent.update(transition_dict)
                return_list.append(episode_return)
                if (i_episode+1) % 10 == 0:
                    pbar.set_postfix({'episode': '%d' % (num_episodes/10 * i + i_episode+1), 'return': '%.3f' % np.mean(return_list[-10:])})
                pbar.update(1)
    return return_list
 
 
def compute_advantage(gamma, lmbda, td_delta):
    td_delta = td_delta.detach().numpy()
    advantage_list = []
    advantage = 0.0
    for delta in td_delta[::-1]:
        advantage = gamma * lmbda * advantage + delta
        advantage_list.append(advantage)
    advantage_list.reverse()
    return torch.tensor(advantage_list, dtype=torch.float)

Double DQN 的Python代码如下：

import collections
import random
import gymnasium as gym
import numpy as np
import torch
import torch.nn.functional as F
import matplotlib.pyplot as plt
from tqdm import tqdm


class ReplayBuffer:
    '''经验回放池'''
    def __init__(self, capacity):
        self.buffer = collections.deque(maxlen=capacity)     # 队列，先进先出

    def add(self, state, action, reward, next_state, done):   # 将数据加入buffer
        self.buffer.append((state, action, reward, next_state, done))

    def sample(self, batch_size):      # 从buffer中采样数据，数量为batch_size
        transitions = random.sample(self.buffer, batch_size)
        state, action, reward, next_state, done = zip(*transitions)
        return np.array(state), action, reward, np.array(next_state), done

    def size(self):         # 目前buffer中数据的数量
        return len(self.buffer)

def moving_average(a, window_size):
    '''滑动平均函数'''
    cumulative_sum = np.cumsum(np.insert(a, 0, 0))
    middle = (cumulative_sum[window_size:] - cumulative_sum[:-window_size]) / window_size
    r = np.arange(1, window_size-1, 2)
    begin = np.cumsum(a[:window_size-1])[::2] / r
    end = (np.cumsum(a[:-window_size:-1])[::2] / r)[::-1]
    return np.concatenate((begin, middle, end))

# 定义一个只有一层隐藏层的Q网络
class Qnet(torch.nn.Module):
    '''只有一层隐藏层的Q网络'''
    def __init__(self, state_dim, hidden_dim, action_dim):
        super(Qnet, self).__init__()
        self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
        self.fc2 = torch.nn.Linear(hidden_dim, action_dim)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        return self.fc2(x)

# Double DQN算法
class DQN:
    '''DQN算法，包括Double DQN'''
    def __init__(self, state_dim, hidden_dim, action_dim, learning_rate, gamma, epsilon, target_update, device, dqn_type='VanillaDQN'):
        self.action_dim = action_dim
        self.q_net = Qnet(state_dim, hidden_dim, self.action_dim).to(device)
        self.target_q_net = Qnet(state_dim, hidden_dim, self.action_dim).to(device)
        self.optimizer = torch.optim.Adam(self.q_net.parameters(), lr=learning_rate)
        self.gamma = gamma
        self.epsilon = epsilon
        self.target_update = target_update
        self.count = 0
        self.dqn_type = dqn_type
        self.device = device

    def take_action(self, state):
        if np.random.random() < self.epsilon:
            action = np.random.randint(self.action_dim)
        else:
            # 优化张量创建：先转numpy数组再创建张量，避免警告
            state = torch.tensor(np.array([state]), dtype=torch.float32).to(self.device)
            action = self.q_net(state).argmax().item()
        return action

    def max_q_value(self, state):
        # 优化张量创建
        state = torch.tensor(np.array([state]), dtype=torch.float32).to(self.device)
        return self.q_net(state).max().item()

    def update(self, transition_dict):
        states = torch.tensor(transition_dict['states'], dtype=torch.float32).to(self.device)
        actions = torch.tensor(transition_dict['actions']).view(-1, 1).to(self.device)
        rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float32).view(-1, 1).to(self.device)
        next_states = torch.tensor(transition_dict['next_states'], dtype=torch.float32).to(self.device)
        dones = torch.tensor(transition_dict['dones'], dtype=torch.float32).view(-1, 1).to(self.device)

        q_values = self.q_net(states).gather(1, actions)
        if self.dqn_type == 'DoubleDQN':      # DQN与Double DQN的区别
            max_action = self.q_net(next_states).max(1)[1].view(-1, 1)
            max_next_q_values = self.target_q_net(next_states).gather(1, max_action)
        else:       # DQN的情况
            max_next_q_values = self.target_q_net(next_states).max(1)[0].view(-1, 1)
        q_targets = rewards + self.gamma * max_next_q_values * (1 - dones)
        dqn_loss = torch.mean(F.mse_loss(q_values, q_targets))
        self.optimizer.zero_grad()
        dqn_loss.backward()
        self.optimizer.step()

        if self.count % self.target_update == 0:
            self.target_q_net.load_state_dict(self.q_net.state_dict())
        self.count += 1

# 设置超参数
lr = 1e-2
num_episodes = 200
hidden_dim = 128
gamma = 0.98
epsilon = 0.01
target_update = 50
buffer_size = 5000
minimal_size = 1000
batch_size = 64
device = torch.device("cuda") if torch.cuda.is_available() else torch.device("cpu")

env_name = 'Pendulum-v1'
env = gym.make(env_name)
state_dim = env.observation_space.shape[0]
action_dim = 11        # 将连续动作分成11个离散动作

def dis_to_con(discrete_action, env, action_dim):      # 离散动作转回连续的函数
    action_lowbound = env.action_space.low[0]    # 连续动作的最小值
    action_upbound = env.action_space.high[0]    # 连续动作的最大值
    return action_lowbound + (discrete_action / (action_dim - 1)) * (action_upbound - action_lowbound)

# 对比DQN和Double DQN的训练情况
def train_DQN(agent, env, num_episodes, replay_buffer, minimal_size, batch_size):
    return_list = []
    max_q_value_list = []
    max_q_value = 0
    for i in range(10):
        with tqdm(total=int(num_episodes / 10), desc='Iteration %d' % i) as pbar:
            for i_episode in range(int(num_episodes / 10)):
                episode_return = 0
                state, _ = env.reset()  # gymnasium的reset返回(state, info)
                done = False
                while not done:
                    action = agent.take_action(state)
                    max_q_value = agent.max_q_value(state) * 0.005 + max_q_value * 0.995  # 平滑处理
                    max_q_value_list.append(max_q_value)   # 保存每个状态的最大Q值
                    action_continuous = dis_to_con(action, env, agent.action_dim)
                    # gymnasium的step返回(next_state, reward, terminated, truncated, info)
                    next_state, reward, terminated, truncated, _ = env.step([action_continuous])
                    done = terminated or truncated  # 合并终止条件
                    replay_buffer.add(state, action, reward, next_state, done)
                    state = next_state
                    episode_return += reward
                    if replay_buffer.size() > minimal_size:
                        b_s, b_a, b_r, b_ns, b_d = replay_buffer.sample(batch_size)
                        transition_dict = {
                            'states': b_s,
                            'actions': b_a,
                            'next_states': b_ns,
                            'rewards': b_r,
                            'dones': b_d
                        }
                        agent.update(transition_dict)
                return_list.append(episode_return)
                if (i_episode + 1) % 10 == 0:
                    pbar.set_postfix({
                        'episode': '%d' % (num_episodes / 10 * i + i_episode + 1),
                        'return': '%.3f' % np.mean(return_list[-10:])
                    })
                pbar.update(1)
    return return_list, max_q_value_list

# 训练DQN并打印出其学习过程中最大Q值的情况
random.seed(0)
np.random.seed(0)
torch.manual_seed(0)
replay_buffer = ReplayBuffer(buffer_size)
agent = DQN(state_dim, hidden_dim, action_dim, lr, gamma, epsilon, target_update, device)
return_list, max_q_value_list = train_DQN(agent, env, num_episodes, replay_buffer, minimal_size, batch_size)

episodes_list = list(range(len(return_list)))
mv_return = moving_average(return_list, 5)
plt.plot(episodes_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('DQN on {}'.format(env_name))
plt.savefig('DQN_Pendulum_returns.png', dpi=300, bbox_inches='tight')  # 保存DQN回报图
plt.show()

frames_list = list(range(len(max_q_value_list)))
plt.plot(frames_list, max_q_value_list)
plt.axhline(0, c='orange', ls='--')
plt.axhline(10, c='red', ls='--')
plt.xlabel('Frames')
plt.ylabel('Q value')
plt.title('DQN on {}'.format(env_name))
plt.savefig('DQN_Pendulum_q_value.png', dpi=300, bbox_inches='tight')  # 保存DQN Q值图
plt.show()

# 训练Double DQN并打印出其学习过程中最大Q值的情况
random.seed(0)
np.random.seed(0)
torch.manual_seed(0)
replay_buffer = ReplayBuffer(buffer_size)
agent = DQN(state_dim, hidden_dim, action_dim, lr, gamma, epsilon, target_update, device, 'DoubleDQN')
return_list, max_q_value_list = train_DQN(agent, env, num_episodes, replay_buffer, minimal_size, batch_size)

episodes_list = list(range(len(return_list)))
mv_return = moving_average(return_list, 5)
plt.plot(episodes_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('Double DQN on {}'.format(env_name))
plt.savefig('DoubleDQN_Pendulum_returns.png', dpi=300, bbox_inches='tight')  # 保存Double DQN回报图
plt.show()

frames_list = list(range(len(max_q_value_list)))
plt.plot(frames_list, max_q_value_list)
plt.axhline(0, c='orange', ls='--')
plt.axhline(10, c='red', ls='--')
plt.xlabel('Frames')
plt.ylabel('Q value')
plt.title('Double DQN on {}'.format(env_name))
plt.savefig('DoubleDQN_Pendulum_q_value.png', dpi=300, bbox_inches='tight')  # 保存Double DQN Q值图
plt.show()

（六）程序运行结果展示与分析

结果展示

Iteration 0: 100%|██████████| 20/20 [00:03<00:00, 5.42it/s, episode=20, return=-875.812]

Iteration 1: 100%|██████████| 20/20 [00:04<00:00, 4.07it/s, episode=40, return=-379.346]

Iteration 2: 100%|██████████| 20/20 [00:05<00:00, 3.96it/s, episode=60, return=-174.580]

Iteration 3: 100%|██████████| 20/20 [00:05<00:00, 3.91it/s, episode=80, return=-320.419]

Iteration 4: 100%|██████████| 20/20 [00:05<00:00, 3.86it/s, episode=100, return=-212.289]

Iteration 5: 100%|██████████| 20/20 [00:05<00:00, 3.74it/s, episode=120, return=-331.470]

Iteration 6: 100%|██████████| 20/20 [00:05<00:00, 3.52it/s, episode=140, return=-271.371]

Iteration 7: 100%|██████████| 20/20 [00:05<00:00, 3.69it/s, episode=160, return=-188.345]

Iteration 8: 100%|██████████| 20/20 [00:05<00:00, 3.45it/s, episode=180, return=-284.761]

Iteration 9: 100%|██████████| 20/20 [00:05<00:00, 3.48it/s, episode=200, return=-163.872]

Iteration 0: 100%|██████████| 20/20 [00:04<00:00, 4.98it/s, episode=20, return=-874.503]

Iteration 1: 100%|██████████| 20/20 [00:05<00:00, 3.76it/s, episode=40, return=-273.172]

Iteration 2: 100%|██████████| 20/20 [00:05<00:00, 3.82it/s, episode=60, return=-305.257]

Iteration 3: 100%|██████████| 20/20 [00:05<00:00, 3.74it/s, episode=80, return=-184.016]

Iteration 4: 100%|██████████| 20/20 [00:05<00:00, 3.60it/s, episode=100, return=-217.799]

Iteration 5: 100%|██████████| 20/20 [00:05<00:00, 3.45it/s, episode=120, return=-201.688]

Iteration 6: 100%|██████████| 20/20 [00:05<00:00, 3.47it/s, episode=140, return=-250.269]

Iteration 7: 100%|██████████| 20/20 [00:05<00:00, 3.40it/s, episode=160, return=-245.639]

Iteration 8: 100%|██████████| 20/20 [00:06<00:00, 3.26it/s, episode=180, return=-137.447]

Iteration 9: 100%|██████████| 20/20 [00:06<00:00, 3.22it/s, episode=200, return=-202.928]

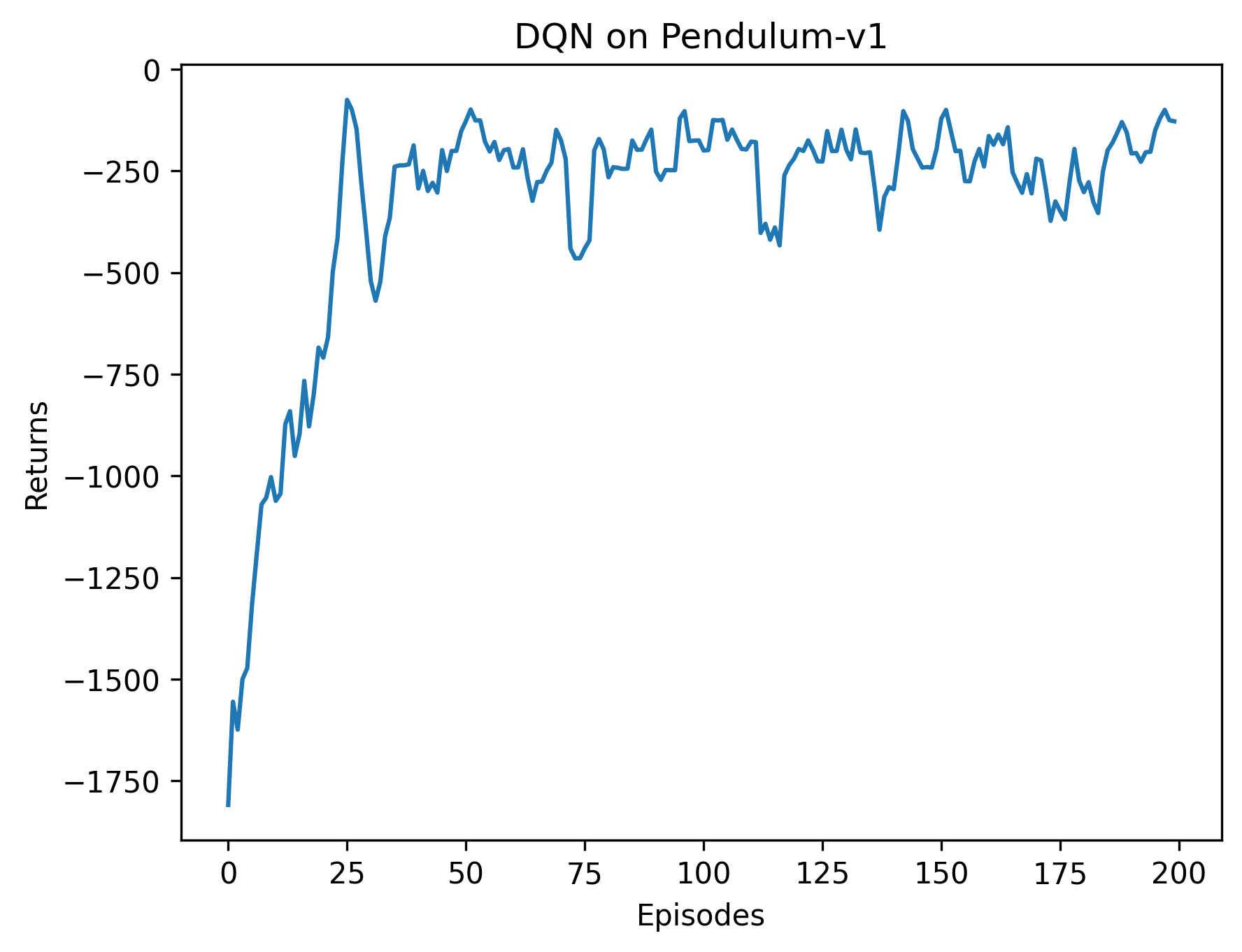
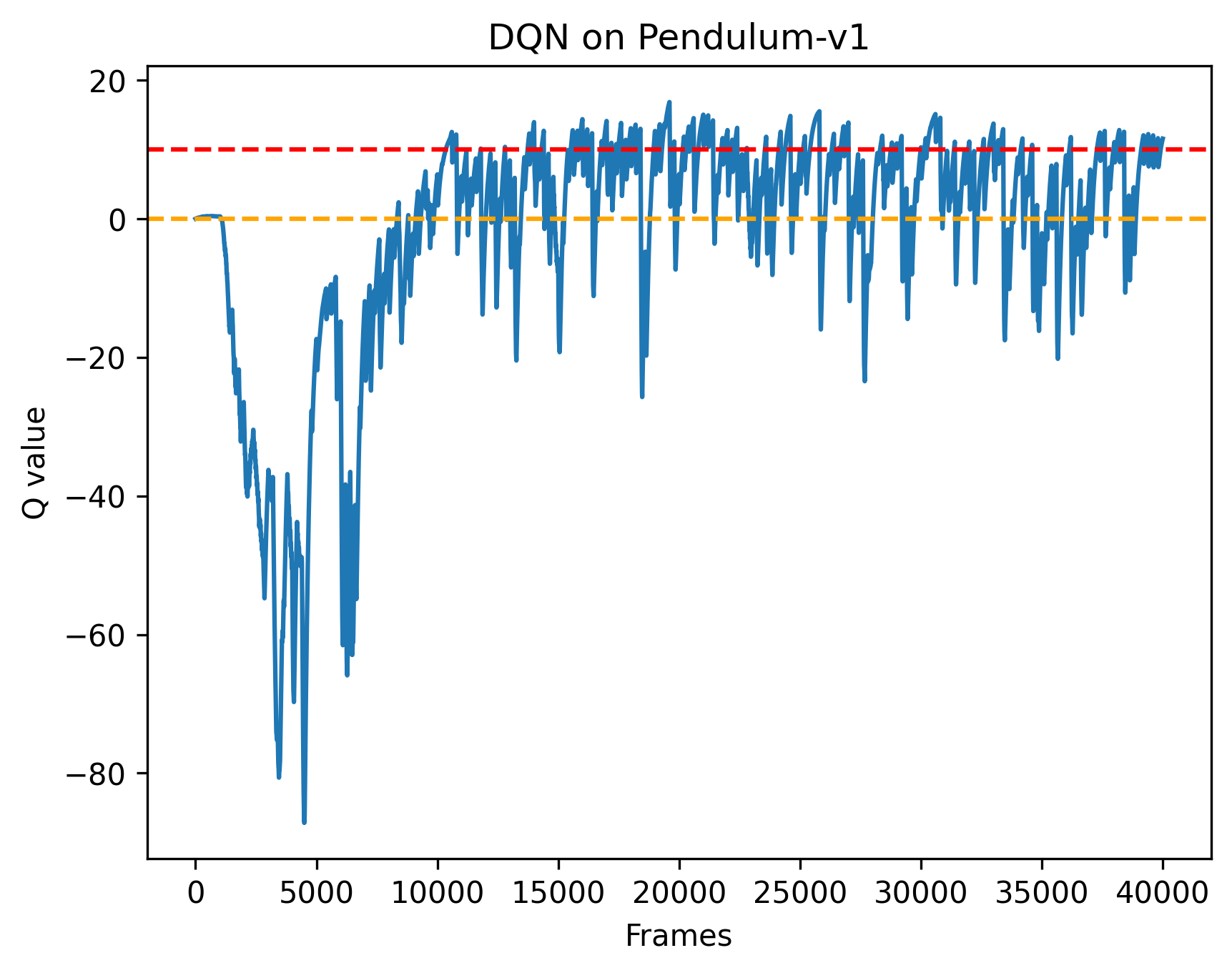
结果分析

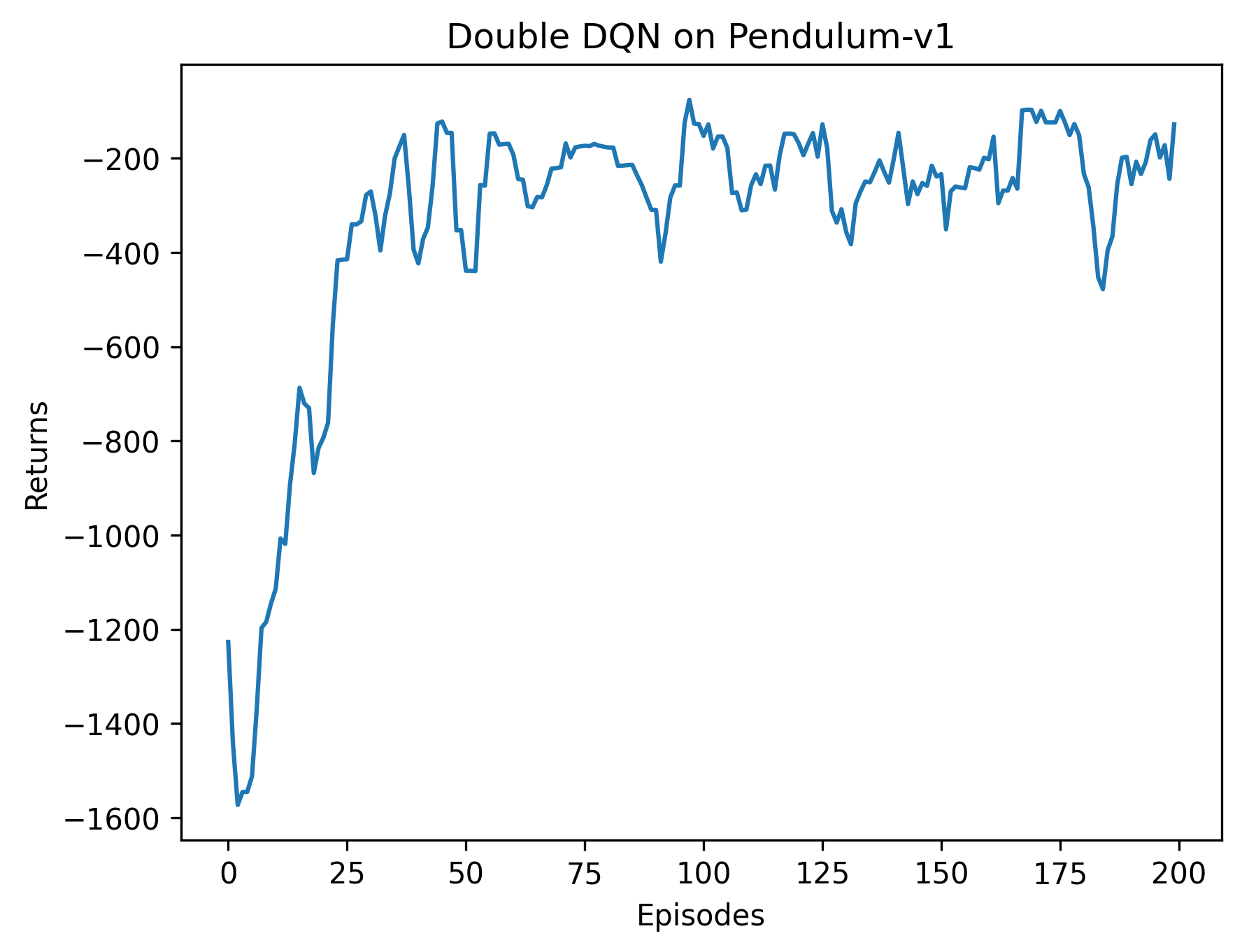
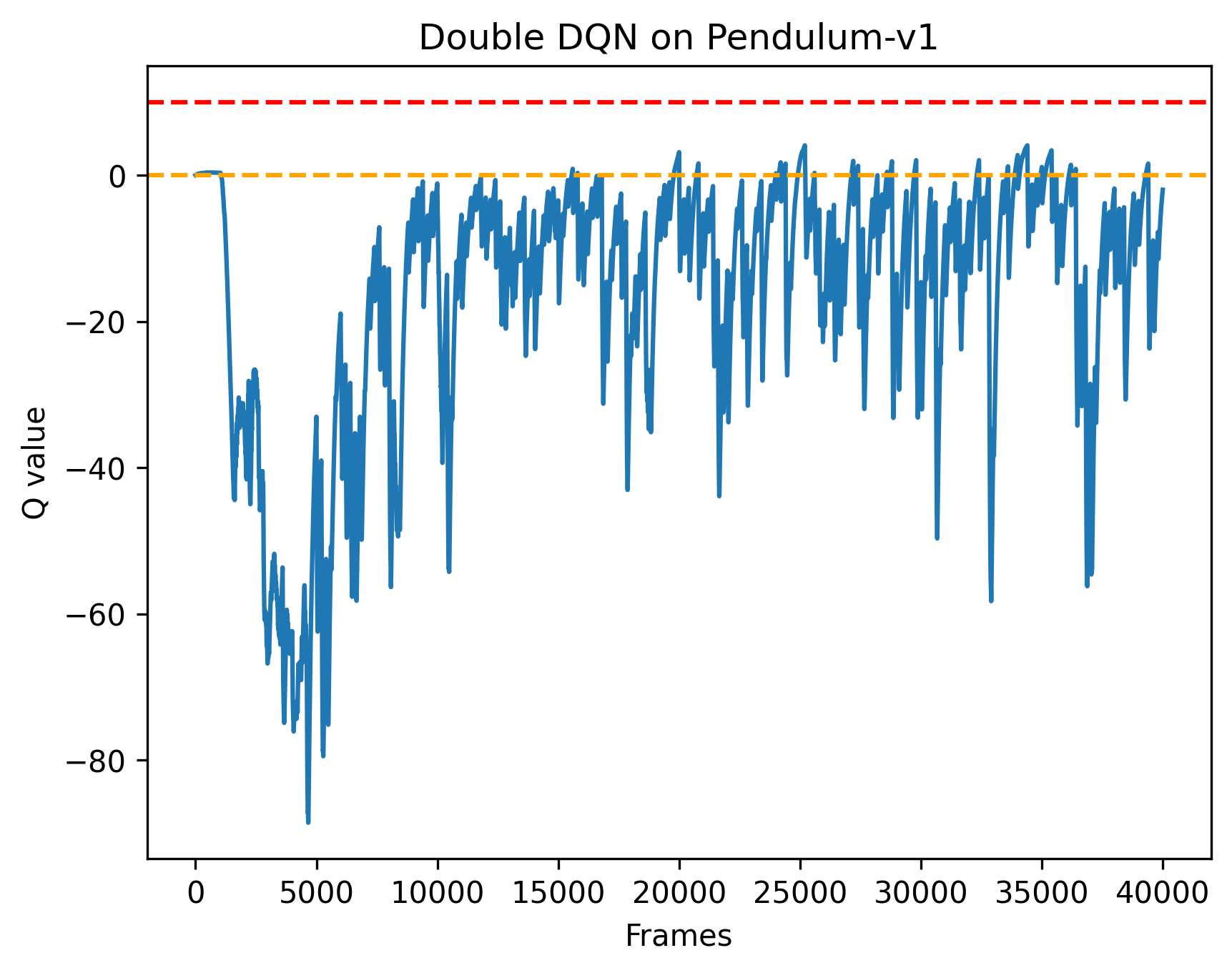
根据代码运行结果我们可以发现，DQN 算法在倒立摆环境中能取得不错的回报，最后的期望回报在-200 左右，但是不少值超过了 0，有一些还超过了 10，该现象便是 DQN 算法中的Q值过高估计。而Double DQN 比较少出现Q值大于 0 的情况，说明Q值过高估计的问题得到了很大缓解。

（七）Double DQN 的优势与适用场景

优势

1. 缓解过估计：核心价值，让 Q 值估计更接近真实值；
2. 收敛更稳定：过估计减少后，策略更新的信号更可靠，训练过程不易震荡；
3. 兼容性强：可以和 Dueling DQN、PER（优先经验回放）等其他 DQN 改进算法结合使用。

适用场景

• 所有原始 DQN 适用的场景（如 Atari 游戏、简单连续动作离散化的环境，如你代码中的 Pendulum）；
• 对 Q 值估计精度要求高的场景（比如稀疏奖励环境，过估计会导致智能体学不到有效策略）。

（八）关键总结

1. 核心改进：Double DQN 将 "选最优动作" 和 "评该动作的 Q 值" 拆分为两个网络（当前网络选动作，目标网络评价值），解决原始 DQN 的 Q 值过估计问题；
2. 公式核心 ：
   • 原始 DQN：；
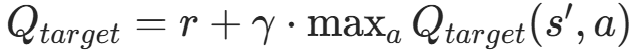   • Double 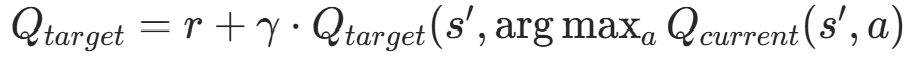DQN：；

Double DQN 是对原始 DQN 的轻量化改进，几乎不增加计算量，却能显著提升训练稳定性，是 DQN 系列算法中最经典的改进方向之一。

三、Dueling DQN 算法

（一）Dueling DQN 的提出背景：优化 Q 值的学习结构

原始 DQN（包括 Double DQN）的 Q 网络直接输出每个动作的 Q 值（Q(s,a)），但这种设计存在一个问题：

Q 值包含两个核心信息 ------「状态本身的价值」（比如 "倒立摆处于竖直位置" 这个状态本身就有高价值）和「动作相对于该状态的优势」（比如 "向左推" 比 "向右推" 在当前状态下更好），原始 DQN 将这两个信息混在一起学习，会导致冗余和低效。

举个例子：在 Pendulum（倒立摆）环境中，"摆杆接近竖直" 这个状态的价值远高于 "摆杆水平"，而动作的差异（比如选离散动作 3 还是 4）只是在 "优化这个高价值状态"，原始 DQN 无法区分这两种信息，学习效率会打折扣。

Dueling DQN 的核心目标就是将 Q 值拆分为 "状态价值" 和 "动作优势"，让网络分别学习这两种信息，提升学习效率和泛化能力。

（二）Dueling DQN 的核心思想：拆分 Q 值为 V (s) 和 A (s,a)

1. 核心公式：Q 值的拆解与重构

Dueling DQN 的核心是将 Q 值（状态 - 动作价值）拆分为两部分：Q(s,a)=V(s)+A(s,a)

• V(s)：状态价值函数 → 只和状态s有关，输出一个标量，表示 "处于状态s本身有多好"（和动作无关）；
• A(s,a)：动作优势函数 → 和状态s、动作a都有关，输出每个动作的优势值，表示 "在状态s下选动作a比选其他动作好多少"。

2. 关键改进：解决 "不可识别性" 问题

直接用 Q=V+A 会存在「不可识别性」：比如给V(s)加一个常数，同时给A(s,a)减同一个常数，Q(s,a)的值不变，但V和A的含义被破坏。

因此 Dueling DQN 引入中心化处理 ，重构 Q 值：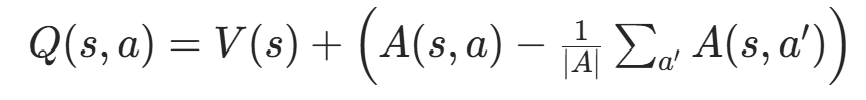

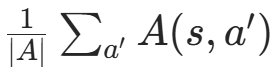• ：当前状态下所有动作优势值的均值；
• 作用：让优势函数A(s,a)表示 "相对于平均水平的优势"，既保留了动作间的相对差异，又解决了 V 和 A 的不可识别问题。

（三）Dueling DQN 的网络结构

VAnet类是 Dueling DQN 的核心实现，Qnet是原始 DQN 的网络，我将对比讲解：

1. 原始 DQN 的 Qnet（单层隐藏层）

class Qnet(torch.nn.Module):
    ''' 只有一层隐藏层的Q网络 '''
    def __init__(self, state_dim, hidden_dim, action_dim):
        super(Qnet, self).__init__()
        self.fc1 = torch.nn.Linear(state_dim, hidden_dim)  # 特征提取
        self.fc2 = torch.nn.Linear(hidden_dim, action_dim) # 直接输出每个动作的Q值

    def forward(self, x):
        x = F.relu(self.fc1(x))
        return self.fc2(x)  # 输出：[batch_size, action_dim] → 每个动作的Q值

• 逻辑：输入状态→提取特征→直接输出所有动作的 Q 值（混在一起学习 V 和 A）。

2. Dueling DQN 的 VAnet（拆分 V 和 A）

class VAnet(torch.nn.Module):
    ''' 只有一层隐藏层的A网络和V网络 '''
    def __init__(self, state_dim, hidden_dim, action_dim):
        super(VAnet, self).__init__()
        self.fc1 = torch.nn.Linear(state_dim, hidden_dim)  # 共享特征提取层
        self.fc_A = torch.nn.Linear(hidden_dim, action_dim) # 动作优势分支
        self.fc_V = torch.nn.Linear(hidden_dim, 1)          # 状态价值分支

    def forward(self, x):
        A = self.fc_A(F.relu(self.fc1(x)))  # 输出：[batch_size, action_dim] → 每个动作的优势值
        V = self.fc_V(F.relu(self.fc1(x)))  # 输出：[batch_size, 1] → 状态价值
        Q = V + A - A.mean(1).view(-1, 1)   # 重构Q值（中心化处理）
        return Q

代码逐行解析：

• self.fc1：所有分支共享的特征提取层（避免重复学习状态特征）；
• self.fc_A：输出每个动作的优势值A(s,a)，形状是[batch_size, action_dim]；
• self.fc_V：输出状态价值V(s)，形状是[batch_size, 1]；
• A.mean(1).view(-1, 1)：计算每个样本的优势值均值（mean(1)按行求均值，view保证维度匹配）；
• Q = V + A - A.mean(1).view(-1, 1)：对应公式Q=V+(A−Aˉ)，重构 Q 值。

（四）Dueling DQN 的训练逻辑（和原始 DQN 的异同）

DQN类的初始化和更新逻辑是兼容 Dueling DQN 的，核心异同点：

1. 初始化时的网络选择

if dqn_type == 'DuelingDQN':  # Dueling DQN采取不一样的网络框架
    self.q_net = VAnet(state_dim, hidden_dim, self.action_dim).to(device)
    self.target_q_net = VAnet(state_dim, hidden_dim, self.action_dim).to(device)
else:
    self.q_net = Qnet(state_dim, hidden_dim, self.action_dim).to(device)
    self.target_q_net = Qnet(state_dim, hidden_dim, self.action_dim).to(device)

• 逻辑：仅网络结构不同，Dueling DQN 用VAnet，原始 DQN 用Qnet；
• 注意：无论是VAnet还是Qnet，最终输出的都是[batch_size, action_dim]的 Q 值，因此后续的take_action、update逻辑完全复用（这是 Dueling DQN 的优势 ------ 对原有 DQN 框架侵入性极低）。

2. 训练 / 更新逻辑

Dueling DQN 的update函数和原始 DQN、Double DQN 完全一致：

• 计算当前 Q 值：q_values = self.q_net(states).gather(1, actions)；
• 计算目标 Q 值：q_targets = rewards + self.gamma * max_next_q_values * (1 - dones)；
• 损失计算：MSE 损失（）；
• 梯度下降更新网络。

核心差异 ：只是self.q_net的内部结构不同（拆分 V/A），但对外输出的 Q 值格式一致，因此训练流程无需修改。

（五）Dueling DQN 的Python代码完整实现

import random
import gymnasium as gym  
import numpy as np
import collections
from tqdm import tqdm
import torch
import torch.nn.functional as F
import matplotlib.pyplot as plt

class ReplayBuffer:
    ''' 经验回放池 '''
    def __init__(self, capacity):
        self.buffer = collections.deque(maxlen=capacity)  # 队列,先进先出

    def add(self, state, action, reward, next_state, done):  # 将数据加入buffer
        self.buffer.append((state, action, reward, next_state, done))

    def sample(self, batch_size):  # 从buffer中采样数据,数量为batch_size
        transitions = random.sample(self.buffer, batch_size)
        state, action, reward, next_state, done = zip(*transitions)
        return np.array(state), action, reward, np.array(next_state), done

    def size(self):  # 目前buffer中数据的数量
        return len(self.buffer)

def moving_average(a, window_size):
    ''' 滑动平均函数 '''
    cumulative_sum = np.cumsum(np.insert(a, 0, 0))
    middle = (cumulative_sum[window_size:] - cumulative_sum[:-window_size]) / window_size
    r = np.arange(1, window_size-1, 2)
    begin = np.cumsum(a[:window_size-1])[::2] / r
    end = (np.cumsum(a[:-window_size:-1])[::2] / r)[::-1]
    return np.concatenate((begin, middle, end))

class Qnet(torch.nn.Module):
    ''' 只有一层隐藏层的Q网络 '''
    def __init__(self, state_dim, hidden_dim, action_dim):
        super(Qnet, self).__init__()
        self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
        self.fc2 = torch.nn.Linear(hidden_dim, action_dim)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        return self.fc2(x)

class VAnet(torch.nn.Module):
    ''' 只有一层隐藏层的A网络和V网络 '''
    def __init__(self, state_dim, hidden_dim, action_dim):
        super(VAnet, self).__init__()
        self.fc1 = torch.nn.Linear(state_dim, hidden_dim)  # 共享网络部分
        self.fc_A = torch.nn.Linear(hidden_dim, action_dim)
        self.fc_V = torch.nn.Linear(hidden_dim, 1)

    def forward(self, x):
        A = self.fc_A(F.relu(self.fc1(x)))
        V = self.fc_V(F.relu(self.fc1(x)))
        Q = V + A - A.mean(1).view(-1, 1)  # Q值由V值和A值计算得到
        return Q

class DQN:
    ''' DQN算法,包括Double DQN和Dueling DQN '''
    def __init__(self,
                 state_dim,
                 hidden_dim,
                 action_dim,
                 learning_rate,
                 gamma,
                 epsilon,
                 target_update,
                 device,
                 dqn_type='VanillaDQN'):
        self.action_dim = action_dim
        if dqn_type == 'DuelingDQN':  # Dueling DQN采取不一样的网络框架
            self.q_net = VAnet(state_dim, hidden_dim,
                               self.action_dim).to(device)
            self.target_q_net = VAnet(state_dim, hidden_dim,
                                      self.action_dim).to(device)
        else:
            self.q_net = Qnet(state_dim, hidden_dim,
                              self.action_dim).to(device)
            self.target_q_net = Qnet(state_dim, hidden_dim,
                                     self.action_dim).to(device)
        self.optimizer = torch.optim.Adam(self.q_net.parameters(),
                                          lr=learning_rate)
        self.gamma = gamma
        self.epsilon = epsilon
        self.target_update = target_update
        self.count = 0
        self.dqn_type = dqn_type
        self.device = device

    def take_action(self, state):
        if np.random.random() < self.epsilon:
            action = np.random.randint(self.action_dim)
        else:
            # 优化张量创建：先转numpy数组再创建张量，消除效率警告
            state = torch.tensor(np.array([state]), dtype=torch.float32).to(self.device)
            action = self.q_net(state).argmax().item()
        return action

    def max_q_value(self, state):
        # 优化张量创建
        state = torch.tensor(np.array([state]), dtype=torch.float32).to(self.device)
        return self.q_net(state).max().item()

    def update(self, transition_dict):
        states = torch.tensor(transition_dict['states'],
                              dtype=torch.float32).to(self.device)
        actions = torch.tensor(transition_dict['actions']).view(-1, 1).to(
            self.device)
        rewards = torch.tensor(transition_dict['rewards'],
                               dtype=torch.float32).view(-1, 1).to(self.device)
        next_states = torch.tensor(transition_dict['next_states'],
                                   dtype=torch.float32).to(self.device)
        dones = torch.tensor(transition_dict['dones'],
                             dtype=torch.float32).view(-1, 1).to(self.device)

        q_values = self.q_net(states).gather(1, actions)
        if self.dqn_type == 'DoubleDQN':
            max_action = self.q_net(next_states).max(1)[1].view(-1, 1)
            max_next_q_values = self.target_q_net(next_states).gather(
                1, max_action)
        else:
            max_next_q_values = self.target_q_net(next_states).max(1)[0].view(
                -1, 1)
        q_targets = rewards + self.gamma * max_next_q_values * (1 - dones)
        dqn_loss = torch.mean(F.mse_loss(q_values, q_targets))
        self.optimizer.zero_grad()
        dqn_loss.backward()
        self.optimizer.step()

        if self.count % self.target_update == 0:
            self.target_q_net.load_state_dict(self.q_net.state_dict())
        self.count += 1

# 超参数设置
lr = 1e-2
num_episodes = 200
hidden_dim = 128
gamma = 0.98
epsilon = 0.01
target_update = 50
buffer_size = 5000
minimal_size = 1000
batch_size = 64
device = torch.device("cuda") if torch.cuda.is_available() else torch.device("cpu")

env_name = 'Pendulum-v1'
env = gym.make(env_name)
state_dim = env.observation_space.shape[0]
action_dim = 11  # 将连续动作分成11个离散动作

def dis_to_con(discrete_action, env, action_dim):  # 离散动作转回连续的函数
    action_lowbound = env.action_space.low[0]  # 连续动作的最小值
    action_upbound = env.action_space.high[0]  # 连续动作的最大值
    return action_lowbound + (discrete_action / (action_dim - 1)) * (action_upbound - action_lowbound)

def train_DQN(agent, env, num_episodes, replay_buffer, minimal_size, batch_size):
    return_list = []
    max_q_value_list = []
    max_q_value = 0
    for i in range(10):
        with tqdm(total=int(num_episodes / 10), desc='Iteration %d' % i) as pbar:
            for i_episode in range(int(num_episodes / 10)):
                episode_return = 0
                state, _ = env.reset()  # Gymnasium的reset返回(state, info)
                done = False
                while not done:
                    action = agent.take_action(state)
                    max_q_value = agent.max_q_value(state) * 0.005 + max_q_value * 0.995  # 平滑处理
                    max_q_value_list.append(max_q_value)  # 保存每个状态的最大Q值
                    action_continuous = dis_to_con(action, env, agent.action_dim)
                    # Gymnasium的step返回(next_state, reward, terminated, truncated, info)
                    next_state, reward, terminated, truncated, _ = env.step([action_continuous])
                    done = terminated or truncated  # 合并终止条件
                    replay_buffer.add(state, action, reward, next_state, done)
                    state = next_state
                    episode_return += reward
                    if replay_buffer.size() > minimal_size:
                        b_s, b_a, b_r, b_ns, b_d = replay_buffer.sample(batch_size)
                        transition_dict = {
                            'states': b_s,
                            'actions': b_a,
                            'next_states': b_ns,
                            'rewards': b_r,
                            'dones': b_d
                        }
                        agent.update(transition_dict)
                return_list.append(episode_return)
                if (i_episode + 1) % 10 == 0:
                    pbar.set_postfix({
                        'episode': '%d' % (num_episodes / 10 * i + i_episode + 1),
                        'return': '%.3f' % np.mean(return_list[-10:])
                    })
                pbar.update(1)
    return return_list, max_q_value_list

# 初始化并训练Dueling DQN
random.seed(0)
np.random.seed(0)
torch.manual_seed(0)
replay_buffer = ReplayBuffer(buffer_size)  # 使用本地定义的ReplayBuffer，避免rl_utils依赖
agent = DQN(state_dim, hidden_dim, action_dim, lr, gamma, epsilon,
            target_update, device, 'DuelingDQN')
return_list, max_q_value_list = train_DQN(agent, env, num_episodes,
                                          replay_buffer, minimal_size,
                                          batch_size)

# 绘制回报曲线
episodes_list = list(range(len(return_list)))
mv_return = moving_average(return_list, 5)  # 使用本地定义的滑动平均函数
plt.plot(episodes_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('Dueling DQN on {}'.format(env_name))
plt.savefig('DuelingDQN_Pendulum_returns.png', dpi=300, bbox_inches='tight')  # 保存回报图
plt.show()

# 绘制Q值变化曲线
frames_list = list(range(len(max_q_value_list)))
plt.plot(frames_list, max_q_value_list)
plt.axhline(0, c='orange', ls='--')
plt.axhline(10, c='red', ls='--')
plt.xlabel('Frames')
plt.ylabel('Q value')
plt.title('Dueling DQN on {}'.format(env_name))
plt.savefig('DuelingDQN_Pendulum_q_value.png', dpi=300, bbox_inches='tight')  # 保存Q值图
plt.show()

（六）程序运行结果展示与分析

结果展示

Iteration 0: 100%|██████████| 20/20 [00:05<00:00, 3.87it/s, episode=20, return=-1054.166]

Iteration 1: 100%|██████████| 20/20 [00:06<00:00, 2.97it/s, episode=40, return=-902.364]

Iteration 2: 100%|██████████| 20/20 [00:06<00:00, 2.87it/s, episode=60, return=-536.993]

Iteration 3: 100%|██████████| 20/20 [00:07<00:00, 2.84it/s, episode=80, return=-181.130]

Iteration 4: 100%|██████████| 20/20 [00:07<00:00, 2.73it/s, episode=100, return=-356.823]

Iteration 5: 100%|██████████| 20/20 [00:07<00:00, 2.66it/s, episode=120, return=-235.687]

Iteration 6: 100%|██████████| 20/20 [00:08<00:00, 2.29it/s, episode=140, return=-176.851]

Iteration 7: 100%|██████████| 20/20 [00:09<00:00, 2.09it/s, episode=160, return=-149.947]

Iteration 8: 100%|██████████| 20/20 [00:09<00:00, 2.06it/s, episode=180, return=-237.035]

Iteration 9: 100%|██████████| 20/20 [00:09<00:00, 2.00it/s, episode=200, return=-136.091]

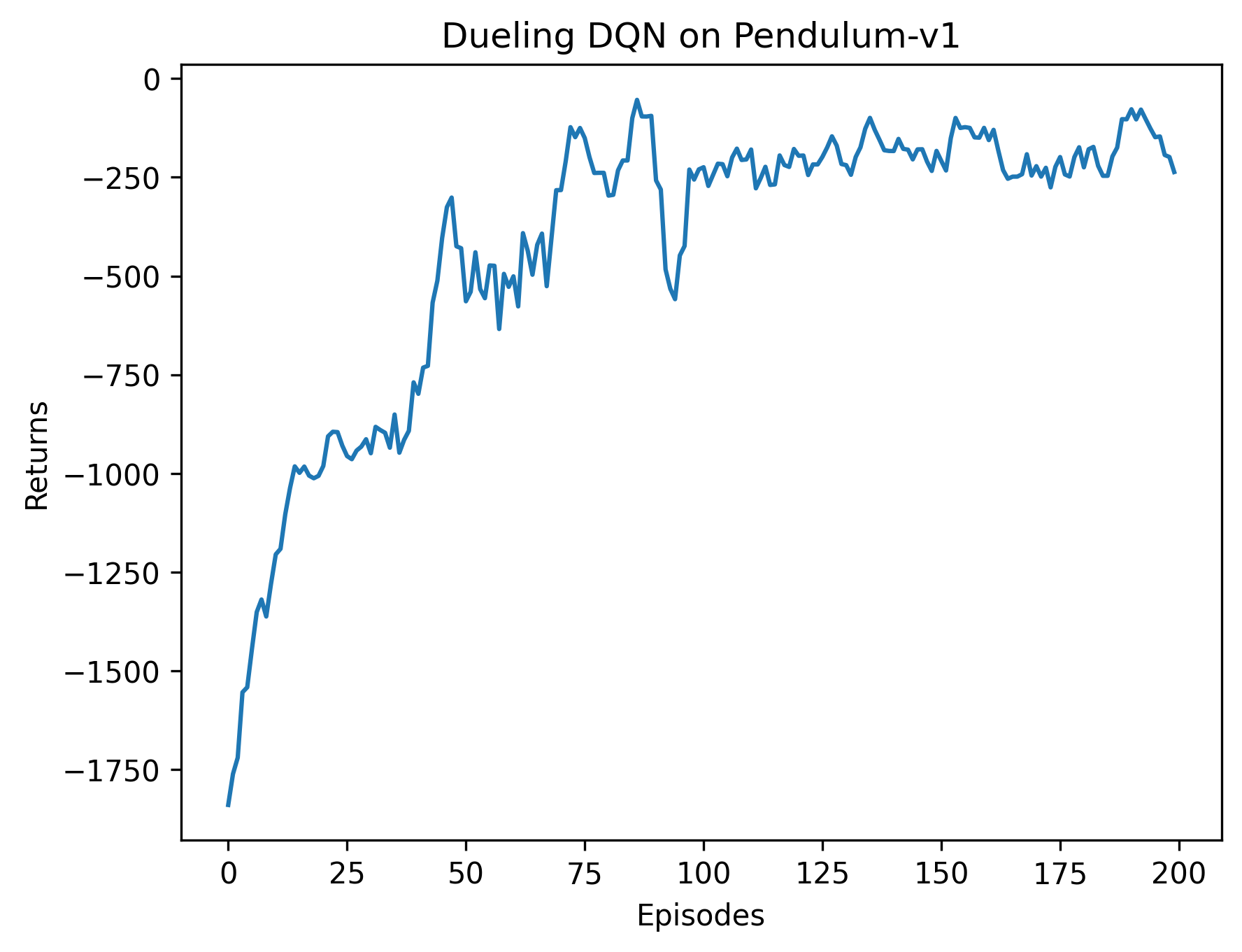
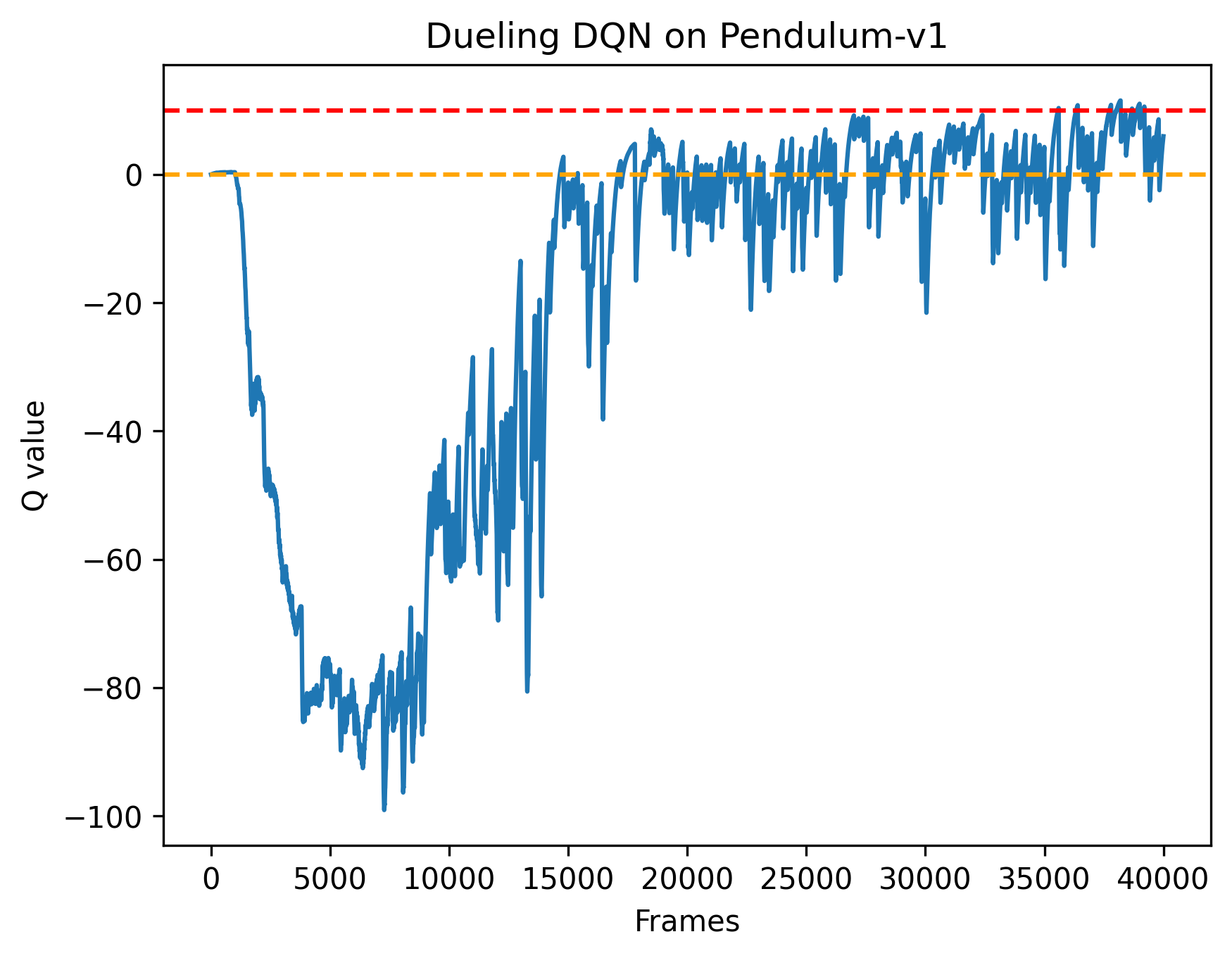
结果分析

根据代码运行结果我们可以发现，相比于传统的 DQN，Dueling DQN 在多个动作选择下的学习更加稳定，得到的回报最大值也更大。由 Dueling DQN 的原理可知，随着动作空间的增大，Dueling DQN 相比于 DQN 的优势更为明显。之前我们在环境中设置的离散动作数为 11，我们可以增加离散动作数（例如 15、25 等），继续进行对比实验。

（七）Dueling DQN 的优势与适用场景

核心优势

1. 学习效率更高：拆分 V 和 A 后，网络可以分别学习 "状态本身的价值" 和 "动作的相对优势"，避免信息混叠导致的冗余学习；
2. 泛化能力更强：对于 "状态价值主导" 的场景（比如 Pendulum、Atari 游戏中的 "安全区域"），V (s) 可以快速学到状态的核心价值，A (s,a) 只需微调动作选择；
3. 框架兼容好：可以和 Double DQN、PER（优先经验回放）等其他 DQN 改进算法结合（比如 Dueling+Double DQN），进一步提升性能；
4. 计算开销低：仅增加了一个线性层（fc_V），几乎不增加训练时间。

适用场景

• 状态价值主导的环境：比如 Pendulum（摆杆位置决定核心价值）、迷宫类环境（是否靠近终点决定核心价值）；
• 动作空间较大的环境：拆分后 A (s,a) 只需学习动作间的相对差异，而非绝对 Q 值，降低学习难度；
• 希望提升收敛速度的场景：Dueling DQN 通常比原始 DQN 收敛更快，且最终回报更高。

（八）Dueling DQN vs Double DQN：核心区别

很多人会混淆这两种算法，这里做清晰对比：

维度	Double DQN	Dueling DQN
核心目标	缓解 Q 值过估计（拆分 "选动作" 和 "评价值"）	提升学习效率（拆分 "状态价值" 和 "动作优势"）
改进层面	目标 Q 值的计算逻辑	Q 网络的内部结构
对代码的修改点	update函数中目标 Q 值的计算	Q 网络的定义（VAnet 替代 Qnet）
兼容性	可与 Dueling DQN 结合（Dueling+Double）	可与 Double DQN、PER 等结合

（九）关键总结

1. 核心思想：Dueling DQN 将 Q 值拆分为状态价值V(s)（和动作无关）和动作优势A(s,a)（和动作有关），并通过中心化处理（A−Aˉ）解决不可识别性问题；
2. 代码核心 ：VAnet类是关键 ------ 共享特征提取层 + V 分支 + A 分支，最终重构 Q 值；
3. 训练逻辑：对外输出的 Q 值格式和原始 DQN 一致，因此训练 / 更新流程无需修改；
4. 核心优势：学习效率更高、收敛更快，且可与 Double DQN 等算法结合，是 DQN 算法的重要改进方向。

Dueling DQN 的核心就是VAnet类的实现 ------ 通过拆分 V 和 A 重构 Q 值，让网络更高效地学习状态和动作的价值信息。

四、总结

在传统的 DQN 基础上，有两种非常容易实现的变式------Double DQN 和 Dueling DQN，Double DQN 解决了 DQN 中对Q值的过高估计，而 Dueling DQN 能够很好地学习到不同动作的差异性，在动作空间较大的环境下非常有效。从 Double DQN 和 Dueling DQN 的方法原理中，我们也能感受到深度强化学习的研究是在关注深度学习和强化学习有效结合：一是在深度学习的模块的基础上，强化学习方法如何更加有效地工作，并避免深度模型学习行为带来的一些问题，例如使用 Double DQN 解决Q值过高估计的问题；二是在强化学习的场景下，深度学习模型如何有效学习到有用的模式，例如设计 Dueling DQN 网络架构来高效地学习状态价值函数以及动作优势函数。