《智能的理论》全书转至目录****
不同AGI的研究路线对比简化版:《AGI(具身智能)路线对比》,欢迎各位参与讨论、批评或建议。
一.视角(Goldstein和Brockmole(著),张明(译),2018)
视角指物体在人眼视网膜的角度。眼球有360°,因此1°视角的物体只占其1/360,在成人眼睛里1°视角约为0.3毫米。视角与刺激的大小有关,刺激越大,视角越大,反之则越小。如图1所示,视角还取决于刺激与观察者间的距离,对于相同大小的刺激,当刺激越近时,视角变大,反之则越小。
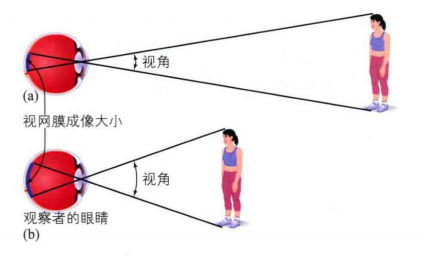
图1
"拇指技术"是粗略测量视角的一个方法。伸直手臂注视拇指,处于手臂长度位置的手指宽度约为2°视角。因此被拇指刚刚好能遮挡的客体的视角约为2°。如图2所示,当母子刚刚好能把手机遮住时,手机的视角也为2°。这也说明了视角与距离有关,调整客体的距离过后,近处的小物体(如手指)的和远处的大物体(如手机)可以具有相同的视角。
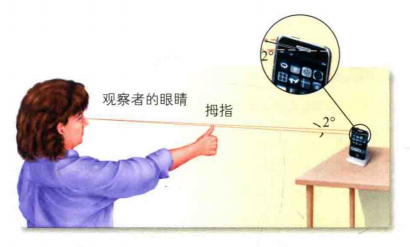
图2
二.大小恒常性(Goldstein和Brockmole(著),张明(译),2018)
远处物体的视角很小,相反近处物体的视角较大,但是现实生活中视角的大小很难影响我们对物体真实大小的判断。比如当你在道路上开车,道路两旁都有植树,离你近的树所占的视角大,离你远的树的视角小,但是你并不会觉得远处的树会比近处的小。这个现象被称为大小恒常性。
对于这种现象,Gregory(1966)提出了一种解释机制:S=k(R*D),k是常数,R是视网膜的视角大小,D表示物体与眼睛的距离,S是对刺激的大小知觉。由于距离和视网膜大小会互相补偿,使人对物体的知觉保持一致(远处的树视角虽然小,但是远距离可以补偿大小知觉)。
三.距离与大小知觉(Goldstein和Brockmole(著),张明(译),2018)
在Holway和Boring(1941)的实验中,被试坐在两走廊的交叉口,需要观察右侧走廊里的一个发光的测试圆,同时也需要观察左侧走廊里的一个发光的对比圆。对比圆与被试的距离始终是3米,而测试圆的距离在3~36米变化。固定位置的对比圆的大小可以调节,被试的任务是调节对比圆的直径,以匹配对测试圆的大小的知觉(而非测试圆的视角),如图3。
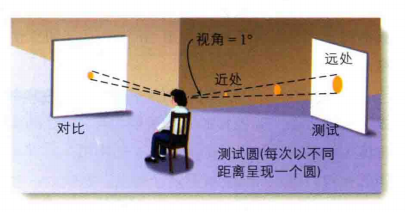
图3
在实验中,存在许多可用的深度线索,包括双眼像差、运动透视和阴影等。因此研究者设置了不同的实验条件以消除这些深度线索(比如用单眼观察,以消除双眼像差;在走廊加上帘子,以消除阴影等)。研究结果发现,当被试能利用全部深度知觉时,被试所判断的测试圆的大小与真实大小相匹配。相反,当消除的深度线索越多时,被试对测试圆大小的判断就变得更不准确。这说明,距离对大小知觉判断有重要影响。有趣的是,当所有深度线索都被消除后,被试的大小知觉便不是由测试圆的真实大小确定,而是由圆在观察者视网膜上的视角决定的(这时,大小知觉判断可以粗略解释为:S=R)。
由于宇宙的巧合,太阳和月球具有相同的视角。并且由于不能判断它们的距离,因此我们只能根据视角判断它们的大小。对太阳和月球大小的知觉只能依赖于其视角的一个例子是,当日食发生时,尽管能看到月球周围太阳的光晕,但月球几乎遮挡了整个太阳。
四.影响知觉判断的其他因素(Goldstein和Brockmole(著),张明(译),2018)
环境中的其他信息也有助于保持大小恒常性。比如对物体的熟悉度就是其中之一。例如,一个成人无论他在视网膜上的视角大小如何,其身高范围大致是确定的。
相对大小的对比。我们总是对篮球运动员的身高判断错误,尤其是当对比的对象都是篮球运动员时。只有当一个标准身高的人站在他们中间时,才能估计运动员的真实身高。
地面上的纹理信息。如图4,由于它们底部所占的铺路石的数量相同,所以可以判断它们的大小相同。

图4