我爱学算法之—— 递归

一、汉诺塔问题

题目解析

经典汉诺塔问题：三根柱子（A、B、C），N个不同大小的圆盘。

初始状态：N个大小不同的圆盘按照大小（一个盘子上只能放比自己小的盘子）依次套在第一个柱子（A）上。

我们可以按照以下规则移动圆盘：

每次只能移动一个圆盘
每次只能移动柱子顶端的圆盘
圆盘只能放在比自己的圆盘上

结束状态：A柱子上的所有盘子，移动到C柱子上。

算法思路

这里N个圆盘（N可以是1,2,3,4,5...)

当 N 等于 1 时：将圆盘从A柱子移动到C柱子即可；

当 N 等于 2 时：将A柱上的 1 个圆盘先移动到B柱上，再将A柱上第2个圆盘移动到C柱上，最后将B柱上的圆盘移动到C柱上即可；

当 N 等于 3 时：将A柱上的 2 个圆盘移动到B柱上，再将A柱上第3个圆盘移动到C柱上，最后将B柱上的圆盘移动到C柱上即可；（N=2时，移动圆盘）

依次类推，可以发现，当 N > 2 时，将圆盘从A柱移动到C柱上，就只有三个步骤：

现将A柱上的N-1个圆盘移动到B柱上
再将A柱上的最后一个圆盘移动到C柱上
最后将B柱上的N-1个圆盘移动到C柱上

所以，移动圆盘的整体逻辑就可以看成：

将X柱上的 N 个圆盘，借助Y柱，移动到Z柱上 （当N == 1时，直接将X柱上的圆盘移动到C柱上即可）

代码实现

cpp 复制代码

class Solution {
public:
    void dfs(vector<int>& x, vector<int>& y, vector<int>& z, int n) {
        if (n == 1) {
            z.push_back(x.back());
            x.pop_back();
            return;
        }
        // 将x柱 n-1个圆盘借助z柱 移动到 y柱上
        dfs(x, z, y, n - 1);
        // 将x柱 最后一个光盘移动到z柱
        z.push_back(x.back());
        x.pop_back();
        // 将y柱 n-1个圆盘借助x柱 移动到z柱上
        dfs(y, x, z, n - 1);
    }
    void hanota(vector<int>& A, vector<int>& B, vector<int>& C) {
        dfs(A, B, C, A.size());
    }
};

二、合并两个有序链表

题目解析

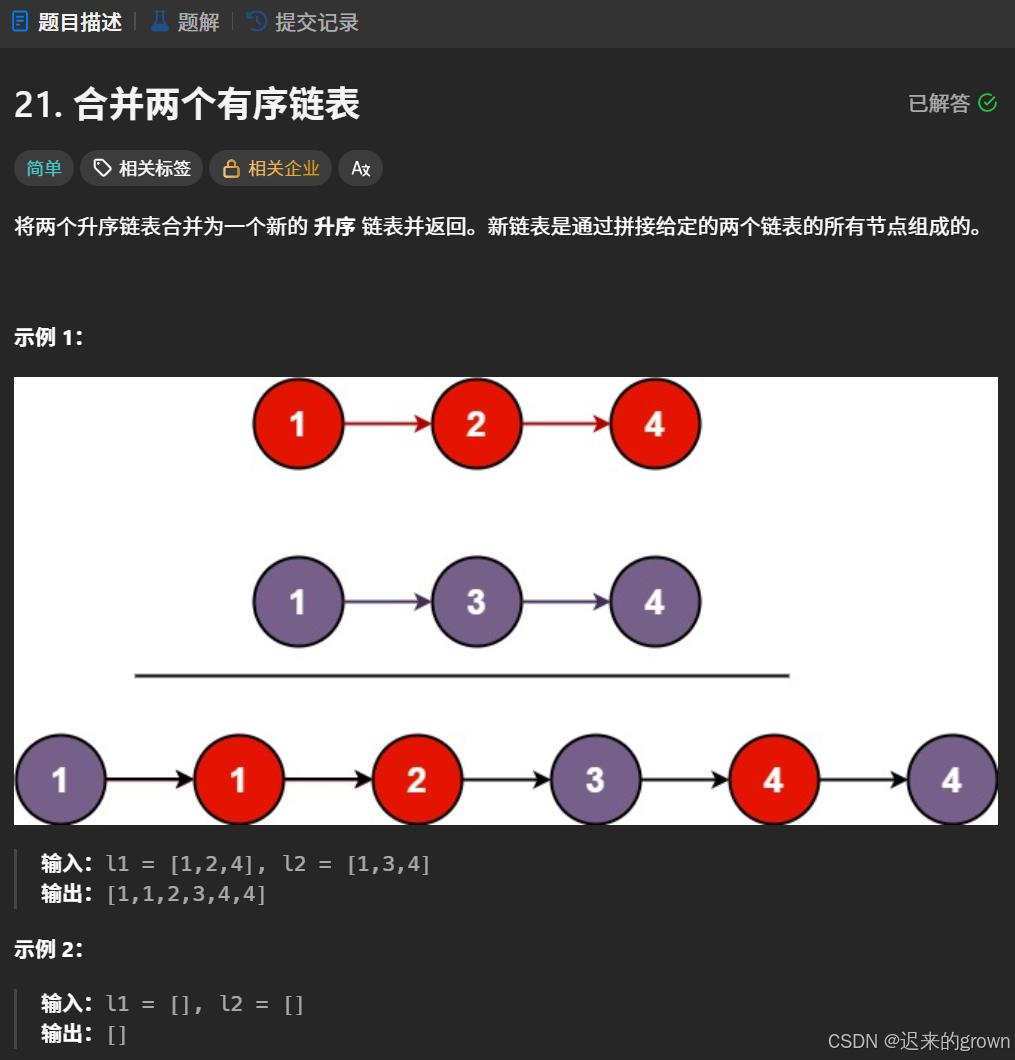
合并两个有序链表，这道题除了使用双指针，也可以使用递归来解决；

算法思路

合并链两个有序链表（升序），回想双指针遍历的过程，无非就是依次比较两个节点值的大小，然后修改指针指向。

cur1和cur2指针遍历两个链表，将值较小的节点放入新链表中

cur1->val < cur2->val：将cur1节点放入新链表中，然后cur1指针向后遍历。（这个过程是不是可以看做：合并以cur1的下一个节点作为头结点和以cur2为头结点的两个链表，最后返回一个合并后新链表的头结点）
cur1->val >= cur2->val：将cur2节点放入新链表中，然后cur2指针向后遍历。（这个过程是不是可以看做：合并以cur1作为头结点和以cur2的下一个节点作为头结点的两个链表，最后返回一个合并后新链表的头结点）

所以，使用递归来解决这道题那就非常简单了：

dfs函数就是完成合并cur1和cur2两个有序链表，最后返回合并后链表的头结点。

判断cur1和cur2是否为空
判断cur1->val 和 cur2->val 的大小关系，更新合并后链表的头结点
1. 如果cur1->val < cur1->val ：合并cur1-next、cur2两个有序链表，返回新链表的头结点
2. 否则，合并cur1、cur2->next两个有序链表，返回新链表的头结点
最后，返回合并后链表的头结点。

代码实现

cpp 复制代码

class Solution {
public:
    ListNode* dfs(ListNode* cur1, ListNode* cur2) {
        if (cur1 == nullptr)
            return cur2;
        if (cur2 == nullptr)
            return cur1;
        ListNode* ret = nullptr;
        if (cur1->val < cur2->val) {
            ret = cur1;
            ret->next = dfs(cur1->next, cur2);
        } else {
            ret = cur2;
            ret->next = dfs(cur1, cur2->next);
        }
        return ret;
    }
    ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
        return dfs(list1, list2);
    }
};

三、反转链表

题目解析

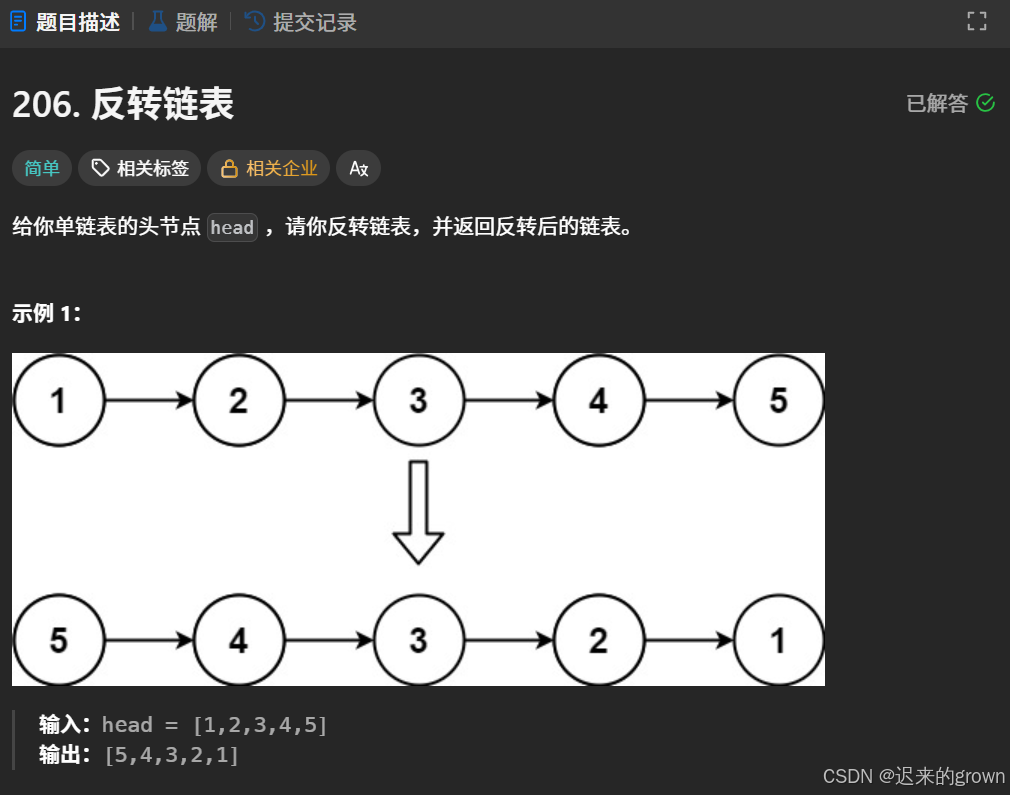
给定一个单链表的头结点，我们要反转该链表，然后返回反转后的链表

算法思路

这道题可以说是非常easy了，我们可以使用三指针依次修改链表指向。

这里我们想，能否使用递归来解决呢？

要使用递归来解决，那递归函数要完成的功能就是：反转单链表，然后返回反转后链表的头结点

当链表为空或者只有一个节点时（node == nullptr || node->next == nullptr）：直接返回node即可

当链表中节点个数大于等于2时：反转以node->next为根节点的头结点，然后将node节点放到新链表的结尾。

这里要将node放到新链表的结尾，而node->next就是反转后链表的最后一个节点。

这里直接获取反转后新链表的头结点，然后修改指针的指向即可

代码实现

cpp 复制代码

class Solution {
public:
    ListNode* dfs(ListNode* node) {
        if (node == nullptr || node->next == nullptr)
            return node;
        ListNode* rhead = dfs(node->next);
        node->next->next = node;
        node->next = nullptr;
        return rhead;
    }
    ListNode* reverseList(ListNode* head) { return dfs(head); }
};

四、两两交换链表中的节点

题目解析

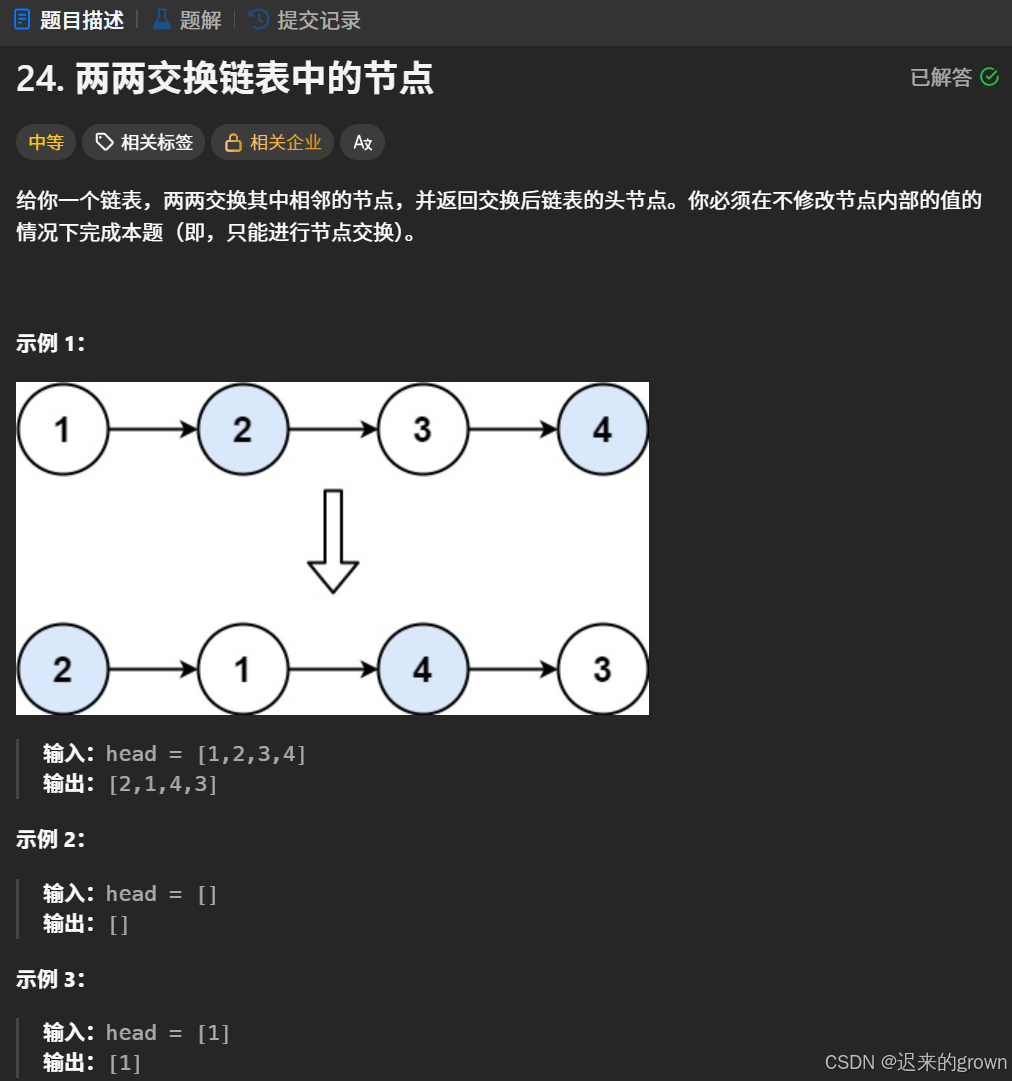
给定一个单链表，我们要两两交换其中相邻的节点，最后返回交换后链表的头结点

算法思路

之前在学习链表相关的算法时，使用指针遍历链表，使用头插法交换两个相邻链表节点，最后返回新链表的头结点。

这里我们使用递归的思路来解决这道问题

根据上述使用递归来解决问题的思路，这道题的大致思路：递归完成后续节点的两两交换，然后进行当前节点node和node->next节点的交换。

如果node == nullptr || node->next == nullptr ：直接返回即可
递归完成后续链表的相邻节点的两两交换，获取后续链表交换后的头结点
完成node和node->next节点的交换，记录交换后的头结点，然后返回。

代码实现

cpp 复制代码

class Solution {
public:
    ListNode* dfs(ListNode* node)
    {
        if(node == nullptr || node->next == nullptr)
            return node;
        // 两两交换后续链表，获取交换后的头结点
        ListNode* next = dfs(node->next->next);
        // 交换node和node->next节点
        ListNode* prev = node;
        ListNode* cur = node->next;
        cur->next = prev;
        prev->next = next;
        // 返回交换后的头结点
        return cur;
    }
    ListNode* swapPairs(ListNode* head) {
        return dfs(head);
    }
};

五、Pow(x, n)

题目解析

这道题要实现pow(x,n)，计算x的n次幂（n是正整数）

算法思路

要求x的n次幂，可以说是每次简单的

无非就是递归求x的n-1次幂，然后再乘上x返回即可；但是这样未免也太复杂了些。

这里我们可以每次计算x的n/2次幂，然后将结果相乘，就可以求出x的n次幂；

细节：

当n是奇数时时，那x的n/2次幂乘上x的n/2次幂就是x的n-1次幂，计算结果不正确；这里就需要进行特殊判断：

如果n%2 != 0 ：返回tmp*tmp*x

如果n%2 == 0 ：返回tmp*tmp

注意：这道题中n是可以<0的，而在递归逻辑中是当n == 0时返回1；这里就要进行特殊处理：当n<0时，就计算x / 1.0的abs(n)次幂。

代码实现

cpp 复制代码

class Solution {
public:
    double dfs(double x, int n) {
        if (n == 0)
            return 1;
        double tmp = dfs(x, n / 2);
        return n % 2 == 0 ? tmp * tmp : tmp * tmp * x;
    }
    double myPow(double x, int n) {
        long long cnt = n;
        if (n < 0) {
            x = 1.0 / x;
            cnt = -cnt;
        }
        return dfs(x, cnt);
    }
};

六、计算布尔二叉树的值

题目解析

一个完整二叉树，叶子节点值为0或1（False或True）、非叶子节点的值为2或3（逻辑或、逻辑与）

要遍历给定的完整二叉树，然后计算根节点的布尔运算值，最后返回。

算法思路

这道题整体思路还是非常简单的，采用后续遍历，获取左右子树的布尔运算值，然后计算，最后返回即可。

代码实现

cpp 复制代码

class Solution {
public:
    bool dfs(TreeNode* root)
    {
        if(root->val == 0)
            return false;
        if(root->val == 1)
            return true;
        if(root->val == 2)
            return dfs(root->left) || dfs(root->right);
        if(root->val == 3)
            return dfs(root->left) && dfs(root->right);
        return false;
    }
    bool evaluateTree(TreeNode* root) {
        if(root == nullptr)
            return false;
        return dfs(root);
    }
};

本篇文章到这里就结束了，感谢支持

我的博客即将同步至腾讯云开发者社区，邀请大家一同入驻：https://cloud.tencent.com/developer/support-plan?invite_code=2oul0hvapjsws