设被采样信号为:x(t) = cos(2*pi*f0*t + ϕ),采样率为fs
如果 f0大于采样频率fs,则混叠后的频率为f1 = |f0 -- k*fs|,也就是说即使f0大于fs,混叠之后频率范围也是在0~fs之间了。所以我们只考虑f0在0~fs之间的情况,0~fs/2对应正频率分量,fs/2~fs对应负频率分量,对于实数而言,负频率分量就是正频率分量的共轭,我们只关注正频率分量,并以正频率分量为基准:
如果f0 < fs/2 , 则采样的信号后 xa(t) =cos(2*pi*f0*nT + ϕ) = cos(2*pi*f0/fs*n + ϕ)
如果f0 > fs/2 , 则采样的信号后 xa(t) =cos(2*pi*f0*nT + ϕ) = cos(2*pi*(fs+(f0-fs))/fs*n + ϕ) = cos(-2*pi*(fs-f0)/fs*n + ϕ) = cos(2*pi*(fs-f0)/fs*n - ϕ)
也就是说,对应正频率的部分相位会变反,这就是欠采样时的相位倒置现象。
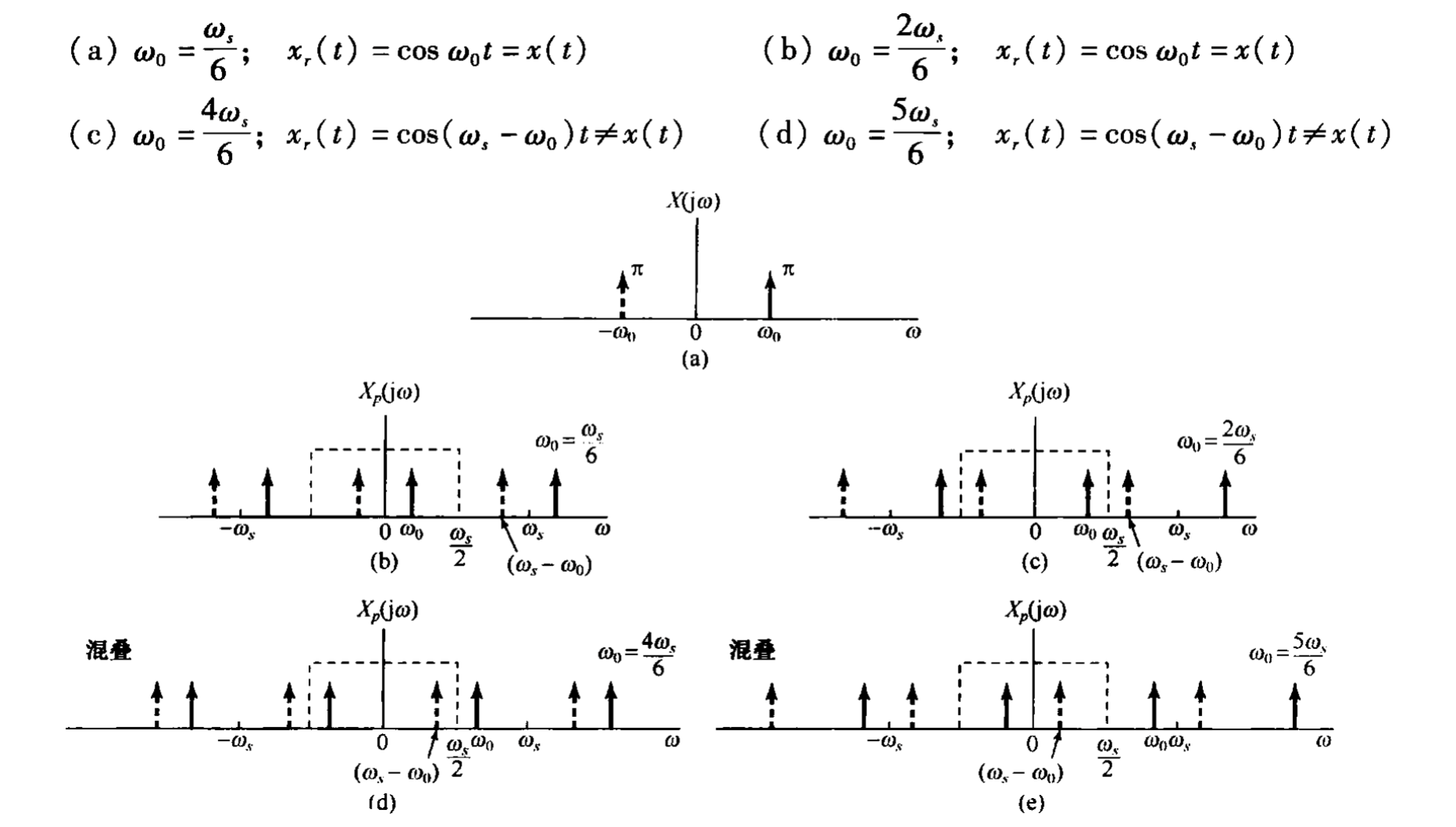
另外,奈奎斯特采样定理虽然要求采样频率大于信号频率的2倍,但有时候利用欠采样,也可以突破这个限制,只需要满足采样频率大于信号带宽的两倍,但需要满足两个条件:
(1)不需要考虑在第(2*k)奈奎斯特区间的相位倒置问题(k为正整数);
(2)被采样信号的频率只能处于单一的奈奎斯特区间内,不能跨过奈奎斯特区间。