目录
[1.1 C语言算法的独特魅力](#1.1 C语言算法的独特魅力)
[1.2 算法复杂度分析的C语言视角](#1.2 算法复杂度分析的C语言视角)
[2.1 查找算法:从线性到二分](#2.1 查找算法:从线性到二分)
[2.2 排序算法:手写经典实现](#2.2 排序算法:手写经典实现)
[3.1 数学函数实现](#3.1 数学函数实现)
[3.2 随机数生成算法](#3.2 随机数生成算法)
[4.1 字符串匹配算法](#4.1 字符串匹配算法)
[5.1 链表算法](#5.1 链表算法)
[5.2 树算法](#5.2 树算法)
[6.1 经典DP问题](#6.1 经典DP问题)
[6.2 路径规划算法](#6.2 路径规划算法)

如果您喜欢此文章,请收藏、点赞、评论,谢谢,祝您快乐每一天。
一、C语言算法设计的核心哲学
1.1 C语言算法的独特魅力
C语言算法的核心在于贴近硬件、控制精确、效率至上。与高级语言不同,C语言算法设计需要:
- 手动内存管理:每个字节都要心中有数
- 指针操作艺术:直接内存访问,威力与风险并存
- 零开销抽象:不依赖运行时,性能可预测
- 跨平台兼容:编写可移植的高效算法
1.2 算法复杂度分析的C语言视角
// 时间复杂度直观理解
O(1) → 直接数组访问 arr[i]
O(log n) → 二分查找
O(n) → 线性遍历链表
O(n log n)→ 快速排序
O(n²) → 冒泡排序
O(2ⁿ) → 汉诺塔递归
// 空间复杂度考量
// C语言需要显式管理栈和堆内存
void recursive_func(int n) {
int local_var; // 栈空间:O(1) per call
int* heap_mem = malloc(n * sizeof(int)); // 堆空间:O(n)
// 递归调用栈深度影响总空间复杂度
}
二、基础算法实战
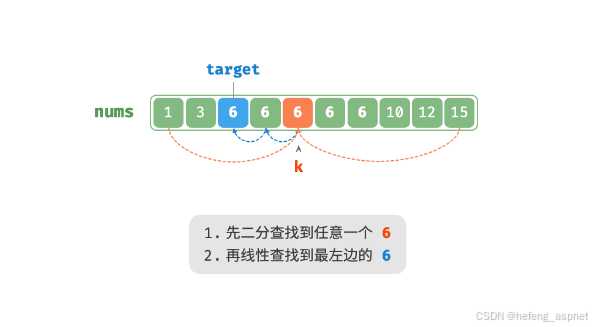
2.1 查找算法:从线性到二分
// 1. 线性查找:通用但低效
int linear_search(int arr[], int n, int target) {
for (int i = 0; i < n; i++) {
if (arr[i] == target) {
return i; // 返回索引
}
}
return -1; // 未找到
}
// 2. 二分查找:有序数组的利器
int binary_search(int arr[], int n, int target) {
int left = 0, right = n - 1;
while (left <= right) {
int mid = left + (right - left) / 2; // 防止溢出
if (arr[mid] == target) {
return mid;
} else if (arr[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return -1;
}
// 3. 插值查找:均匀分布数据的优化
int interpolation_search(int arr[], int n, int target) {
int low = 0, high = n - 1;
while (low <= high && target >= arr[low] && target <= arr[high]) {
if (low == high) {
return (arr[low] == target) ? low : -1;
}
// 关键:使用插值公式估算位置
int pos = low + ((double)(high - low) /
(arr[high] - arr[low])) * (target - arr[low]);
if (arr[pos] == target) {
return pos;
} else if (arr[pos] < target) {
low = pos + 1;
} else {
high = pos - 1;
}
}
return -1;
}
2.2 排序算法:手写经典实现
// 1. 冒泡排序:教学意义大于实用
void bubble_sort(int arr[], int n) {
for (int i = 0; i < n - 1; i++) {
int swapped = 0; // 优化:检查是否已排序
for (int j = 0; j < n - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
// 交换
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
swapped = 1;
}
}
if (!swapped) break; // 提前终止
}
}
// 2. 快速排序:分治思想的典范
void quick_sort(int arr[], int low, int high) {
if (low < high) {
// 分区操作
int pivot = partition(arr, low, high);
// 递归排序左右两部分
quick_sort(arr, low, pivot - 1);
quick_sort(arr, pivot + 1, high);
}
}
int partition(int arr[], int low, int high) {
int pivot = arr[high]; // 选择最后一个元素作为基准
int i = low - 1; // 较小元素的索引
for (int j = low; j < high; j++) {
if (arr[j] <= pivot) {
i++;
// 交换arr[i]和arr[j]
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
// 将基准放到正确位置
int temp = arr[i + 1];
arr[i + 1] = arr[high];
arr[high] = temp;
return i + 1;
}
// 3. 归并排序:稳定排序的代表
void merge_sort(int arr[], int left, int right) {
if (left < right) {
int mid = left + (right - left) / 2;
merge_sort(arr, left, mid);
merge_sort(arr, mid + 1, right);
merge(arr, left, mid, right);
}
}
void merge(int arr[], int left, int mid, int right) {
int n1 = mid - left + 1;
int n2 = right - mid;
// 创建临时数组
int* L = malloc(n1 * sizeof(int));
int* R = malloc(n2 * sizeof(int));
// 复制数据
for (int i = 0; i < n1; i++) L[i] = arr[left + i];
for (int j = 0; j < n2; j++) R[j] = arr[mid + 1 + j];
// 合并临时数组
int i = 0, j = 0, k = left;
while (i < n1 && j < n2) {
if (L[i] <= R[j]) {
arr[k] = L[i];
i++;
} else {
arr[k] = R[j];
j++;
}
k++;
}
// 复制剩余元素
while (i < n1) arr[k++] = L[i++];
while (j < n2) arr[k++] = R[j++];
free(L);
free(R);
}

三、数值计算算法
3.1 数学函数实现
// 1. 平方根算法:牛顿迭代法
double sqrt_newton(double x, double epsilon) {
if (x < 0) return -1.0; // 错误处理
double guess = x / 2.0;
double prev_guess;
do {
prev_guess = guess;
guess = (guess + x / guess) / 2.0;
} while (fabs(guess - prev_guess) > epsilon);
return guess;
}
// 2. 幂运算:快速幂算法
double power(double base, int exponent) {
if (exponent == 0) return 1.0;
if (exponent == 1) return base;
double result = 1.0;
double current = base;
int exp = abs(exponent);
while (exp > 0) {
if (exp & 1) { // 当前位为1
result *= current;
}
current *= current; // 平方
exp >>= 1; // 右移一位
}
return (exponent > 0) ? result : 1.0 / result;
}
// 3. 最大公约数:欧几里得算法
int gcd(int a, int b) {
while (b != 0) {
int temp = b;
b = a % b;
a = temp;
}
return a;
}
// 扩展欧几里得算法:求解ax + by = gcd(a,b)
struct ExtendedGCD {
int gcd;
int x;
int y;
};
struct ExtendedGCD extended_gcd(int a, int b) {
if (b == 0) {
return (struct ExtendedGCD){a, 1, 0};
}
struct ExtendedGCD result = extended_gcd(b, a % b);
return (struct ExtendedGCD){
result.gcd,
result.y,
result.x - (a / b) * result.y
};
}
3.2 随机数生成算法
// 线性同余生成器(LCG)
unsigned long lcg_seed = 1;
unsigned int lcg_rand() {
// 常用参数:a=1664525, c=1013904223, m=2^32
lcg_seed = (1664525UL * lcg_seed + 1013904223UL) & 0xFFFFFFFF;
return (unsigned int)(lcg_seed >> 16); // 返回高16位
}
// 梅森旋转算法(简化版)
#define MT_N 624
#define MT_M 397
static unsigned long mt[MT_N];
static int mt_index = MT_N + 1;
void mt_init(unsigned long seed) {
mt[0] = seed & 0xFFFFFFFFUL;
for (int i = 1; i < MT_N; i++) {
mt[i] = (1812433253UL * (mt[i-1] ^ (mt[i-1] >> 30)) + i) & 0xFFFFFFFFUL;
}
mt_index = MT_N;
}
unsigned long mt_rand() {
if (mt_index >= MT_N) {
// 生成新的一批随机数
static unsigned long mag01[2] = {0x0UL, 0x9908B0DFUL};
for (int i = 0; i < MT_N; i++) {
unsigned long y = (mt[i] & 0x80000000UL) | (mt[(i+1) % MT_N] & 0x7FFFFFFFUL);
mt[i] = mt[(i+MT_M) % MT_N] ^ (y >> 1) ^ mag01[y & 0x1UL];
}
mt_index = 0;
}
unsigned long y = mt[mt_index++];
// 温度变换
y ^= (y >> 11);
y ^= (y << 7) & 0x9D2C5680UL;
y ^= (y << 15) & 0xEFC60000UL;
y ^= (y >> 18);
return y;
}

四、字符串处理算法
4.1 字符串匹配算法
// 1. 朴素字符串匹配
int naive_search(const char* text, const char* pattern) {
int n = strlen(text);
int m = strlen(pattern);
for (int i = 0; i <= n - m; i++) {
int j;
for (j = 0; j < m; j++) {
if (text[i + j] != pattern[j]) {
break;
}
}
if (j == m) {
return i; // 找到匹配
}
}
return -1; // 未找到
}
// 2. KMP算法:高效字符串匹配
void compute_lps(const char* pattern, int m, int* lps) {
int len = 0; // 最长前缀后缀长度
lps[0] = 0;
int i = 1;
while (i < m) {
if (pattern[i] == pattern[len]) {
len++;
lps[i] = len;
i++;
} else {
if (len != 0) {
len = lps[len - 1];
} else {
lps[i] = 0;
i++;
}
}
}
}
int kmp_search(const char* text, const char* pattern) {
int n = strlen(text);
int m = strlen(pattern);
int* lps = malloc(m * sizeof(int));
compute_lps(pattern, m, lps);
int i = 0; // text的索引
int j = 0; // pattern的索引
while (i < n) {
if (pattern[j] == text[i]) {
i++;
j++;
}
if (j == m) {
free(lps);
return i - j; // 找到匹配
} else if (i < n && pattern[j] != text[i]) {
if (j != 0) {
j = lps[j - 1];
} else {
i++;
}
}
}
free(lps);
return -1; // 未找到
}
// 3. 字符串编辑距离(Levenshtein距离)
int edit_distance(const char* str1, const char* str2) {
int m = strlen(str1);
int n = strlen(str2);
// 创建DP表
int** dp = malloc((m + 1) * sizeof(int*));
for (int i = 0; i <= m; i++) {
dp[i] = malloc((n + 1) * sizeof(int));
}
// 初始化边界条件
for (int i = 0; i <= m; i++) dp[i][0] = i;
for (int j = 0; j <= n; j++) dp[0][j] = j;
// 填充DP表
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (str1[i-1] == str2[j-1]) {
dp[i][j] = dp[i-1][j-1]; // 字符相同
} else {
int insert = dp[i][j-1] + 1;
int delete = dp[i-1][j] + 1;
int replace = dp[i-1][j-1] + 1;
dp[i][j] = (insert < delete) ?
((insert < replace) ? insert : replace) :
((delete < replace) ? delete : replace);
}
}
}
int result = dp[m][n];
// 清理内存
for (int i = 0; i <= m; i++) free(dp[i]);
free(dp);
return result;
}
五、数据结构相关算法
5.1 链表算法
typedef struct Node {
int data;
struct Node* next;
} Node;
// 1. 链表反转(迭代法)
Node* reverse_list_iterative(Node* head) {
Node* prev = NULL;
Node* current = head;
Node* next = NULL;
while (current != NULL) {
next = current->next; // 保存下一个节点
current->next = prev; // 反转指针
prev = current; // 移动prev
current = next; // 移动current
}
return prev; // 新的头节点
}
// 2. 链表反转(递归法)
Node* reverse_list_recursive(Node* head) {
if (head == NULL || head->next == NULL) {
return head;
}
Node* new_head = reverse_list_recursive(head->next);
head->next->next = head;
head->next = NULL;
return new_head;
}
// 3. 检测链表环(Floyd判圈算法)
int has_cycle(Node* head) {
if (head == NULL || head->next == NULL) {
return 0;
}
Node* slow = head;
Node* fast = head;
while (fast != NULL && fast->next != NULL) {
slow = slow->next; // 每次走一步
fast = fast->next->next; // 每次走两步
if (slow == fast) {
return 1; // 有环
}
}
return 0; // 无环
}
// 4. 合并两个有序链表
Node* merge_sorted_lists(Node* l1, Node* l2) {
// 创建哑节点简化代码
Node dummy;
Node* tail = &dummy;
dummy.next = NULL;
while (l1 != NULL && l2 != NULL) {
if (l1->data <= l2->data) {
tail->next = l1;
l1 = l1->next;
} else {
tail->next = l2;
l2 = l2->next;
}
tail = tail->next;
}
// 连接剩余部分
tail->next = (l1 != NULL) ? l1 : l2;
return dummy.next;
}
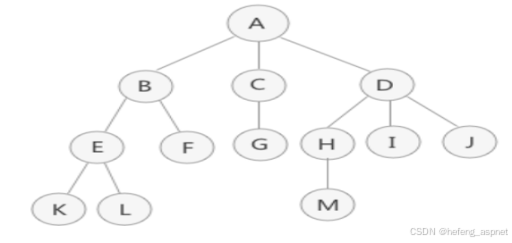
5.2 树算法
typedef struct TreeNode {
int value;
struct TreeNode* left;
struct TreeNode* right;
} TreeNode;
// 1. 二叉树遍历(递归版)
void inorder_traversal(TreeNode* root) {
if (root == NULL) return;
inorder_traversal(root->left);
printf("%d ", root->value);
inorder_traversal(root->right);
}
void preorder_traversal(TreeNode* root) {
if (root == NULL) return;
printf("%d ", root->value);
preorder_traversal(root->left);
preorder_traversal(root->right);
}
void postorder_traversal(TreeNode* root) {
if (root == NULL) return;
postorder_traversal(root->left);
postorder_traversal(root->right);
printf("%d ", root->value);
}
// 2. 二叉树遍历(迭代版,使用栈)
void inorder_iterative(TreeNode* root) {
TreeNode* stack[100];
int top = -1;
TreeNode* current = root;
while (current != NULL || top != -1) {
// 遍历到最左节点
while (current != NULL) {
stack[++top] = current;
current = current->left;
}
// 弹出并访问
current = stack[top--];
printf("%d ", current->value);
// 转向右子树
current = current->right;
}
}
// 3. 二叉树高度计算
int tree_height(TreeNode* root) {
if (root == NULL) {
return 0;
}
int left_height = tree_height(root->left);
int right_height = tree_height(root->right);
return (left_height > right_height ? left_height : right_height) + 1;
}
// 4. 二叉树镜像(反转)
void mirror_tree(TreeNode* root) {
if (root == NULL) return;
// 交换左右子树
TreeNode* temp = root->left;
root->left = root->right;
root->right = temp;
// 递归处理子树
mirror_tree(root->left);
mirror_tree(root->right);
}
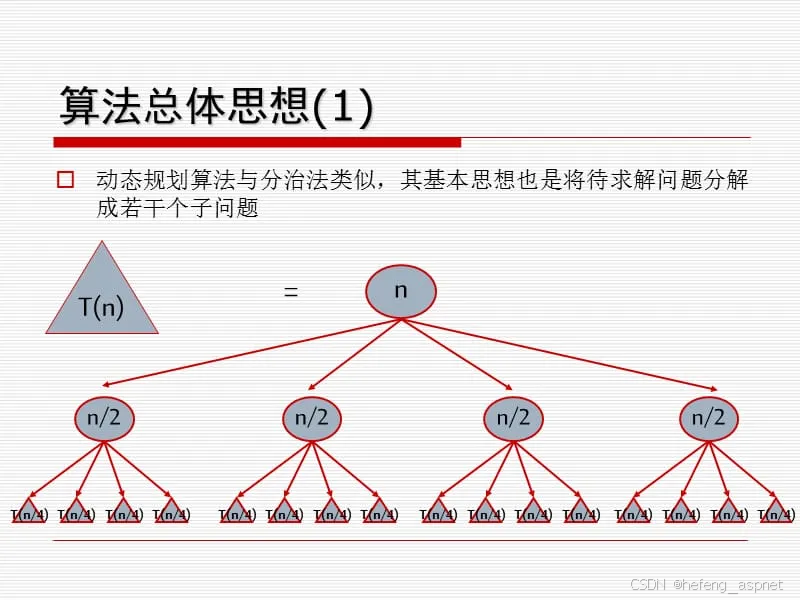
六、动态规划算法
6.1 经典DP问题
// 1. 斐波那契数列(带记忆化)
long long fibonacci(int n, long long* memo) {
if (n <= 1) return n;
if (memo[n] != -1) return memo[n];
memo[n] = fibonacci(n-1, memo) + fibonacci(n-2, memo);
return memo[n];
}
// 2. 0-1背包问题
int knapsack(int capacity, int weights[], int values[], int n) {
int** dp = malloc((n + 1) * sizeof(int*));
for (int i = 0; i <= n; i++) {
dp[i] = malloc((capacity + 1) * sizeof(int));
}
// 初始化
for (int i = 0; i <= n; i++) {
for (int w = 0; w <= capacity; w++) {
if (i == 0 || w == 0) {
dp[i][w] = 0;
} else if (weights[i-1] <= w) {
int include = values[i-1] + dp[i-1][w - weights[i-1]];
int exclude = dp[i-1][w];
dp[i][w] = (include > exclude) ? include : exclude;
} else {
dp[i][w] = dp[i-1][w];
}
}
}
int result = dp[n][capacity];
// 清理内存
for (int i = 0; i <= n; i++) free(dp[i]);
free(dp);
return result;
}
// 3. 最长公共子序列(LCS)
int lcs(const char* str1, const char* str2) {
int m = strlen(str1);
int n = strlen(str2);
int** dp = malloc((m + 1) * sizeof(int*));
for (int i = 0; i <= m; i++) {
dp[i] = malloc((n + 1) * sizeof(int));
}
for (int i = 0; i <= m; i++) {
for (int j = 0; j <= n; j++) {
if (i == 0 || j == 0) {
dp[i][j] = 0;
} else if (str1[i-1] == str2[j-1]) {
dp[i][j] = dp[i-1][j-1] + 1;
} else {
dp[i][j] = (dp[i-1][j] > dp[i][j-1]) ?
dp[i-1][j] : dp[i][j-1];
}
}
}
int result = dp[m][n];
// 清理内存
for (int i = 0; i <= m; i++) free(dp[i]);
free(dp);
return result;
}
6.2 路径规划算法
// Floyd-Warshall算法:所有顶点对的最短路径
#define INF 99999
#define V 4 // 顶点数
void floyd_warshall(int graph[V][V]) {
int dist[V][V];
// 初始化距离矩阵
for (int i = 0; i < V; i++) {
for (int j = 0; j < V; j++) {
dist[i][j] = graph[i][j];
}
}
// 动态规划核心
for (int k = 0; k < V; k++) {
for (int i = 0; i < V; i++) {
for (int j = 0; j < V; j++) {
if (dist[i][k] + dist[k][j] < dist[i][j]) {
dist[i][j] = dist[i][k] + dist[k][j];
}
}
}
}
// 打印结果
printf("最短距离矩阵:\n");
for (int i = 0; i < V; i++) {
for (int j = 0; j < V; j++) {
if (dist[i][j] == INF) {
printf("INF\t");
} else {
printf("%d\t", dist[i][j]);
}
}
printf("\n");
}
}
希望以上内容对你有帮助。
如果您喜欢此文章,请收藏、点赞、评论,谢谢,祝您快乐每一天。