Gram矩阵（Gram matrix）是一个数学工具，常用于线性代数、机器学习和图像处理中。它本质上是一个"相似度表格"，用来描述一组向量（或数据点）之间两两的相似程度。咱们用日常生活比喻来讲解，避开复杂公式，先抓本质。
1. 基本想法：向量像"人"，Gram矩阵像"朋友圈相似度表"
- 想象你有几个朋友（对应"向量"），每个朋友有自己的特征，比如身高、体重、性格分数等（这些是向量的"维度"）。
- 你想知道他们之间谁和谁更"相似"？可以用"内积"（dot product）来衡量：两个朋友的特征值相乘再加起来，得分越高越相似（比如都高个子、都外向，得分就高）。
- Gram矩阵就是一个表格：行和列都对应这些朋友，表格里的每个格子填的就是他们俩的相似度分数。
- 对角线：每个朋友和自己的相似度（总是正的，代表"强度"）。
- 非对角线：不同朋友间的相似度（可能正、负或零，表示相似、相反或无关）。
2. 怎么计算？（简单步骤）
- 假设你有一组向量，放在一个矩阵V里（每列一个向量）。
- Gram矩阵G = V转置（
） × V（矩阵乘法）。
- "转置"就是把行变列（像把表格翻转90度）。
- 乘法结果的每个元素
- 如果向量是行向量，就
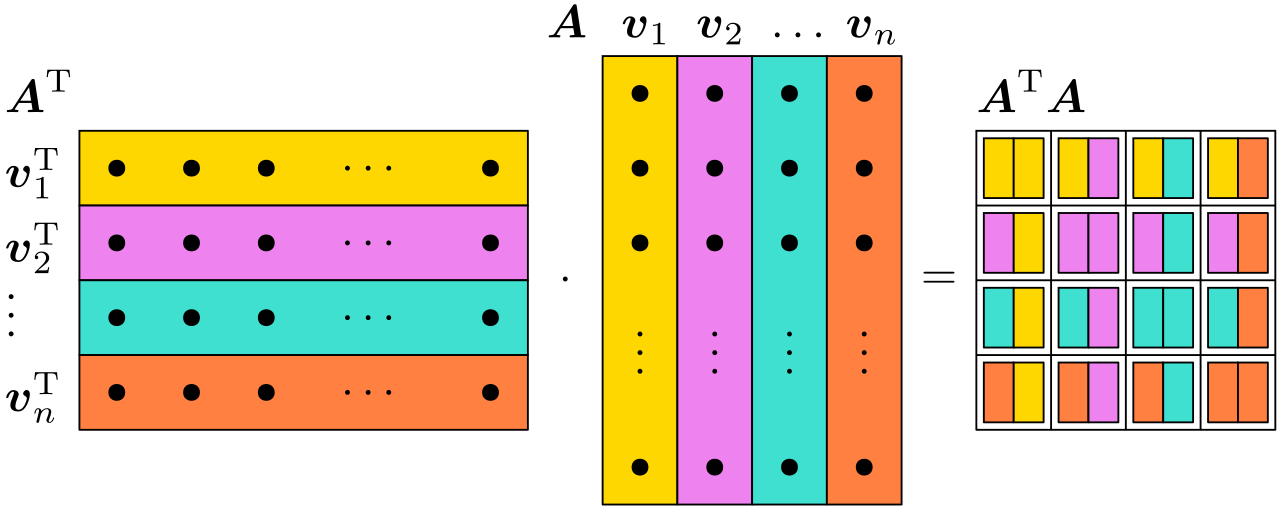
这张图其实把格拉姆矩阵 （Gram matrix）= "两两做内积的表格"画得很直观：
1）先读图：它在做什么乘法？
图里中间那根彩色"竖条"矩阵写着 A，它的列是
左边是 ，也就是把这些列向量转成行向量：
然后图在算：
2）为什么 就是"格拉姆矩阵"？
矩阵乘法的第 (i,j) 个元素，是"第 i 行"点乘"第 j 列"。
在这里：
-
-
A 的第 j 列就是
所以
这句话就是格拉姆矩阵的定义：
Gram 矩阵 G 的元素
图右侧那一格格小方块，就是把所有 和
两两"点一下"，填成一张表。
3）每个格子在"几何上"是什么意思？
记住内积的几何意义：
所以格拉姆矩阵每一格都在回答一个问题：这两根向量有多"同向/相似"？
-
对角线
就是每根向量自己的"长度平方"。
图里对角线方块颜色"很纯"（同色），表示"自己和自己匹配度最大"。
-
非对角
-
若
这格就"很弱/接近空白"（相似度为 0）。
-
若夹角小、同向，cosθ>0 ⇒
这格就"大"（相似）。
-
若反向，cosθ<0 ⇒
-
你可以把右边那张矩阵当作："向量相似度热力图（但用内积计量）"。
4）格拉姆矩阵有哪些关键性质（机器学习里很常用）？
设 ：
-
对称 ：
因为
-
半正定（PSD）：对任意 x，都有
这点非常重要：很多优化问题靠它保证"碗状凸性"。
-
秩不超过维度 ：
如果每个
这意味着：就算你有很多向量，它们的"独立信息"也被空间维度限制。
5）它在机器学习里常出现在哪？
-
线性回归 / 最小二乘 ：经典的
-
核方法 / SVM ：把内积换成核函数
-
相似度矩阵：用点积/余弦相似度衡量样本之间的接近程度
-
PCA/协方差相关 ：中心化后
我们就用一个带具体数字 的小例子，把图里的"点点（内积）"彻底算清楚------你会直观看到：右边那张方格表就是把每两根列向量都"点乘"一遍。
1）造一个和图一致的场景：A 的列就是 4 根向量
设 A 有 4 列（对应图里 4 种颜色的竖条），每列是一个 2 维向量：
把它们并排放成矩阵：
2）格拉姆矩阵 ：每个格子就是一个"内积"
我们把所有两两内积都算出来（这就是右侧方格表每个格子的数）：
先算对角线（自己点自己 = 长度平方）
再算非对角线（两两相似度）
于是整张"方格表"（Gram 矩阵）就是：
你看它天然就对称 （因为 ）：左下角就是右上角的镜像------这也和图的方格"左右对称感"一致。
3）把每个数翻译成几何含义：同向、正交、反向
内积和角度关系：
所以：
-
g13=0 ⇒ v1 与 v3 正交（90°）
-
g14=−1<0 ⇒ v1 与 v4 偏反向（钝角）
-
g12=1>0 ⇒ v1 与 v2 偏同向（锐角）
我们甚至能算出角度（用余弦）：
所以 Gram 矩阵就是"角度 + 长度"的编码表 ：
对角线管长度，非对角线管夹角（方向相似度）。
4）为什么机器学习里爱用它？一句话就够
如果把 当成样本（或特征向量），那么 G 就是：
样本两两相似度矩阵（用内积做相似度）
-
在线性回归里：
-
在核方法里：把内积换成
图中**"点最多"**其实是在强调：每个向量里有很多个分量 （图里用一串黑点 + 省略号表示），而 Gram 矩阵里的一个格子 ，就是把这"一长串点"逐个相乘再全部相加得到的。
我就拿图里最典型的那个格子------左上角 g11 （黄色行 × 黄色列，也就是 和 v1）来示范：这格对应的"点"（分量）最多、最直观。
1）把图里的"点点"写成符号
图中黄色那行是：
意思是：v1 有很多个分量。把它写成具体形式就是：
这里每个 就对应图里的一颗黑点（省略号表示中间还有很多颗）。
2）"一个格子"是怎么来的：逐点相乘 + 全部相加
右侧 Gram 矩阵 的左上角格子是：
按"点乘"的规则：
也就是：
这就是为什么对角线是"长度平方"：因为自己跟自己点乘，就是"每个点自己乘自己，再求和"。
3）同理，右上角那种"双色格子"是怎么来的？
比如第一行第三列那个格子（黄色行 × 青色列）：
如果
那么：
你可以把它想成：
同一"高度"的点配对相乘（第 1 个点乘第 1 个点，第 2 个点乘第 2 个点......），最后把所有乘积加起来，塞进那个格子。
图里用"双色"表示：这个格子来自"黄色那行的向量"和"青色那列的向量"的配对。
4）一句话把图讲透
-
左边：很多行
-
中间：很多列
-
右边：每个格子
下面我们来把第一行完全展开成"第1点×第1点 + 第2点×第2点 + ......"的形式，和图里的颜色位置一一对应。
"第一行"在图里就是：最上面那条（黄色那条）行向量 ，去和中间矩阵 A 的每一列 依次"点乘"，得到右侧 Gram 矩阵的第一行。
1）先把第一行写成公式：第一行 = v1 和所有列两两内积
设
那么 Gram 矩阵第一行就是：
也就是：
-
第 1 个格子：
-
第 2 个格子：
-
...
-
第 n 个格子：
2）把"点最多"的意思展开：每个格子都是"一长串点逐个相乘再相加"
假设每个向量有 m 个分量（图里黑点很多 + 省略号）：
那么第一行第 j 列的格子：
这句话对应图里的动作就是：
黄色那一行的第 1 个点 × 第 j 列的第 1 个点
+ 黄色那一行的第 2 个点 × 第 j 列的第 2 个点
+ ...（一直配对到最后一个点）
3）第一行里最特殊的那个格子：第一个 g11
第一行第一个格子（黄色×黄色）：
所以第一行的第一个格子永远是"黄色向量的长度平方"，通常也会是这一行里最"显眼/大"的值之一（图上常用更强的视觉强调来画对角线）。
4）用 3 个点做一个"微缩版"，你会秒懂第一行怎么填
把"很多点"先缩成 3 个点（只是演示规则）：
那么第一行就是：
把 3 换成 m，就是图里"点最多"的真实情况。
注意点（避免坑）
- Gram矩阵总是方形、对称、正半定（数学上保证它"稳定"）。
- 如果向量是归一化的（长度1），它就类似相关系数矩阵（-1到1）。
- 在编程中，用NumPy超简单：G = np.dot(V.T, V)。