Python数据结构（四）：栈详解

本文是Python数据结构系列的第四篇，我们将深入探讨栈的概念、特点、操作及Python实现。栈是一种后进先出（LIFO）的数据结构，广泛应用于函数调用、表达式求值、括号匹配等场景。

一、栈的基本概念

栈（Stack）又名堆栈，它是一种运算受限的线性表，是一种容器，可存入数据元素、访问元素、删除元素。它的特点在于只能允许在容器的一端（称为栈顶top）进行存入数据（push）和输出数据（pop）的运算，没有位置概念，保证任何时候都可以访问、删除元素。

栈仅允许在栈顶一端进行操作，因此，栈是按照**先进后出（LIFO，Last In First Out）**的原理进行运作。

栈的示意图：

复制代码

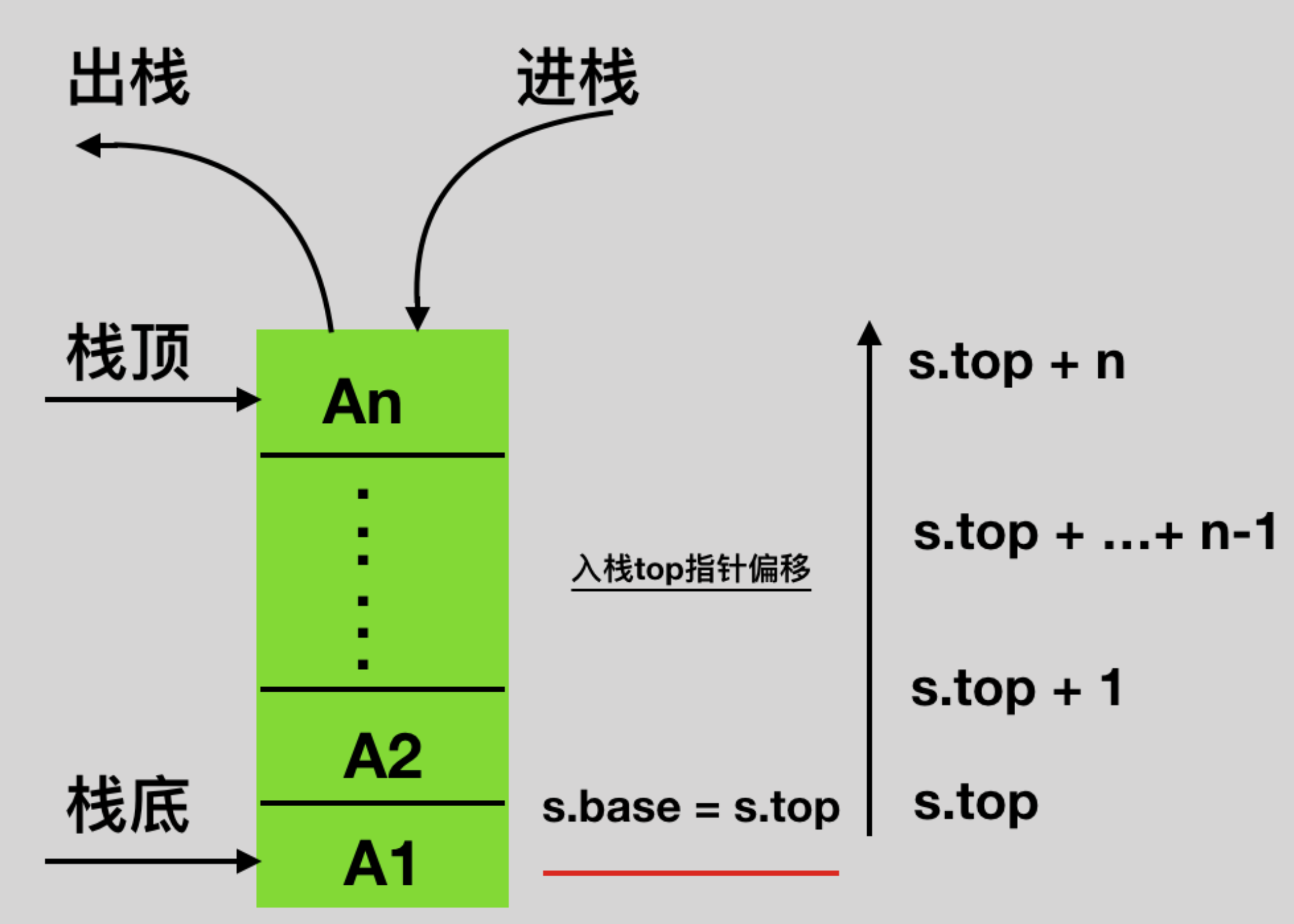
    栈顶
    ↓
|  data4  | ← 最后进入，最先出去
|  data3  |
|  data2  |
|  data1  | ← 最先进入，最后出去
 ---------
    栈底

或

栈的操作限制：

入栈（push）：只能在栈顶添加元素
出栈（pop）：只能从栈顶移除元素
查看栈顶（peek）：只能查看栈顶元素

二、Python中栈的实现

Python中可以使用列表（list）来实现栈，因为列表的append()和pop()方法天然符合栈的操作特性。

2.1 栈类的框架

python 复制代码

class Stack:
    """栈"""
    
    def __init__(self):
        """构造容器，不希望外部可以操作这个列表，所以构造私有属性"""
        self.__list = []
    
    def push(self, data):
        """添加一个新元素，压入栈顶"""
        self.__list.append(data)
    
    def pop(self):
        """弹出一个栈顶的元素（移除且返回）"""
        if not self.is_empty():
            return self.__list.pop()
        else:
            return None  # 或者抛出异常
    
    def peek(self):
        """返回栈顶元素，不移除元素"""
        if self.__list:
            return self.__list[-1]
        else:
            return None
    
    def is_empty(self):
        """判断栈是否为空"""
        return self.__list == []
    
    def size(self):
        """返回栈的元素个数"""
        return len(self.__list)

三、栈的操作

栈支持以下基本操作：

方法名	功能描述
`push(data)`	将数据压入栈顶
`pop()`	将栈顶数据移除并返回（栈被修改）
`peek()`	查看栈顶元素，但未弹出
`is_empty()`	检查栈是否为空
`size()`	获取栈的大小

3.1 入栈操作（push）

python 复制代码

def push(self, data):
    """添加一个新元素，压入栈顶"""
    self.__list.append(data)

3.2 出栈操作（pop）

python 复制代码

def pop(self):
    """弹出一个栈顶的元素（移除且返回）"""
    if not self.is_empty():
        return self.__list.pop()
    else:
        return None  # 栈为空时返回None

3.3 查看栈顶元素（peek）

python 复制代码

def peek(self):
    """返回栈顶元素，不移除元素"""
    if self.__list:
        return self.__list[-1]
    else:
        return None

3.4 判断栈是否为空

python 复制代码

def is_empty(self):
    """判断栈是否为空"""
    return self.__list == []

3.5 获取栈的大小

python 复制代码

def size(self):
    """返回栈的元素个数"""
    return len(self.__list)

四、栈的应用示例

python 复制代码

if __name__ == "__main__":
    stack = Stack()
    
    # 判断栈是否为空
    print(stack.is_empty())  # True
    
    # 入栈操作
    stack.push(0)  # 栈：[0]
    stack.push(1)  # 栈：[0, 1]
    stack.push(2)  # 栈：[0, 1, 2]
    stack.push(3)  # 栈：[0, 1, 2, 3]
    
    # 获取栈的大小
    print(f'栈的长度：{stack.size()}')  # 4
    
    # 查看栈顶元素
    print(f'查看栈顶元素：{stack.peek()}')  # 3
    
    # 出栈操作
    print(f'弹出栈顶元素：{stack.pop()}')  # 3
    print(f'栈的长度：{stack.size()}')  # 3
    
    # 继续出栈
    print(f'弹出栈顶元素：{stack.pop()}')  # 2
    print(f'弹出栈顶元素：{stack.pop()}')  # 1
    print(f'弹出栈顶元素：{stack.pop()}')  # 0
    
    # 判断栈是否为空
    print(f'判断是否为空栈：{stack.is_empty()}')  # True
    
    # 尝试从空栈弹出元素
    print(f'弹出栈顶元素：{stack.pop()}')  # None

五、栈的实际应用场景

5.1 函数调用栈

在程序执行过程中，函数的调用和返回就是通过栈来管理的：

当函数被调用时，其状态（返回地址、局部变量等）被压入栈中
当函数返回时，从栈顶弹出状态信息，恢复调用者的执行环境

python 复制代码

def function_a():
    print("进入函数A")
    function_b()
    print("离开函数A")

def function_b():
    print("进入函数B")
    function_c()
    print("离开函数B")

def function_c():
    print("进入函数C")
    print("离开函数C")

function_a()

调用栈的变化：

复制代码

调用function_a() → 压入A
调用function_b() → 压入B
调用function_c() → 压入C
function_c()返回 → 弹出C
function_b()返回 → 弹出B
function_a()返回 → 弹出A

5.2 括号匹配检查

栈可以用来检查表达式中的括号是否匹配：

python 复制代码

def is_balanced_parentheses(expression):
    """检查括号是否匹配"""
    stack = Stack()
    mapping = {')': '(', ']': '[', '}': '{'}
    
    for char in expression:
        if char in '([{':
            # 左括号入栈
            stack.push(char)
        elif char in ')]}':
            # 右括号检查
            if stack.is_empty() or stack.pop() != mapping[char]:
                return False
    
    return stack.is_empty()

# 测试
print(is_balanced_parentheses("((()))"))  # True
print(is_balanced_parentheses("(()"))     # False
print(is_balanced_parentheses("([{}])"))  # True

5.3 表达式求值

栈可以用于中缀表达式转后缀表达式，以及后缀表达式的求值：

python 复制代码

def evaluate_postfix(expression):
    """计算后缀表达式"""
    stack = Stack()
    
    for token in expression.split():
        if token.isdigit():
            # 操作数入栈
            stack.push(int(token))
        else:
            # 操作符：弹出两个操作数，计算结果入栈
            right = stack.pop()
            left = stack.pop()
            
            if token == '+':
                result = left + right
            elif token == '-':
                result = left - right
            elif token == '*':
                result = left * right
            elif token == '/':
                result = left / right
            else:
                raise ValueError(f"未知操作符: {token}")
            
            stack.push(result)
    
    return stack.pop()

# 测试：计算 "3 4 + 5 *" 相当于 (3+4)*5
print(evaluate_postfix("3 4 + 5 *"))  # 35

六、栈的优缺点

优点：

操作简单：只允许在栈顶进行操作，实现简单
高效访问：栈顶元素的访问、插入、删除都是O(1)时间复杂度
内存管理简单：不需要维护额外的指针或索引
天然支持递归：函数调用栈是递归实现的基础

缺点：

访问受限：只能访问栈顶元素，不能随机访问其他元素
容量限制：基于数组实现的栈有固定大小限制（但Python列表可动态扩容）
可能溢出：递归过深或元素过多可能导致栈溢出

七、栈的不同实现方式

7.1 基于列表的实现（如上面所示）

使用Python内置列表
利用append()和pop()方法
简单直观，但可能需要动态扩容

7.2 基于链表的实现

可以使用单链表实现
链表头作为栈顶
入栈和出栈都是O(1)时间复杂度

python 复制代码

class Node:
    """链表节点"""
    def __init__(self, data):
        self.data = data
        self.next = None

class LinkedStack:
    """基于链表的栈"""
    def __init__(self):
        self.top = None
        self._size = 0
    
    def push(self, data):
        """入栈"""
        new_node = Node(data)
        new_node.next = self.top
        self.top = new_node
        self._size += 1
    
    def pop(self):
        """出栈"""
        if self.is_empty():
            return None
        data = self.top.data
        self.top = self.top.next
        self._size -= 1
        return data
    
    def peek(self):
        """查看栈顶"""
        return self.top.data if self.top else None
    
    def is_empty(self):
        """判断是否为空"""
        return self.top is None
    
    def size(self):
        """获取大小"""
        return self._size

总结

栈是一种简单但功能强大的数据结构，它的LIFO特性使其在多种场景下都非常有用。理解栈的原理和实现，对于掌握更复杂的算法和数据结构至关重要。

在实际开发中，栈的应用非常广泛：

编译器：语法分析、表达式求值
操作系统：函数调用、中断处理
浏览器：前进后退功能
文本编辑器：撤销操作
算法：深度优先搜索、回溯算法

虽然Python的列表已经可以很好地模拟栈的操作，但理解栈的抽象概念和实现原理，对于培养良好的算法思维和解决实际问题能力非常重要。

在下一篇中，我们将探讨队列（Queue），这是一种先进先出（FIFO）的数据结构，广泛应用于任务调度、消息传递等场景。

注意：本文是Python数据结构系列的第四篇，重点讲解栈的基本概念和实现。在实际编程中，虽然可以直接使用Python列表作为栈，但封装成专门的栈类可以提供更好的抽象和错误处理。理解栈的原理对于学习更高级的数据结构和算法至关重要。