控制系统建模仿真（四）：线性控制系统的数学模型

前言

欢迎进入第四章：线性控制系统的数学模型。在第一章中我们完成了"看房子"的整体概览，第二章我们夯实了"打地基"的编程基础，第三章我们掌握了解决科学运算问题的"专业工具箱"。如果说前三章是让你学会了如何操作工具，那么从本章开始，我们将真正进入控制系统的核心地带。

如果把控制系统设计比作一场建筑工程，那么第四章的任务就是**"绘制蓝图"**。在控制工程中，如果你无法用数学语言准确地描述你的受控对象，那么后续的稳定性分析、时域响应预测以及控制器设计都将是空中楼阁。

本章我们将学习如何将复杂的物理系统抽象为 MATLAB 能够理解的数学"画像"------无论是经典的传递函数（Transfer Function）、直观的零极点增益（ZPK），还是现代控制理论核心的状态空间（State Space）。只有拿到了这些"原材料"，我们才能在后续章节中对系统进行全方位的打磨与控制。

如果没有学过前三篇内容，建议通系列链接进行复习，以便更好地理解本章的模型构建逻辑。

---

一、 核心原理与知识点汇总

1. 三种基本模型表现形式 ：
   • 传递函数形式 (TF)：基于拉普拉斯变换，适用于单输入单输出（SISO）系统。
   • 状态空间形式 (SS)：现代控制理论核心，适用于多输入多输出（MIMO）系统。
   • 零极点增益形式 (ZPK)：通过根的分布直观观察系统稳定性。
2. 连续与离散转换：真实物理系统多为连续，但控制器多为数字（离散）实现。
3. 结构图化简：将复杂的串联、并联、反馈系统合并为一个总的传递函数。
4. 模型降阶：用简单的低阶模型去近似复杂的高阶模型。

---

二、 必会函数清单与实例演示

1. tf() ------ 创建传递函数模型

• 功能说明：利用分子和分母的多项式系数定义系统的传递函数。

• 输入定义 ：num（分子系数向量），den（分母系数向量）。

• 返回值：传递函数对象（TF object）。

• 代码示例 ：

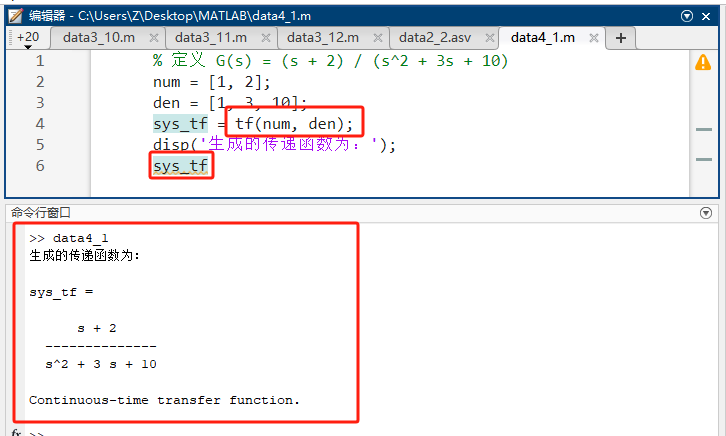
  % 定义 G(s) = (s + 2) / (s^2 + 3s + 10)
  num = [1, 2];
  den = [1, 3, 10];
  sys_tf = tf(num, den);
  disp('生成的传递函数为：');
  sys_tf

• 源码讲解 ：系数向量按 sss 的降幂排列。[1, 2] 代表 1s+21s + 21s+2。

• 预期输出 ：显示漂亮的数学分式 G(s)G(s)G(s)。
  

2. ss() ------ 创建状态空间模型

• 功能说明 ：根据状态方程矩阵 A,B,C,DA, B, C, DA,B,C,D 定义系统。

• 输入定义 ：矩阵 AAA（系统阵）, BBB（输入阵）, CCC（输出阵）, DDD（直接传导阵）。

• 返回值：状态空间对象（SS object）。

• 代码示例 ：

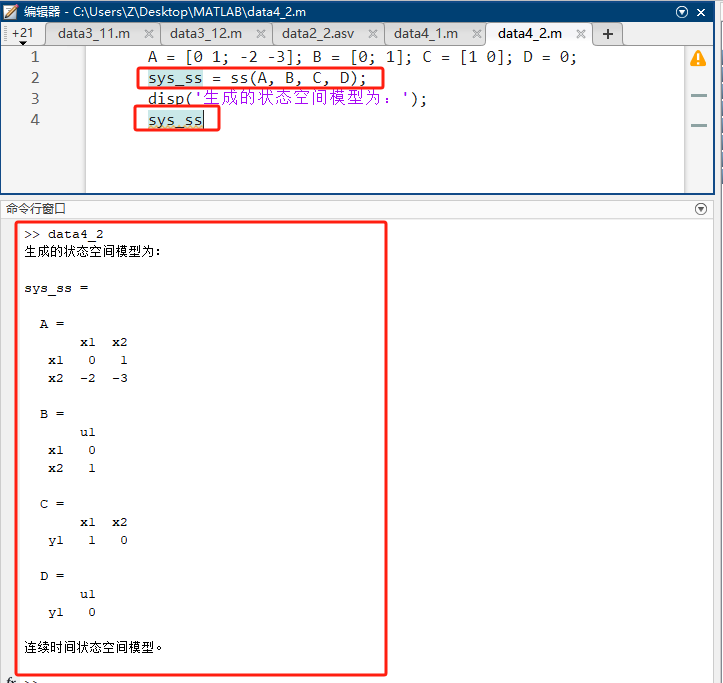
  A = [0 1; -2 -3]; B = [0; 1]; C = [1 0]; D = 0;
  sys_ss = ss(A, B, C, D);
  disp('生成的状态空间模型为：');
  sys_ss

• 源码讲解：直接将微分方程组转化为矩阵形式输入。

• 预期输出 ：显示 A,B,C,DA, B, C, DA,B,C,D 各矩阵的值。
  

3. zpk() ------ 创建零极点增益模型

• 功能说明：通过指定系统的零点、极点和增益来建立模型。

• 输入定义 ：z（零点向量）, p（极点向量）, k（标量增益）。

• 返回值：ZPK 对象。

• 代码示例 ：

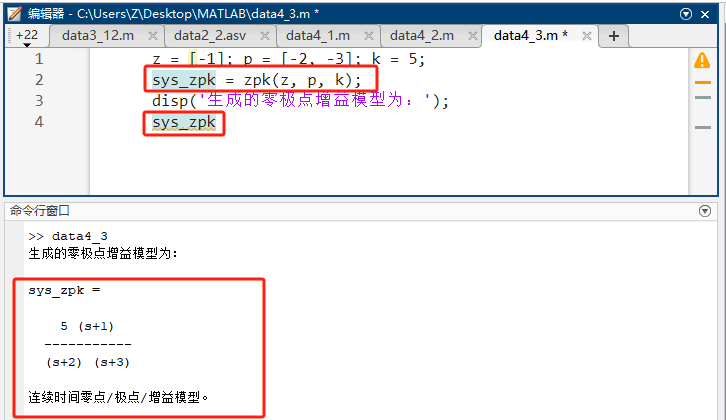
  z = [-1]; p = [-2, -3]; k = 5;
  sys_zpk = zpk(z, p, k);
  disp('生成的零极点增益模型为：');
  sys_zpk

• 源码讲解：该形式最能体现稳定性（极点都在左半平面）。

• 预期输出 ：5(s+1)/((s+2)(s+3))5(s+1) / ((s+2)(s+3))5(s+1)/((s+2)(s+3))。
  

4. c2d() ------ 连续系统转离散系统

• 功能说明 ：将 sss 域模型转换为数字控制所需的 zzz 域离散模型。

• 输入定义 ：连续系统对象 sys, 采样时间 Ts。

• 返回值：离散系统对象。

• 代码示例 ：

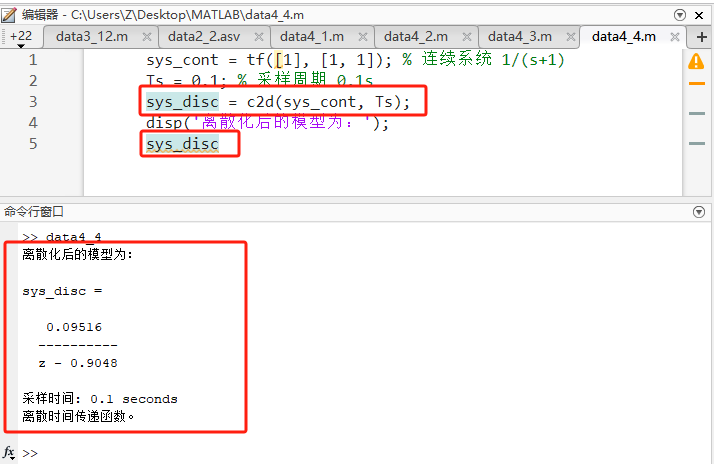
  sys_cont = tf([1], [1, 1]); % 连续系统 1/(s+1)
  Ts = 0.1; % 采样周期 0.1s
  sys_disc = c2d(sys_cont, Ts);
  disp('离散化后的模型为：');
  sys_disc

• 源码讲解：默认采用零阶保持器（ZOH）进行转换。

• 预期输出 ：一个关于 zzz 的传递函数。
  

5. feedback() ------ 系统反馈连接

• 功能说明：计算闭环控制系统的总传递函数。

• 输入定义 ：sys1（前向通路）, sys2（反馈通路，默认为单位反馈）。

• 返回值：闭环系统对象。

• 代码示例 ：

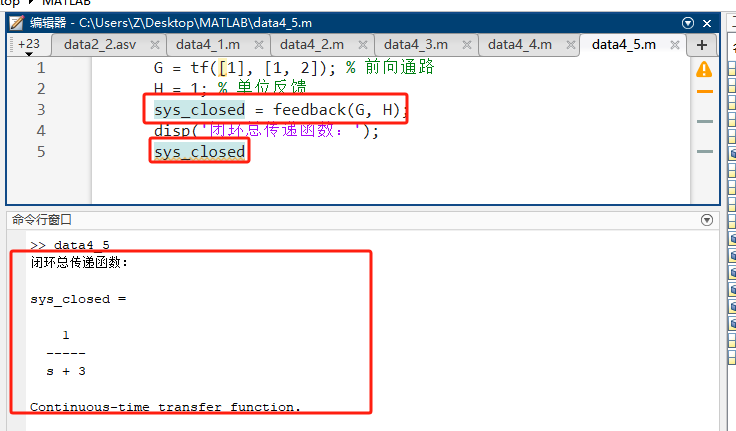
  G = tf([1], [1, 2]); % 前向通路
  H = 1; % 单位反馈
  sys_closed = feedback(G, H);
  disp('闭环总传递函数：');
  sys_closed

• 源码讲解 ：实现公式 G/(1+GH)G / (1 + GH)G/(1+GH)，如果最后加个参数 -1 可表示正反馈。

• 预期输出 ：化简后的闭环传递函数。
  

6. minreal() ------ 最小实现（消除零极点对）

• 功能说明：自动约去分子分母中相同或极接近的零极点项。

• 代码示例 ：

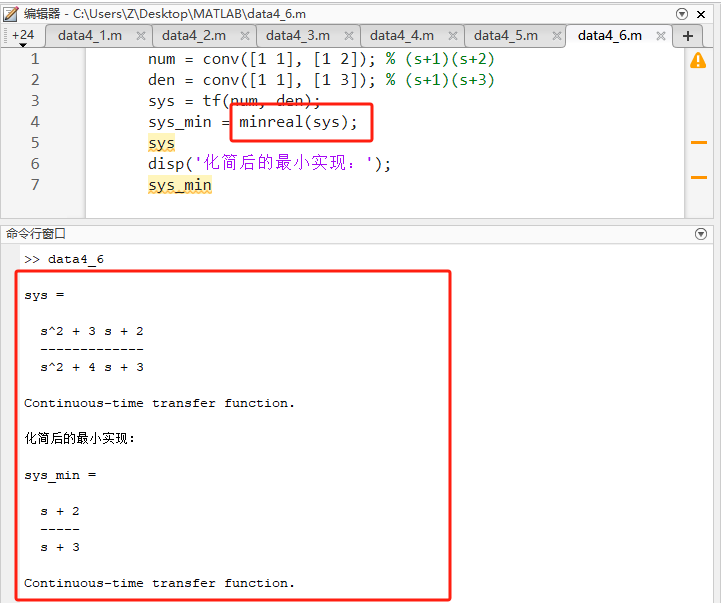
  num = conv([1 1], [1 2]); % (s+1)(s+2)
  den = conv([1 1], [1 3]); % (s+1)(s+3)
  sys = tf(num, den);
  sys_min = minreal(sys);
  sys
  disp('化简后的最小实现：');
  sys_min

• 源码讲解 ：conv 用于多项式相乘。minreal 发现了分子分母都有 (s+1)(s+1)(s+1) 并将其消去。

• 预期输出 ：(s + 2) / (s + 3)。
  

---

三、语法知识：多项式处理

在控制系统建模中，我们经常需要处理形如 G(s)=num(s)den(s)G(s) = \frac{num(s)}{den(s)}G(s)=den(s)num(s) 的分式。而 num(s)num(s)num(s) 和 den(s)den(s)den(s) 通常是多个括号相乘（因式形式）或者是一串长长的多项式。

为了高效地建立模型，MATLAB 提供了专门处理多项式的"三剑客"：conv、roots 和 poly。以下是详细的示例与代码讲解：

---

1. conv(p1, p2) ------ 多项式相乘

• 原理 ：在数学中，多项式相乘对应于系数向量的卷积运算。
• 功能：计算两个多项式相乘后的系数。
• 场景 ：当你已知系统的各个环节（如：s+1s+1s+1 和 s+2s+2s+2），想求它们的乘积作为传递函数的分母时。

可执行例子：

% 目标：求 (s+1) * (s^2 + 3s + 2) 的系数
p1 = [1 1];          % 代表 1s + 1
p2 = [1 3 2];        % 代表 1s^2 + 3s + 2

p_result = conv(p1, p2); 

disp('相乘后的系数向量为：');
disp(p_result);

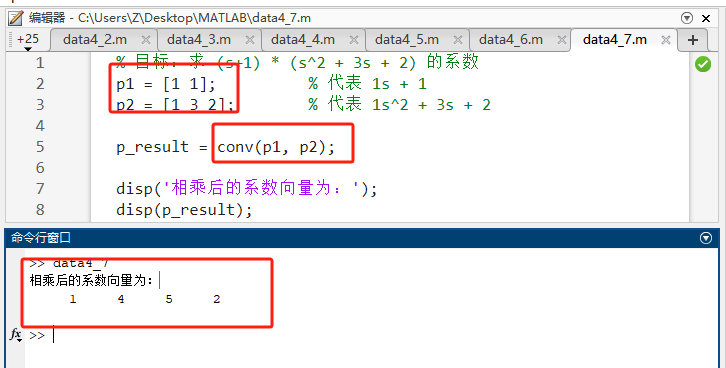
% 验证结果：手动计算应为 s^3 + 4s^2 + 5s + 2

• 源码讲解 ：输入参数是两个按 sss 的降幂排列的系数向量。返回的是相乘后新多项式的系数向量。
• 预期输出 ：1 4 5 2
  

---

2. roots(p) ------ 求多项式的根（找极点/零点）

• 原理 ：求解代数方程 P(s)=0P(s) = 0P(s)=0。
• 功能：输入多项式系数，返回所有的根。
• 场景 ：在控制理论中，分母多项式的根就是系统的极点，直接决定了系统是否稳定。

可执行例子：

% 目标：求多项式 s^2 + 5s + 6 = 0 的根
p = [1 5 6]; 

r = roots(p);

disp('该多项式的根（系统极点）为：');
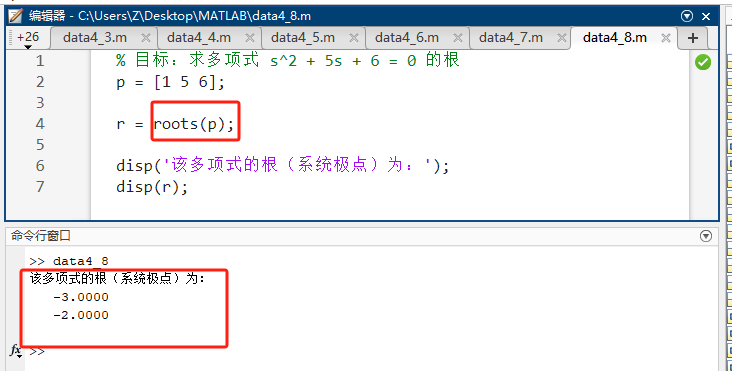
disp(r);

• 源码讲解 ：输入 p 是系数向量。返回的 r 是一个列向量，包含该方程所有的解。

• 预期输出 ：

  -3
  -2

---

3. poly(r) ------ 已知根求多项式（还原系数）

• 原理 ：它是 roots 的逆运算。已知 r1,r2...rnr_1, r_2...r_nr1,r2...rn，计算 (s−r1)(s−r2)...(s−rn)(s-r_1)(s-r_2)...(s-r_n)(s−r1)(s−r2)...(s−rn)。
• 功能：输入一组根，返回多项式的系数向量。
• 场景 ：当你设计了一个控制器，希望它的极点配置在 −1-1−1 和 −5-5−5 时，通过这个函数可以反求出分母多项式的系数。

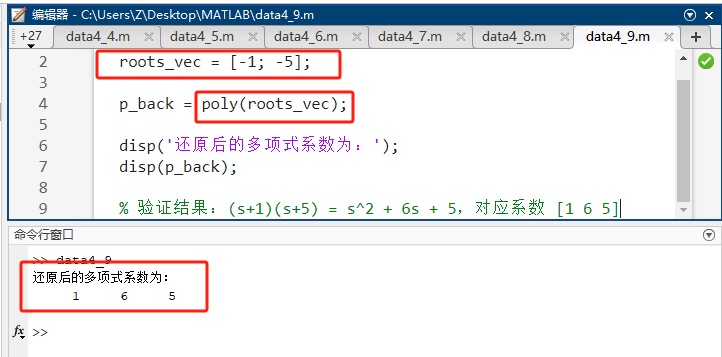
可执行例子：

% 目标：已知根为 -1 和 -5，求对应的多项式系数
roots_vec = [-1; -5];

p_back = poly(roots_vec);

disp('还原后的多项式系数为：');
disp(p_back);

% 验证结果：(s+1)(s+5) = s^2 + 6s + 5，对应系数 [1 6 5]

• 源码讲解 ：输入可以是行向量或列向量形式的根。注意，返回的系数向量第一个元素通常是 1（最高次项系数）。
• 预期输出 ：1 6 5
  

---

综合运用：建立一个复杂的传递函数

任务 ：建立 G(s)=5(s+1)(s+2)(s+3)(s+4)G(s) = \frac{5(s+1)}{(s+2)(s+3)(s+4)}G(s)=(s+2)(s+3)(s+4)5(s+1)

% 1. 处理分子
num = 5 * [1 1]; % 5s + 5

% 2. 处理分母：连续使用 conv
den = conv([1 2], [1 3]);    % 先算 (s+2)(s+3)
den = conv(den, [1 4]);      % 再乘 (s+4)

% 3. 生成模型
sys = tf(num, den);

disp('生成的系统模型为：');
sys

预期输出：

      5 s + 5
  -----------------------
  s^3 + 9 s^2 + 26 s + 24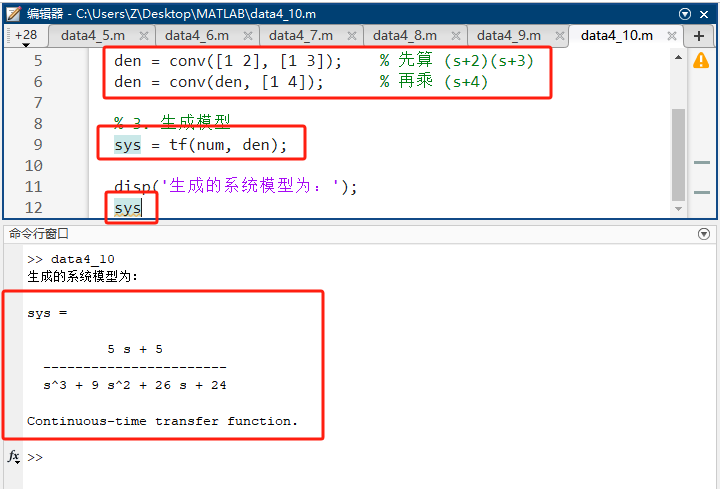

---

四、 第四章 关于 Simulink 的知识

在这一章中，你需要掌握如何把 MATLAB 定义的模型丢进 Simulink：

1. LTI System 模块 ：在 Simulink 中拖入这个模块，在参数栏直接填入你在 MATLAB 里定义的变量名（如 sys_tf）。
2. Transfer Fcn 模块 ：手动在参数框输入 [1, 2] 和 [1, 3, 10]。
3. 观察模型 ：使用 Scope 模块查看这些数学模型对阶跃信号的初步响应。

---

本章复习建议

关键实验 ：

请尝试将一个传递函数 tf 用 ss() 转换成状态空间，再用 tf() 转回来。

G = tf([1], [1, 2, 1]);
sys_ss = ss(G);  % 转状态空间
G_back = tf(sys_ss); % 转回传递函数

• 注意 ：有时候转回来会出现微小的数值余项（例如 10−1610^{-16}10−16），这时候配合使用 minreal() 效果更佳。