二叉搜索树 - 技术栈

概念

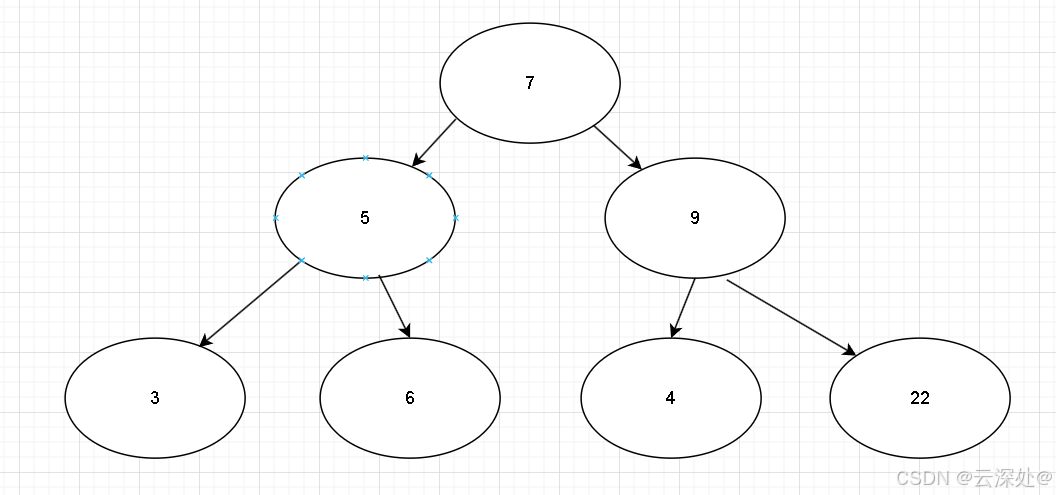
二叉搜索树又称二叉排序树 或者是一个空树

特点

左子树所有节点的值都小于根节点的值，右子树所有节点的值都大于根节点的值

它的左右子树也分别为二叉搜索树

解决了数组插入删除数据时的效率问题，并且衍生出AVL树，红黑树，B树系列

时间复杂度O(n)

格式

二叉搜索树的查找

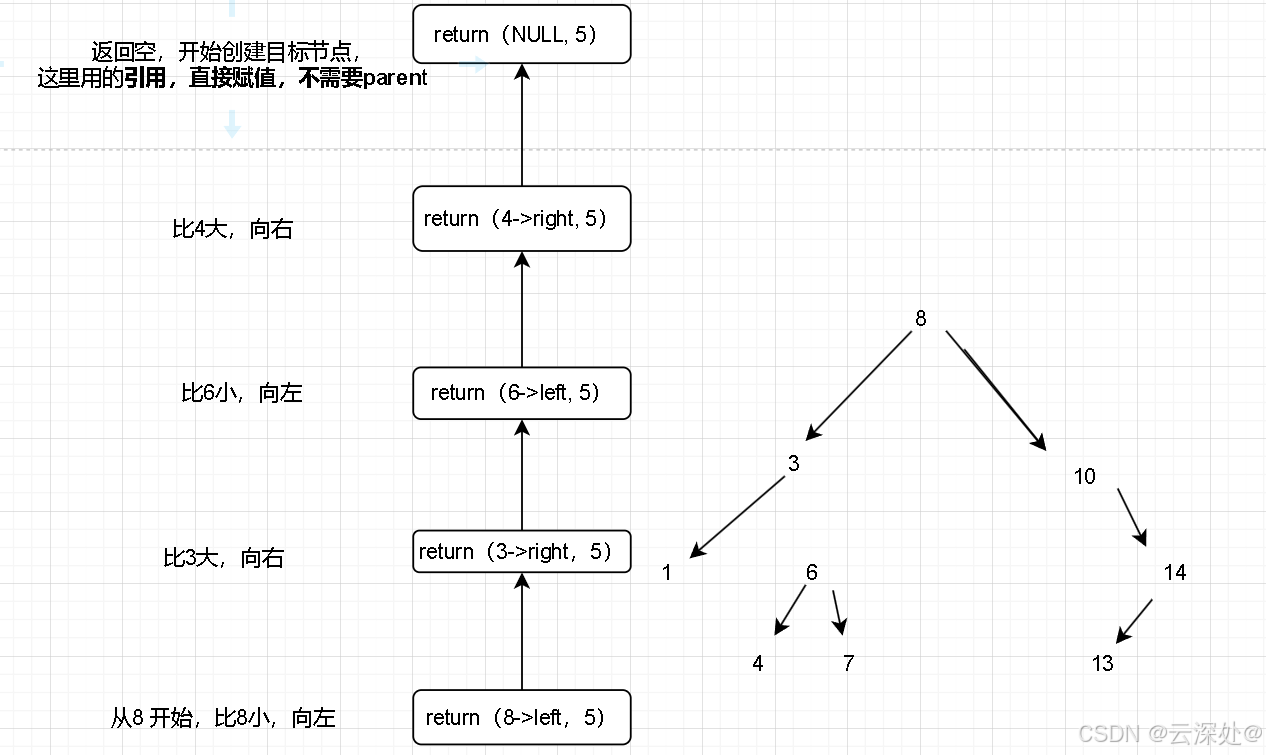
从根开始比较，查找，比根大向右边找，反之向左
最多查找高度次，若走到空，则值不存在

二叉查找树的插入

树为空，新增节点，赋值root
树不为空，查找+插入新节点

二叉查找树的删除

要删除的节点无子节点
要删除的节点只有左节点
- 该节点的parent指向待删节点的左节点，删除待删节点
要删除的节点只有右节点
- 该节点的parent指向待删节点的右节点，删除待删节点
要删除的节点有左右节点
- 在它的左子树中寻找最大的节点和它的parent，交换待删节点和这个最大节点，用parent删除该待删节点，并指向这个待删节点的左节点

非递归版：

cpp 复制代码

template<class K, class V>
struct BSTreeNode
{
	BSTreeNode(const K& key, const V& val) :_left(nullptr), _right(nullptr), _key(key), _val(val) {}

	BSTreeNode<K, V>* _left;
	BSTreeNode<K, V>* _right;
	K _key;
	V _val;
};
template<class K, class V>
class BSTree
{
	typedef BSTreeNode<K, V> Node;
public:
	void InOrder()
	{
		_InOrder(_root);
		cout << endl;
	}
	void _InOrder(Node* root)
	{
		if (root == nullptr) return;
		_InOrder(root->_left);
		cout << root->_key << " " << root->_val;
		_InOrder(root->_right);
	}
	Node* Insert(const K& key, const V& value)
	{
		if (_root == nullptr)
		{
			_root = new Node(key, value);
			return _root;
		}
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (key > cur->_key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (key < cur->_key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				return nullptr;
			}
		}
		cur = new Node(key, value);
		if (key > parent->_key) parent->_right = cur;
		else if (key < parent->_key)
		{
			parent->_left = cur;
		}
		return _root;
	}
public:
	Node* Find(const K& key)
	{
		Node* cur = _root;
		while (cur)
		{
			if (key > cur->_key) cur = cur->_right;
			else if (key < cur->_key) cur = cur->_left;
			else return cur;
		}
		return nullptr;
	}
	bool Erase(const K& key)
	{
		Node* parent = nullptr;
		Node* cur = _root;

		while (cur)
		{
			if (key > cur->_key) parent = cur,cur = cur->_right;
			else if (key < cur->key) parent = cur,cur = cur->_left;
			else
			{
				if (cur->_left == nullptr)
				{
					if (cur == _root) _root = cur->_right;
					else
					{
						if (parent->_right == cur) parent->_right = cur->_right;
						else parent->_left = cur->_right;
					}
				}
				else if (cur->_right = nullptr)
				{
					if (cur == _root) _root = cur->left;
					else
					{
						if (parent->_right == cur) parent->_right = cur->left;
						else parent->_left = cur->_left;
					}
				}
				else
				{
					Node* parent = cur;
					Node* leftMax = cur->_left;
					while (leftMax->_right)
					{
						parent = leftMax;
						leftMax = leftMax->_right;
					}
					swap(cur->_key, leftMax->_key);
					if (parent->_left == leftMax)
					{
						parent->_left = leftMax->_left;
					}
					else parent->_right = leftMax->_left;
					cur = leftMax;
				}
				delete cur;
				return true;
			}
		}
		return false;
	}
	
	
private:
	Node* _root = nullptr;
};

递归版：

解析ｉｎｓｅｒｔ

cpp 复制代码

bool InsertR(const K& key)
{
	return _InsertR(_root, key);
}

bool _InsertR(Node*& root ,const K& key)
{
	if (root == nullptr)
	{
		root = new Node(key);
		return true;
	}
	if (key > root->_key) return _InsertR(root->_right, key);
	else if (key < root->_key) return _InsertR(root->_left, key);
	else return false;
}

当传入根节点时，调用＿ＩｎｓｅｒｔＲ开始向下找值

Erase函数

cpp 复制代码

bool EraseR(const K& key)
{
	return _EraseR(_root, key);
}
bool _EraseR(Node*& root, const K& key)
{
	if (root == nullptr) return false;
	if (key > root->_key) return _EraseR(root->_right, key);
	else if (key < root->_key) return _EraseR(root->_left, key);
	else
	{
		Node* del = root;
		//左为空
		if (root->_left == nullptr) root = root->_right;
		//右为空
		else if (root->_right == nullptr) root = root->_left;
		//左右都不为空
		else
		{
			Node* leftMax = root;
			while (leftMax->_right)
			{
				leftMax = leftMax->_right;
			}
			swap(leftMax->_key, root->_key);
			return _EraseR(root->_left, key);
		}

		delete del; return true;
	}
}

ｄｅｓｔｏｒｙ

cpp 复制代码

void Destory(Node*& root)
{
	if (root == nullptr) return;

	Destory(root->_left);
	Destory(root->_right);
	delete root;
	root = nullptr;
}

Ｃｏｐｙ

cpp 复制代码

Node* Copy(Node* root)
{
	if (root == nullptr) return nullptr;

	Node* croot = new Node(root->_key);
	croot->_left = Copy(root->_left);
	croot->_right = Copy(root->_right);
	return croot;
}

二叉搜索树的应用

K（搜索）模型：

K模型即只有key作为关键词，结构中只需储存Key，关键码即为搜索的值
场景：快速判断在不在，门禁

KV（搜索）模型：

每一个关键码Key，与之对应的值Value，即＜Ｋｅｙ，Ｖａｌｕｅ＞的键值对
例如统计单词出现的个数，通过一个值找另外一个值，