Rust浮点数完全指南：从基础到实战避坑

Rust浮点数类型解析

Rust提供了两种原生浮点数类型，它们在内存占用和精度上有明显区别。f32是单精度浮点数，占用32位内存空间，而f64是双精度浮点数，占用64位。在现代CPU上，f64的运算速度几乎与f32相当，但精度更高，因此成为Rust的默认浮点类型。

rust 复制代码

fn main() {
    let x = 2.0; // 默认是 f64
    let y: f32 = 3.0; // 显式指定为 f32
    // 或者使用后缀写法
    let z = 3.14f32;
}

f32适用于一些对内存占用有严格要求的场景，如嵌入式系统或图形学中的顶点数据存储。而f64则更适合需要高精度计算的场景，如科学计算和金融应用。

严格的类型限制与转换

Rust以其内存安全著称，这种安全性也体现在浮点数的类型系统中。Rust不允许不同类型的数字直接运算，包括整数和浮点数之间，以及f32和f64之间的运算。

rust 复制代码

fn main() {
    let a = 10; // i32
    let b = 2.5; // f64
    // let c = a + b; // ❌ 报错：Rust 不会自动把整数变成浮点数
    // ✅ 正确做法：必须手动转换 (cast)
    let c = (a as f64) + b;
    println!("{}", c); // 输出 12.5
}

这种严格的类型限制虽然增加了一些代码量，但却避免了隐式转换可能带来的精度损失和难以追踪的bug，体现了Rust"安全优先"的设计哲学。

精度陷阱：为什么0.1 + 0.2不等于0.3

几乎所有编程语言都存在浮点数精度问题，Rust也不例外。这源于计算机采用IEEE 754标准来表示浮点数，而某些十进制小数无法精确转换为二进制表示。例如0.1的十进制小数转换为二进制是0.0001100110011...的无限循环，导致存储时产生截断误差。

rust 复制代码

fn main() {
    let a = 0.1;
    let b = 0.2;
    // ❌ 下面的判断会是 false
    // if a + b == 0.3 { ... }
    println!("0.1 + 0.2 = {:.20}", a + b); // 输出: 0.30000000000000004441
    // 显然它不完全等于 0.3
}

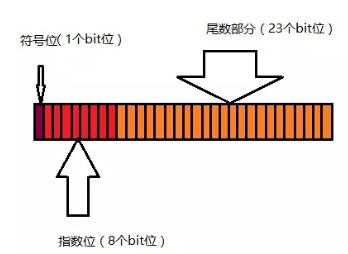
IEEE 754标准将浮点数分为符号位、指数位和尾数位。以32位浮点数为例，1位符号位，8位指数位，23位尾数位。这种结构导致某些十进制小数无法精确表示，就像我们无法用有限的十进制数字表示1/3一样。

正确比较浮点数的方法

既然直接比较浮点数不可靠，那么如何正确比较呢？答案是检查两个数的差值是否小于一个极小值，这个极小值被称为epsilon。

rust 复制代码

fn main() {
    let result = 0.1 + 0.2;
    let expected = 0.3;
    // f64::EPSILON 是一个极小的数 (大约 2.22e-16)
    if (result - expected).abs() < f64::EPSILON {
        println!("相等（在误差允许范围内）");
    }
}

Rust标准库为f32和f64都提供了EPSILON常量，分别表示各自类型能表示的最小正数。使用这种方法，我们可以在允许的误差范围内比较浮点数。

浮点数作为HashMap Key的限制

在Rust中，浮点数没有实现Eq特征，只实现了PartialEq特征。这是因为浮点数中存在NaN（Not a Number），而根据IEEE 754标准，NaN不等于任何值，包括它自己。

rust 复制代码

use std::collections::HashMap;

fn main() {
    let mut map = HashMap::new();
    // map.insert(2.0, "hello"); // ❌ 报错：f64 没有实现 Eq
    // 如果非要用浮点数做 Key，通常的做法是把它们转换成整数位表示，或者封装成自定义结构体手动实现 Eq。
}

如果确实需要将浮点数用作HashMap的Key，可以考虑以下几种方案：

将浮点数四舍五入到固定小数位数，然后转换为整数
ordered-float
将浮点数转换为其内存表示的整数形式

常用数学方法与特殊值处理

Rust的浮点数类型提供了丰富的数学方法，无需像C语言那样引入额外的数学库。

rust 复制代码

fn main() {
    let x: f64 = -42.5;
    println!("{}", x.abs()); // 绝对值: 42.5
    println!("{}", x.floor()); // 向下取整: -43.0
    println!("{}", x.ceil()); // 向上取整: -42.0
    println!("{}", x.round()); // 四舍五入: -43.0

    let angle = std::f64::consts::PI;
    println!("{}", angle.sin()); // 正弦值
    println!("{}", 4.0_f64.sqrt()); // 开方: 2.0
}

Rust还支持处理特殊的浮点值，如无穷大和NaN：

rust 复制代码

fn main() {
    let x = 1.0 / 0.0;
    println!("{}", x); // 输出 "inf"
    println!("{}", x.is_infinite()); // true

    let y = 0.0 / 0.0;
    println!("{}", y); // 输出 "NaN"
    println!("{}", y.is_nan()); // true
}

在处理浮点数时，特别是从外部输入或进行除法运算时，一定要注意检查这些特殊值，以避免程序异常。

总结：Rust浮点数的设计哲学

Rust对浮点数的处理体现了其整体设计哲学：安全、明确和高性能。通过严格的类型检查，Rust避免了隐式转换可能带来的错误；通过不实现Eq特征，Rust提醒开发者浮点数比较的潜在问题；同时，Rust提供了丰富的数学方法和特殊值处理，确保了浮点数运算的灵活性和安全性。

对于Rust初学者来说，理解浮点数的这些特性可能需要一些时间，但掌握这些知识将帮助你编写更安全、更可靠的代码。记住，在处理浮点数时，始终要考虑精度问题，并使用适当的比较方法。

希望这篇指南能帮助你更好地理解和使用Rust中的浮点数。如果你有任何问题或建议，欢迎在评论区留言讨论！