[C++进阶]深入理解二叉搜索树

小明同学012026-01-25 12:03

目录

一、二叉搜索树简介

[BST 定义与核心特性](#BST 定义与核心特性)

节点结构体定义

BST的核心操作

二、BST核心功能实现

1、插入的实现

2、查找的实现

3、中序遍历

三、核心功能删除（重点）

四、递归实现

1、代码实现

2、运行结果

3、核心重点

[4、BST 的缺陷与优化](#4、BST 的缺陷与优化)

一、二叉搜索树简介

二叉搜索树即 Binary Search Tree（左右不要写反喔），是数据结构中最基础也最实用的树形结构之一，它以 "左子树值小于根、右子树值大于根" 的核心特性，实现了高效的增删查操作。是哈希表、红黑树等高级数据结构的基础，本文将全面讲解 BST 的核心功能、实现细节。

BST 定义与核心特性

二叉搜索树是一种满足以下性质的二叉树：

  • 任意节点的左子树中，所有节点的键值（Key）均小于该节点的键值；
  • 任意节点的右子树中，所有节点的键值均大于该节点的键值；
  • 左、右子树本身也必须是二叉搜索树（递归定义）；

节点结构体定义

cpp 复制代码 
template<class K>
struct BSTreeNode
{
    BSTreeNode<K>* _left;   
    BSTreeNode<K>* _right;  
    K _key;                 


    BSTreeNode(const K& key)
        :_left(nullptr)    
        ,_right(nullptr)
        ,_key(key)
    {}
};
  • 模板参数K：类模板，让节点支持任意可比较的类型
  • 结构体成员：_left/_right指向子节点，_key为核心键值
  • 构造函数：使用const K&传参，既避免拷贝，又保证不修改传入的键值

BST的核心操作

cpp 复制代码 
template<class K>
class BSTree
{
    typedef BSTreeNode<K> Node;
public:
    BSTree()
        :_root(nullptr)
    {}

    bool Insert(const K& key);
    bool Find(const K& key);
    bool Erase(const K& key);
    void InOrder();

private:
    void _InOrder(Node* root);
    Node* _root; 
};

讲解

  • typedef BSTreeNode<K> Node：类型别名，简化代码书写，省事儿
  • 根节点_root私有化：防止外部直接修改根节点，只能通过类的成员函数操作
  • void _InOrder(Node* root)私有，防止外部传入错误根节点

二、BST核心功能实现

1、插入的实现

插入是 BST 最基础的操作，核心逻辑是先找到空位置，按大小关系挂个新节点，不允许重复键值。

cpp 复制代码 
bool BSTree<K>::Insert(const K& key)
{
    if (_root == nullptr)
    {
        _root = new Node(key);  
        return true;          
    }

    // 情况2：非空树 → 遍历找插入位置
    Node* parent = nullptr;  
    Node* cur = _root;       
    while (cur)  
    {
        if (cur->_key < key)  
        {
            parent = cur;
            cur = cur->_right;
        }
        else if (cur->_key > key) 
        {
            parent = cur;
            cur = cur->_left;
        }
        else  
        {
            return false;
        }
    }


    cur = new Node(key);
    if (parent->_key < key)
    {
        parent->_right = cur;  
    }
    else
    {
        parent->_left = cur;   
    }

    return true;  
}

这是迭代版本的插入的实现，最关键的一点就是保留父子关系，不断更改parent的位置，进而迭代遍历

  • 空树处理：空树则直接创建根节点
  • 遍历找位置 ：
    • parent记录父节点，cur负责遍历，两者配合找到空位置后挂新节点
    • 利用 BST "左小右大" 的特性，不断缩小查找范围，直到cur为空
  • 挂新节点 ：根据parent->_key和新key的大小关系，决定挂左还是挂右
  • BST 的键值必须唯一，遇到重复直接返回false。
  • 迭代插入的优势：无函数调用开销，性能虽然略高递归版，但是无栈溢出风险，递归深度太高了会溢出。

2、查找的实现

查找是 BST 的核心优势，利用 "左小右大" 的特性，可以快速缩小查找范围

cpp 复制代码 
bool BSTree<K>::Find(const K& key)
{
    Node* cur = _root; 
    while (cur)
    {
        if (cur->_key < key)  
        {
            cur = cur->_right;
        }
        else if (cur->_key > key)  
        {
            cur = cur->_left;
        }
        else  
        {
            return true;
        }
    }
    return false; 
}

比较简单，用cur遍历树，key大的话就去右子树继续找，小的话就去左子树找。

时间复杂度：理想状态O(logn)，最坏状态O(n)，显而易见嘛，BST 的查找效率远高于数组，这是树形结构的核心优势

3、中序遍历

cpp 复制代码 
void BSTree<K>::InOrder()
{
    _InOrder(_root);
    cout << endl;  
}

void BSTree<K>::_InOrder(Node* root)
{
    if (root == nullptr)  
    {
        return;
    }

    _InOrder(root->_left);        
    cout << root->_key << " ";    
    _InOrder(root->_right);      
}

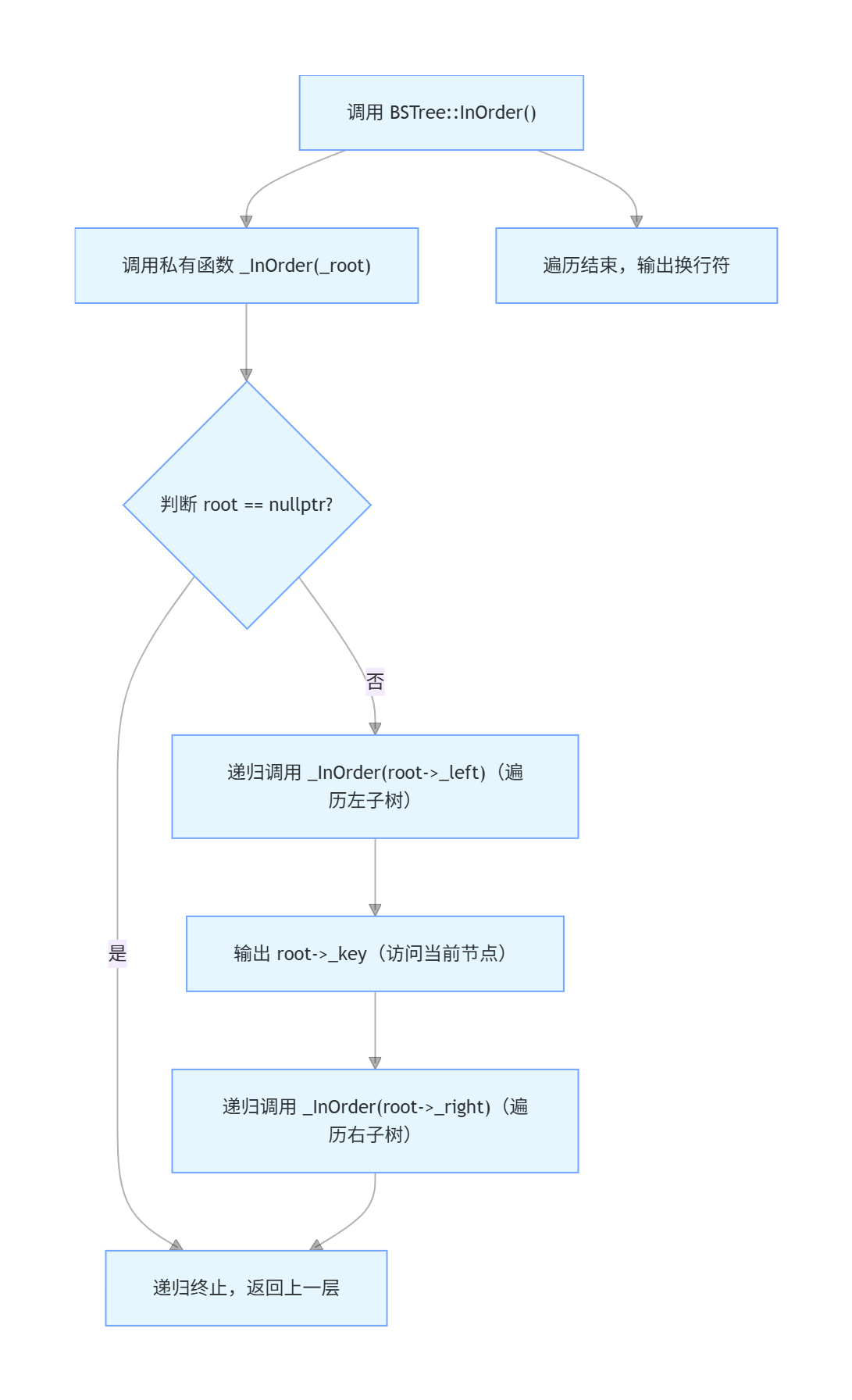
这是递归的流程图

  • 中序遍历顺序：左 、根、 右，这是 BST 升序的核心原因
  • 递归终止，root == nullptr（空树 / 叶子节点的孩子）
  • 对外提供InOrder()接口，隐藏递归函数_InOrder()

三、核心功能删除（重点）

删除是 BST 最复杂的操作，核心原则是 "删除节点后，仍保持 BST 的性质"。这是最阴的，需分三种情况处理

cpp 复制代码 
bool BSTree<K>::Erase(const K& key)
{
    Node* parent = nullptr;
    Node* cur = _root;

    while (cur)
    {
        if (cur->_key < key)
        {
            parent = cur;
            cur = cur->_right;
        }
        else if (cur->_key > key)
        {
            parent = cur;
            cur = cur->_left;
        }
        else  
        {
           
            if (cur->_left == nullptr)
            {
                if (cur == _root)
                {
                    _root = cur->_right;
                }
                else  
                {
                    if (parent->_right == cur)
                    {
                        parent->_right = cur->_right;
                    }
                    else
                    {
                        parent->_left = cur->_right;
                    }
                }
            }
            else if (cur->_right == nullptr)
            {
                if (cur == _root)
                {
                    _root = cur->_left;
                }
                else
                {
                    if (parent->_right == cur)
                    {
                        parent->_right = cur->_left;
                    }
                    else
                    {
                        parent->_left = cur->_left;
                    }
                }
            }
            else
            {

                Node* replaceParent = cur;  // 重置parent，专门找替代节点
                Node* leftMax = cur->_left;
                while (leftMax->_right)
                {
                    replaceParent = leftMax;
                    leftMax = leftMax->_right;
                }

                // 交换cur和leftMax的key
                swap(cur->_key, leftMax->_key);

                if (replaceParent->_left == leftMax)
                {
                    replaceParent->_left = leftMax->_left;
                }
                else
                {
                    replaceParent->_right = leftMax->_left;
                }

                cur = leftMax;  
            }

            delete cur; 
            return true;
        }
    }

    return false; 
}

这里提供了迭代版的删除实现

情况 1（左空）或 情况 2（右空）

  • 直接让父节点跳过当前节点，指向当前节点的非空孩子
  • 特殊处理根节点：若删除的是根节点，需将_root指向非空孩子
  • 情况 3（左右都非空）：
  • 不能直接删，直接删除会导致 cur 的左右子树 "失联"，破坏 BST 结构
  • 替代方案：找 "左子树的最大值" 或 "右子树的最小值"（这两个节点必为叶子 / 单孩子节点，符合情况 1/2）
  • 操作逻辑：交换 cur 和替代节点的 key → 删除替代节点（此时替代节点是易删除的情况）
  • 删除节点后必须调用delete cur，否则会导致内存泄漏

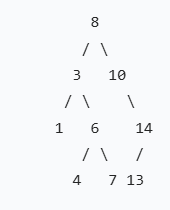
我们用这棵树举例子

待删节点左孩子为空（例：删除 10）

找到待删节点cur=10，parent=8

判断cur左孩子为空 → 检查cur不是根节点

parent(8)的右孩子是cur(10) → 把parent->_right指向cur->_right(14)
待删节点左右孩子都存在（例：删除 3）

找到待删节点cur=3，parent=8（cur左右孩子都存在，左=1，右=6）

步骤2：找cur左子树的最右节点： replaceParent初始=3，leftMax初始=1 → leftMax->_right=nullptr，所以替代节点是1

步骤3：交换cur(3)和leftMax(1)的key → cur->_key=1，leftMax->_key=3

步骤4：删除替代节点leftMax(1)： replaceParent(3)的左孩子是leftMax(1) → 把replaceParent->_left置为leftMax->_left(nullptr)

步骤5：删除leftMax(1)

四、递归实现

迭代版本非常的冗长，考试时可以使用递归版本进行解决

1、代码实现

cpp 复制代码 
#pragma once
#include <iostream>
#include <string>
using namespace std;

namespace BSTree_Enhanced
{
    template<class K>
    struct BSTreeNode
    {
        BSTreeNode<K>* _left;
        BSTreeNode<K>* _right;
        K _key;

        BSTreeNode(const K& key)
            :_left(nullptr)
            ,_right(nullptr)
            ,_key(key)
        {}
    };

    template<class K>
    class BSTree
    {
        typedef BSTreeNode<K> Node;
    public:
        BSTree() :_root(nullptr) {}

        // 深拷贝（避免浅拷贝问题）
        BSTree(const BSTree<K>& t)
        {
            _root = Copy(t._root);
        }

        // 赋值运算符重载
        BSTree<K>& operator=(BSTree<K> t)
        {
            swap(_root, t._root);
            return *this;
        }

        ~BSTree()
        {
            Destroy(_root);
        }

        bool InsertR(const K& key) { return _InsertR(_root, key); }
        bool FindR(const K& key) { return _FindR(_root, key); }
        bool EraseR(const K& key) { return _EraseR(_root, key); }

        void InOrder()
        {
            _InOrder(_root);
            cout << endl;
        }

    private:
        Node* Copy(Node* root)
        {
            if (root == nullptr) return nullptr;

            Node* newNode = new Node(root->_key);
            newNode->_left = Copy(root->_left);
            newNode->_right = Copy(root->_right);
            return newNode;
        }

        // （后序遍历：左→右→根）
        void Destroy(Node*& root)  
        {
            if (root == nullptr) return;

            Destroy(root->_left);   
            Destroy(root->_right);  
            delete root;           
            root = nullptr;         
        }

        bool _InsertR(Node*& root, const K& key)
        {
            if (root == nullptr)
            {
                root = new Node(key);  // 引用传参，直接修改原指针
                return true;
            }

            if (root->_key < key)
            {
                return _InsertR(root->_right, key);
            }
            else if (root->_key > key)
            {
                return _InsertR(root->_left, key);
            }
            else
            {
                return false;  // 重复key
            }
        }

        bool _FindR(Node* root, const K& key)
        {
            if (root == nullptr) return false;

            if (root->_key < key) return _FindR(root->_right, key);
            else if (root->_key > key) return _FindR(root->_left, key);
            else return true;
        }

        // 递归删除核心（最关键）
        bool _EraseR(Node*& root, const K& key)
        {
            if (root == nullptr) return false;

            if (root->_key < key) return _EraseR(root->_right, key);
            else if (root->_key > key) return _EraseR(root->_left, key);
            else  
            {
                Node* del = root;

                // 左空 → 指向右孩子
                if (root->_left == nullptr)
                {
                    root = root->_right;
                }
                // 右空 → 指向左孩子
                else if (root->_right == nullptr)
                {
                    root = root->_left;
                }
                else
                {
                    Node* leftMax = root->_left;
                    while (leftMax->_right) leftMax = leftMax->_right;

                    swap(root->_key, leftMax->_key);
                    return _EraseR(root->_left, key);  
                }

                delete del;
                return true;
            }
        }

        // 中序遍历递归实现
        void _InOrder(Node* root)
        {
            if (root == nullptr) return;
            _InOrder(root->_left);
            cout << root->_key << " ";
            _InOrder(root->_right);
        }

    private:
        Node* _root;
    };

    void TestBSTree_Enhanced1()
    {
        int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };
        BSTree<int> t;
        for (auto e : a) t.InsertR(e);
        cout << "递归插入后中序遍历：";
        t.InOrder();  

        BSTree<int> t1(t);
        cout << "拷贝构造后t1中序遍历：";
        t1.InOrder();  // 与t一致

        t.EraseR(3);
        cout << "递归删除3后中序遍历：";
        t.InOrder();  
    }
}

2、运行结果

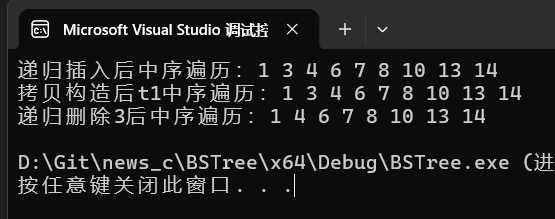
3、核心重点

1、深拷贝（Copy）：

  • 浅拷贝问题：直接赋值_root = t._root会导致两个对象共用同一棵树，析构时重复释放内存（程序崩溃）

  • 深拷贝逻辑：递归创建新节点，复制每一个节点的 key，形成独立的树

  • 前序遍历保证 、先有根，再挂孩子
    递归插入 / 删除：

  • 引用传参是核心：无需记录父节点，直接修改原指针（如root = root->_right），等价于迭代版中 "父节点指向孩子" 的操作；

  • 递归删除更简洁：找替代节点后，递归删除左子树的最大值，将复杂问题分解为子问题。

4、BST 的缺陷与优化

基础 BST 的最大问题是 易退化，比如插入有序序列会退化为链表，导致效率下降

  1. AVL 树：严格平衡二叉树，任意节点的左右子树高度差≤1，通过旋转（左旋、右旋、左右旋、右左旋）保持平衡
  2. 红黑树：近似平衡二叉树，通过 "红黑规则"（节点红 / 黑、根黑、红节点子节点黑等）保持平衡，旋转和变色操作更少，性能优于 AVL 树
  3. 后续博客我们继续研究

以上就是本篇博客的全部内容了，欢迎大家在评论区交流讨论

相关推荐
muddjsv1 小时前
Git Amend 完全解析：修改最近提交的正确姿势与避坑指南
git
点云SLAM2 小时前
C++std::enable_if_t 与 std::is_same_v使用
c++·模板元编程·c++ 类型萃取·enable_if_t·is_same_v
C+++Python2 小时前
C++ vector
开发语言·c++·算法
莫问前路漫漫2 小时前
Python包管理工具pip完整安装教程
开发语言·python
superman超哥2 小时前
处理复杂数据结构：Serde 在实战中的深度应用
开发语言·rust·开发工具·编程语言·rust serde·rust数据结构
Java程序员威哥2 小时前
Arthas+IDEA实战：Java线上问题排查完整流程（Spring Boot项目落地）
java·开发语言·spring boot·python·c#·intellij-idea
superman超哥2 小时前
错误处理与验证：Serde 中的类型安全与数据完整性
开发语言·rust·编程语言·rust编程·rust错误处理与验证·rust serde
ssxueyi2 小时前
Git 完整安装与环境配置教程（Windows/macOS/Linux 通用）
windows·git·macos·项目管理·git教程·代码管理
夔曦2 小时前
【python】月报考勤工时计算
开发语言·python
热门推荐
01GitHub 镜像站点02OpenCode 入门教程：介绍 · 安装 · 配置第三方 API (如 Claude)03Claude Code Skills 实用使用手册04Linux下V2Ray安装配置指南05UV安装并设置国内源06Open Code教程（四）| 高级配置与集成07BongoCat - 跨平台键盘猫动画工具08在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）09安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）10MC.JS 网页版《我的世界》 免安装中文版