学习视频来源:https://www.bilibili.com/video/BV1Vt411X7JF/?p=16
本博客除了包含自己的在学习过程中记录的笔记外,还包含少部分自己扩展的内容,如有错误,敬请指正。
文章目录
- [问题: 如何维护以太坊账户状态](#问题: 如何维护以太坊账户状态)
- [1. 第一种方案:初始想法:哈希表?](#1. 第一种方案:初始想法:哈希表?)
-
- [1.1 特点](#1.1 特点)
- [1.2 尝试:把所有哈希表元素放进默克尔树](#1.2 尝试:把所有哈希表元素放进默克尔树)
- [2. 第二种方案:直接用默克尔树?](#2. 第二种方案:直接用默克尔树?)
- [3. 解决方案------MPT(状态树)](#3. 解决方案——MPT(状态树))
-
- [3.1 Trie(前缀树)](#3.1 Trie(前缀树))
-
- 特性
- [为什么 Trie 比哈希表好?](#为什么 Trie 比哈希表好?)
- [Trie 的缺点与优化](#Trie 的缺点与优化)
- [3.2 Patricia Trie(压缩前缀树)](#3.2 Patricia Trie(压缩前缀树))
- [3.3 Merkle Patricia Trie(MPT)](#3.3 Merkle Patricia Trie(MPT))
- [4. RLP 序列化](#4. RLP 序列化)
- [5. 总结](#5. 总结)
问题: 如何维护以太坊账户状态
在以太坊中,我们要做的事情,就是维护一个 地址到状态的映射 :addr → state。
- 地址是一个 160 位(bits)的数 ,通常用 40 个十六进制字符表示(因为 160 ÷ 4 = 40)。
- 外部账户的状态包括:余额(balance) 和 交易次数(nonce)。
- 合约账户的状态还包括:代码(code) 和 存储(storage)。
1. 第一种方案:初始想法:哈希表?
1.1 特点
一个直观的想法是用 哈希表 实现这个映射:key 是地址,value 是状态。
哈希表查询效率很高,但它解决不了关键问题:无法提供默克尔证明(Merkle Proof)。
比如,你和别人签合同,希望他证明自己有多少钱------仅靠哈希表做不到。
1.2 尝试:把所有哈希表元素放进默克尔树
一种方法是把哈希表中所有元素组织成一棵 默克尔树 ,将根哈希值写入区块头并公布。
轻节点验证时,向全节点请求 默克尔路径 + 账户余额,自行计算是否匹配。
但问题来了:
- 每发布一个新区块,部分账户状态会变;
- 如果每次都重建树,代价太大(尽管只有少量账户变化)。
对比比特币:它只对当前区块内的交易 建默克尔树,交易数有限(一般 ≤4000),且树一旦发布就不再修改。
但以太坊要维护全局账户状态,不能照搬此法,因为账户数多。
2. 第二种方案:直接用默克尔树?
放弃哈希表,直接用一棵大默克尔树存所有账户。
但又出现新问题:
- 默克尔树本身不支持高效查询/更新;
- 如果账户叶节点不排序 ,不同节点收到交易顺序不同,构建出的树结构不同,根哈希就不一致,无法保证一致性。
比特币也存在类似问题,但它通过"由出块者决定交易顺序"来解决------谁获得记账权,谁说了算。其他人只需接受最终区块中的默克尔树。
如果以太坊这么做:
- 需要把整棵状态树放进区块,但树太大,不可行;
- 若强制排序 ,虽能保证一致性,但每新增一个地址都要重建树,可能半个树都需要重建,开销依然巨大。
3. 解决方案------MPT(状态树)
3.1 Trie(前缀树)
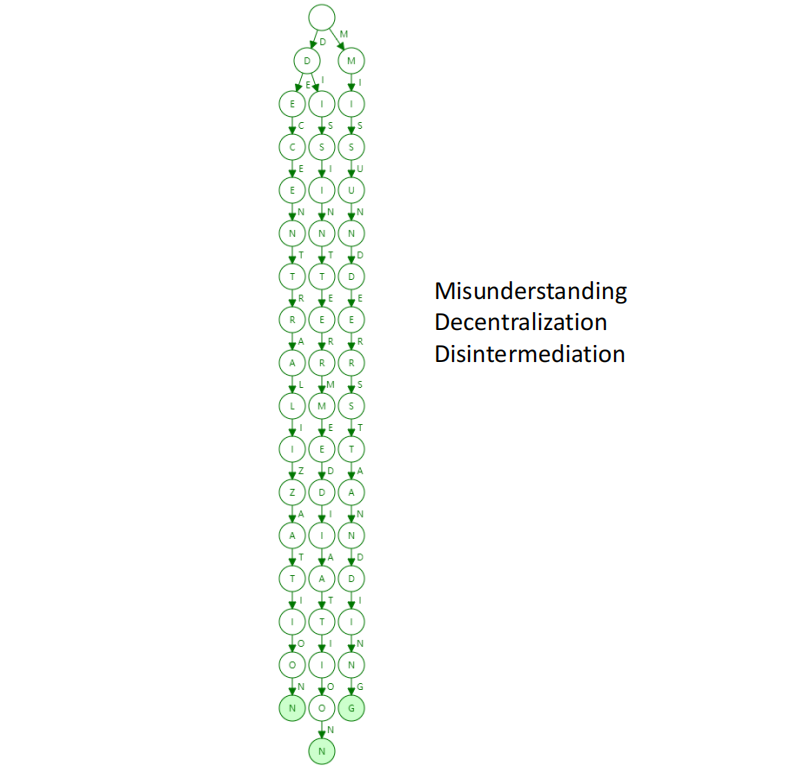
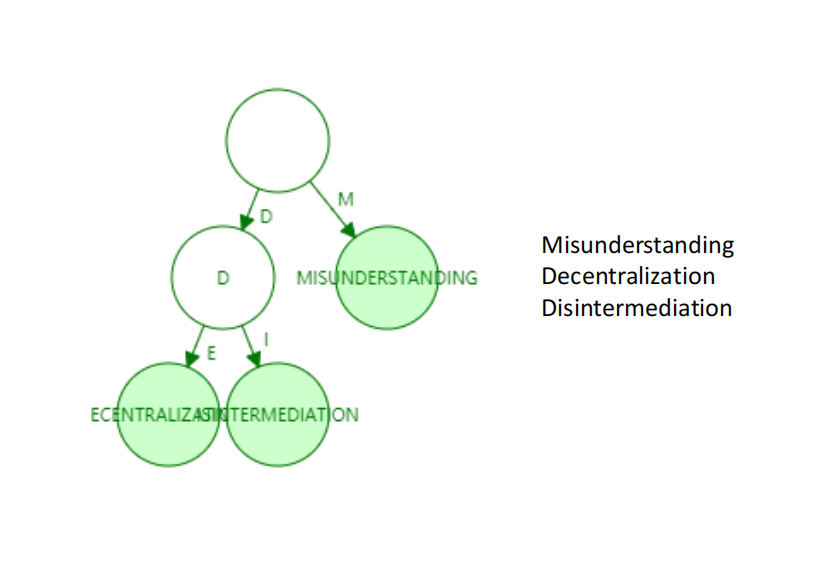
于是,以太坊选择了 Trie(发音同 "try") ,全称来自 retrieval (检索),也叫前缀树 。大家应都熟悉,就不讲了。结构如下:
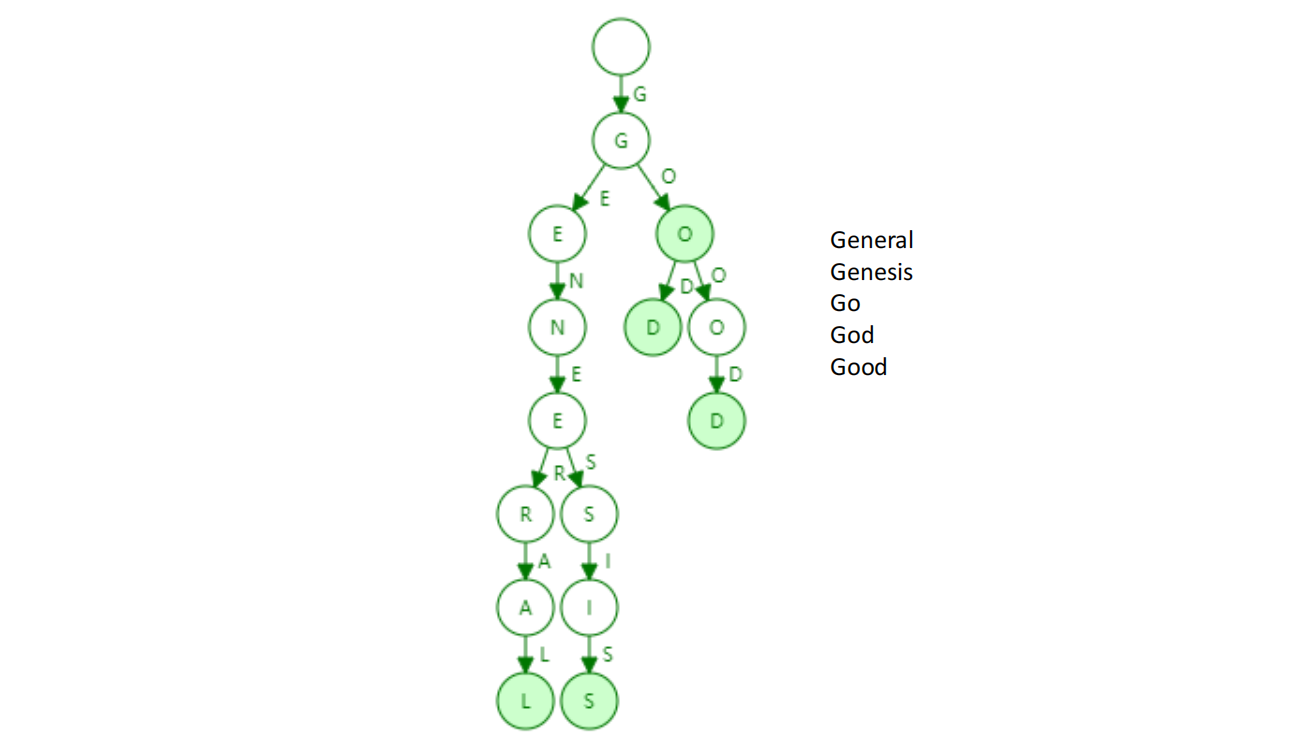
特性
- 以太坊地址字符取值是(0-f)分叉的 branching factor 是 0--f(即 16 叉),对应十六进制每一位;
- 每个路径末尾加一个结束标志位,表示这是一个完整 key(如地址);
- 比特币和以太坊的地址不通用 ,长度也不同,但都是从公钥哈希后截取后 160 位得到。
比特币 vs 以太坊 地址机制详细对比表
| 对比项 | 比特币(Bitcoin) | 以太坊(Ethereum) |
|---|---|---|
| 最终地址长度(比特) | 160 位(20 字节) | 160 位(20 字节) |
| 用户可见地址格式 | - Legacy: Base58Check(如 1A1z...)- SegWit: Bech32(如 bc1q...) |
40 位十六进制字符串,通常带 0x 前缀(如 0x742d...),支持 EIP-55 校验和(通过大小写编码) |
| 公钥 → 地址的核心哈希算法 | RIPEMD-160(SHA-256(公钥)) | Keccak-256(公钥) |
| 是否截取哈希的一部分? | ❌ 否RIPEMD-160 直接输出 160 位 | ✅ 是Keccak-256 输出 256 位,取后 20 字节(即后 160 位) |
| 椭圆曲线(私钥 → 公钥) | secp256k1公钥 = 私钥 × 基点 G | **secp256k1(完全相同)**✅ 同一私钥在 BTC 和 ETH 上生成完全相同的公钥(字节序列一致) |
| 典型地址示例 | 1A1zP1eP5QGefi2DMPTfTL5SLmv7DivfNa,bc1qar0srrr7xfkvy5l643lydnw9re59gtzzwf5mdq |
0x742d35Cc6634C0532925a3b8D4C9Fb2f2F2F2F2F |
为什么 Trie 比哈希表好?
-
无碰撞 :
哈希表可能因哈希冲突需要处理碰撞;而 Trie 中,只要输入(地址)不同,路径必然不同,天然避免冲突。
-
结构确定性 :
前面讲的普通默克尔树,若叶节点顺序不同,整棵树就不同;
但 Trie 只要输入集合相同,无论插入顺序如何,最终树结构完全一致 。
→ 不同全节点构建出的状态树根哈希一定相同。
-
局部更新高效 :
修改一个账户状态时,只需更新从根到该叶节点的路径,其余部分共享,无需重建整棵树。
Trie 的缺点与优化
- 存储浪费 :
当树很稀疏时(比如只有一个子节点一路向下),普通 Trie 会退化成一条链,大量中间节点只含一个指针,浪费空间。
3.2 Patricia Trie(压缩前缀树)
压缩前缀树即对连续单子节点路径("一脉单传")进行路径压缩。
特性
- 压缩后,树高度大幅缩短,访问内存次数减少;
- 但如果后续插入的新 key 在压缩路径上产生分叉 ,就需要将压缩节点重新展开。
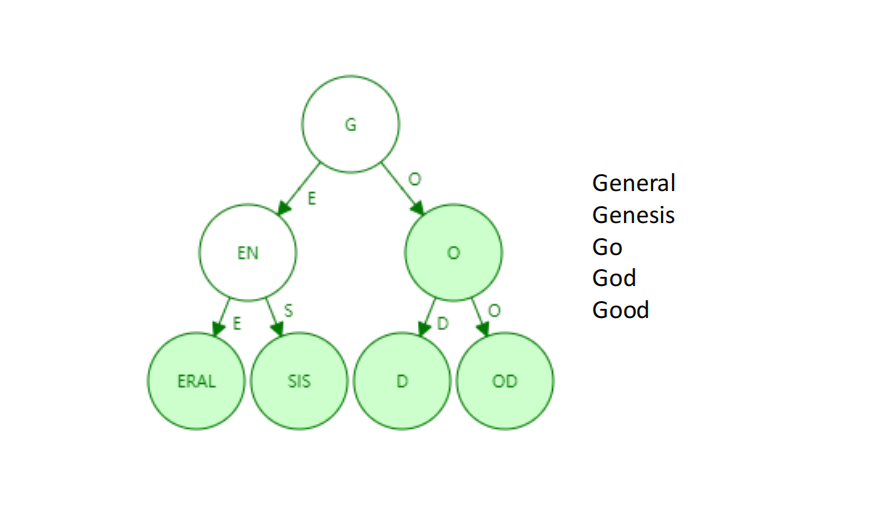
什么情况适合压缩?------树非常稀疏时
以太坊地址空间是 2¹⁶⁰ ,极其庞大; 但实际使用的账户数量远远小于这个值,所以树非常稀疏。
那么为什么地址空间要这么大呢?------防止碰撞。若强行缩小地址空间(如用更短哈希),理论上可能碰撞。
但按现有地址生成方式(Keccak-256 截取),碰撞概率比地球爆炸还低 ,可忽略不计。
压缩前
压缩后
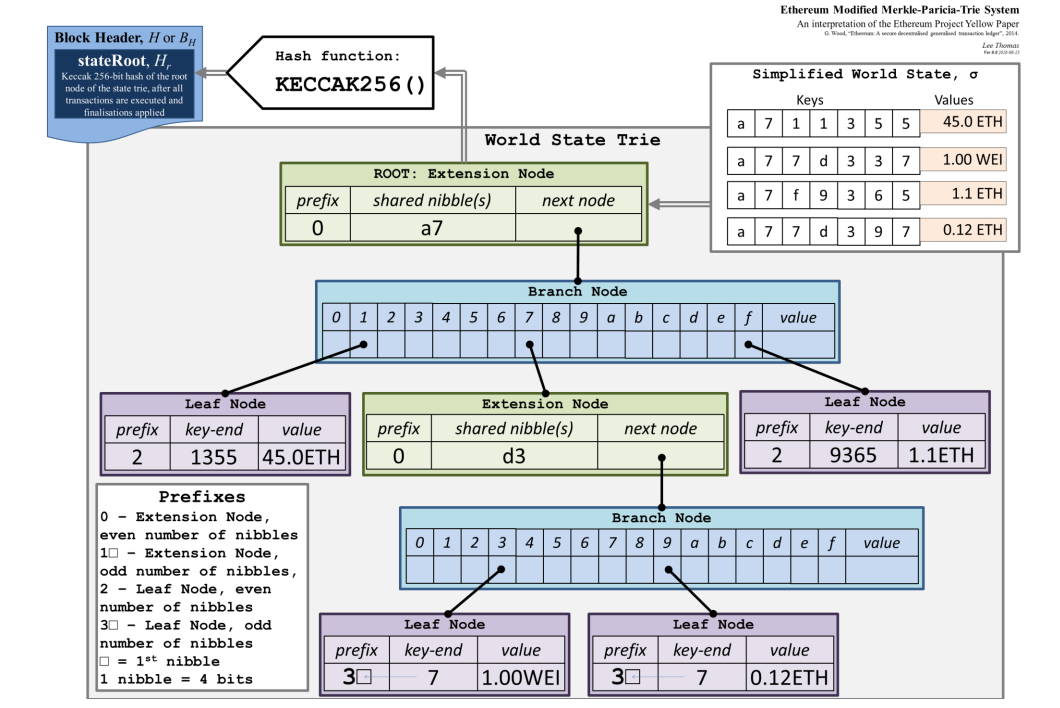
3.3 Merkle Patricia Trie(MPT)
以太坊进一步将 Patricia Trie 改造成 Merkle Patricia Trie(MPT) ,也叫状态树 。以太坊使用的是 Modified MPT,有一些工程优化,但核心思想不变
特性
- 将普通指针替换为 哈希指针(即子节点的哈希值);
- 这样整棵树可递归计算出一个 根哈希(state root),写入区块头;
- 实现 防篡改 + 默克尔证明:轻节点可通过路径验证某账户余额;
- 甚至能证明某个账户不存在:提供该地址应处位置的默克尔路径,若该位置为空,则证明其不存在。
- 且查找和更新效率高!
状态快照------用于回滚
- 每次新区块产生,系统生成新的 MPT;
- 未变化的节点被多个版本共享,节省存储;
- 保留历史状态 是为了应对临时分叉:失败链需回滚到分叉点,再重放成功链交易。 这与比特币不同:比特币交易是"消耗型"的,状态可推导;但以太坊有智能合约,执行后状态复杂,无法逆向还原,必须显式保存历史。
PS:回滚不用从最后一个区块,挨个回滚到分叉点,而是直接从分叉点区块,根据区块头stateRoot,加载当时的历史状态,再应用重放成功链交易
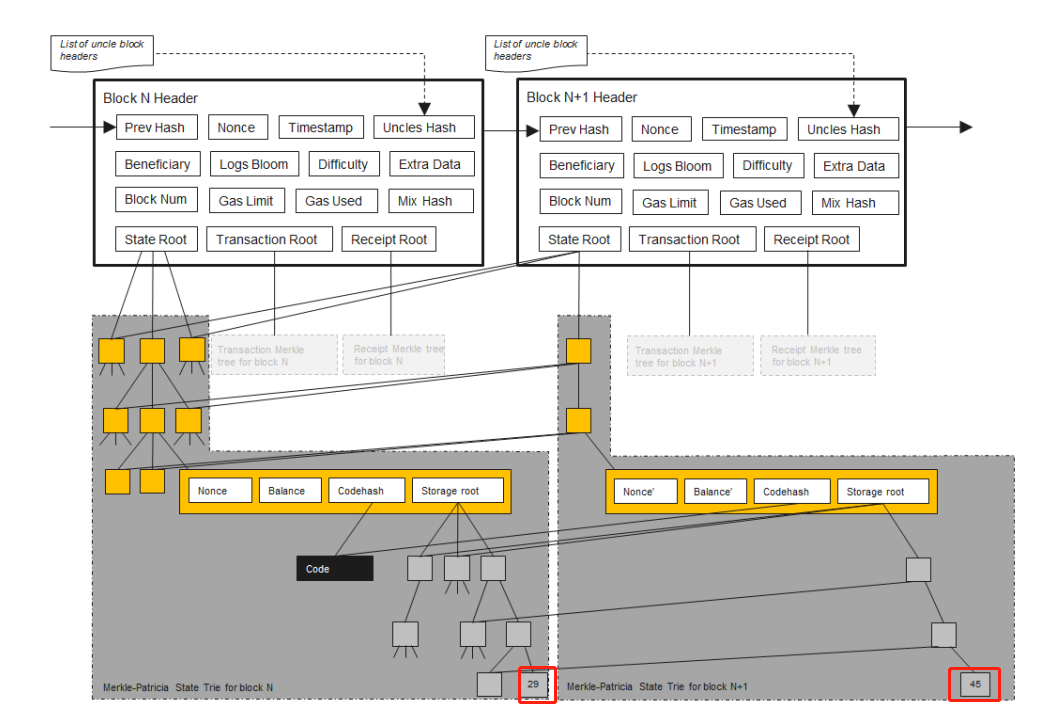
上图中,是一个合约账户存储中的某个值发生了变化。发生变化的节点相关路径变化上的节点新建,其他的节点共享。合约账户存储也是一个小的MPT,路径是slot号编码,值就是存储的值。
4. RLP 序列化
MPT 中的 value(账户状态)需先经 RLP(Recursive Length Prefix) 序列化再存储。
- RLP 是一种极简的序列化格式:
- 只支持两种类型:字节数组(bytes) 和 嵌套列表(list of items);
- 所有数据(整数、哈希、结构体等)最终都转为字节数组;
- 相比 Protocol Buffers 等复杂格式,RLP 不做类型检查、不压缩、不加密 ,
把复杂性留给应用层,实现简单、确定性强。
5. 总结
以太坊没有用哈希表,也没有用普通默克尔树,而是选择了 Merkle Patricia Trie 来维护全局状态:
- 利用 Trie 的结构特点保证高效查询和更新;
- 利用 Trie 的确定性结构保证节点间一致性;
- 通过路径压缩优化稀疏树的空间效率;
- 借助哈希指针实现默克尔证明与防篡改;
- 配合 RLP 序列化 和状态快照机制,支撑智能合约的复杂状态演化。
这一设计,是以太坊实现"世界计算机"愿景的基石之一。