【通信原理】信道——信道、传输特性、多径效应、噪声、带宽、信道容量（笔记总结）

通信原理第三章：信道学习笔记

文章目录

通信原理第三章：信道学习笔记
- [1. 信道定义与数学模型](#1. 信道定义与数学模型)
- - [1.1 信道的定义及分类](#1.1 信道的定义及分类)
  - - 狭义信道与广义信道
    - 恒参信道与随参信道
  - [1.2 调制信道数学模型](#1.2 调制信道数学模型)
  - [1.3 编码信道数学模型](#1.3 编码信道数学模型)
- [2. 恒参信道的传输特性](#2. 恒参信道的传输特性)
- - [2.1 理想恒参信道特性](#2.1 理想恒参信道特性)
  - [2.2 实际恒参信道特性](#2.2 实际恒参信道特性)
- [3. 随参信道的传输特性](#3. 随参信道的传输特性)
- - [3.1 随参信道的特点](#3.1 随参信道的特点)
  - [3.2 多径传播的影响](#3.2 多径传播的影响)
- [4. 噪声与带宽](#4. 噪声与带宽)
- - [4.1 信道噪声](#4.1 信道噪声)
  - [4.2 等效噪声带宽](#4.2 等效噪声带宽)
  - [4.3 各类带宽概念](#4.3 各类带宽概念)
- [5. 信道容量](#5. 信道容量)
- - [5.1 离散信道的信道容量](#5.1 离散信道的信道容量)
  - [5.2 连续信道的信道容量](#5.2 连续信道的信道容量)

1. 信道定义与数学模型

1.1 信道的定义及分类

信道是通信系统中连接发送端和接收端的物理媒介或逻辑通路，用于传输信号。

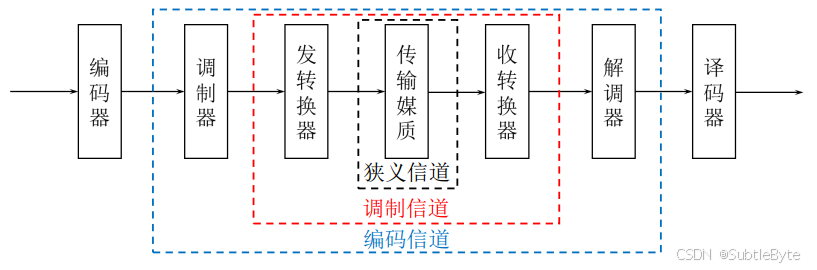
狭义信道与广义信道

狭义信道 ：仅指传输媒质，如电缆、光纤、大气等物理媒介。
广义信道 ：在传输媒质的基础上，还包括相关的信号转换设备。根据研究问题的不同，广义信道可分为：
- 调制信道：从调制器输出端到解调器输入端，用于研究调制/解调问题。
- 编码信道：从编码器输出端到译码器输入端，用于研究编码/译码问题。

恒参信道与随参信道

恒参信道 ：信道传输特性随时间变化极其缓慢 或基本不变 。例如：
- 有线信道：同轴电缆、对称电缆（双绞线）、光纤。
- 无线信道：卫星中继信道、超短波/微波视距传播信道。
随参信道 ：信道传输特性随时间随机快速变化 。例如：
- 无线信道：短波电离层反射信道、对流层散射信道、移动通信信道。

1.2 调制信道数学模型

调制信道是对信号进行变换（调制后）传输的信道，其特点如下：

有一对或多对输入端和输出端。
通常满足线性叠加原理（线性网络）。
对信号有固定或时变的延迟和损耗。
即使没有信号输入，也可能有噪声输出。

其数学模型可以抽象为一个 叠加有噪声的线性时变/时不变滤波器。

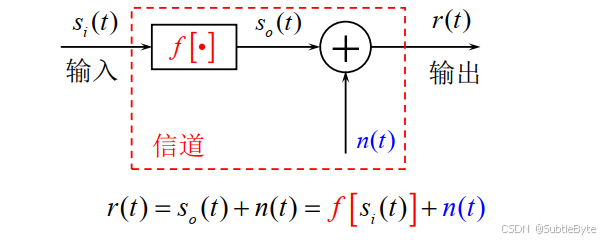
r ( t ) = s o ( t ) + n ( t ) = f [ s i ( t ) ] + n ( t ) r(t) = s_o(t) + n(t) = f[s_i(t)] + n(t) r(t)=so(t)+n(t)=f[si(t)]+n(t)

r ( t ) r(t) r(t)：信道输出信号（接收信号）。
s i ( t ) s_i(t) si(t)：信道输入信号（已调信号）。
f [ ⋅ ] f[\cdot] f[⋅]：信道对输入信号的变换作用，即乘性干扰。

因为它与信号是相乘的关系，所以当没有输入信号时，信道输出端也没有乘性干扰输出。
n ( t ) n(t) n(t)：信道引入的加性噪声。

当没有信号输入时，信道输出端也有加性干扰输出

对于不同类型的信道， f [ ⋅ ] f[\cdot] f[⋅] 的具体形式不同：

恒参信道 ： f [ ⋅ ] f[\cdot] f[⋅] 是一个线性时不变滤波器，其冲激响应为 c ( t ) c(t) c(t)，频率响应为 C ( ω ) C(\omega) C(ω)。输出信号 s o ( t ) = s i ( t ) ∗ c ( t ) s_o(t) = s_i(t) * c(t) so(t)=si(t)∗c(t)，或 S o ( ω ) = S i ( ω ) ⋅ C ( ω ) S_o(\omega) = S_i(\omega) \cdot C(\omega) So(ω)=Si(ω)⋅C(ω)。
- 特例：加性==高斯白噪声（AWGN）==信道 。此时 C ( ω ) = K C(\omega) = K C(ω)=K（常数），信号仅经历固定的幅度衰减（ K K K）和加性噪声。
  r ( t ) = K ⋅ s i ( t ) + n ( t ) r(t) = K \cdot s_i(t) + n(t) r(t)=K⋅si(t)+n(t)
随参信道 ： f [ ⋅ ] f[\cdot] f[⋅] 是一个线性时变滤波器 ，其特性可以表示为 c ( t , τ ) c(t, \tau) c(t,τ) 或 C ( ω , τ ) C(\omega, \tau) C(ω,τ)，具有时变的衰减和时延。

1.3 编码信道数学模型

编码信道是研究数字信号编码/译码过程的信道模型，其特性用转移概率来描述。

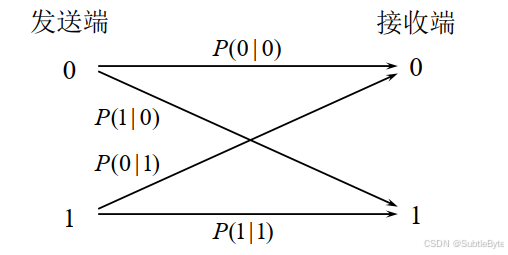
以二进制信道为例：

发送符号集 X = { 0 , 1 } X = \{0, 1\} X={0,1}，接收符号集 Y = { 0 , 1 } Y = \{0, 1\} Y={0,1}。
转移概率 P ( y ∣ x ) P(y|x) P(y∣x) 表示发送 x x x 而接收为 y y y 的概率。
- P ( 0 ∣ 0 ) P(0|0) P(0∣0) 和 P ( 1 ∣ 1 ) P(1|1) P(1∣1) 为正确转移概率。
- P ( 1 ∣ 0 ) P(1|0) P(1∣0) 和 P ( 0 ∣ 1 ) P(0|1) P(0∣1) 为错误转移概率。

发送端接收端 0 → P ( 0 ∣ 0 ) 0 → P ( 1 ∣ 0 ) 1 → P ( 0 ∣ 1 ) 1 → P ( 1 ∣ 1 ) \begin{array}{ccc} \text{发送端} & & \text{接收端} \\ 0 & \xrightarrow{P(0|0)} & 0 \\ & \xrightarrow{P(1|0)} & \\ 1 & \xrightarrow{P(0|1)} & 1 \\ & \xrightarrow{P(1|1)} & \\ \end{array} 发送端01P(0∣0) P(1∣0) P(0∣1) P(1∣1) 接收端01

系统的误码率 P e P_e Pe 为：
P e = P ( 0 ) ⋅ P ( 1 ∣ 0 ) + P ( 1 ) ⋅ P ( 0 ∣ 1 ) P_e = P(0) \cdot P(1|0) + P(1) \cdot P(0|1) Pe=P(0)⋅P(1∣0)+P(1)⋅P(0∣1)

无记忆信道：前后码元发生的错误相互独立。
有记忆信道：一个码元发生的错误与前后码元有关，需用马尔可夫链描述。

2. 恒参信道的传输特性

2.1 理想恒参信道特性

理想恒参信道是无失真传输信道，可等效为一个线性时不变网络。

无失真传输条件（时域）：即输入输出波形结构一致，只是幅度和出现时间不同
s o ( t ) = K ⋅ s i ( t − t d ) s_o(t) = K \cdot s_i(t - t_d) so(t)=K⋅si(t−td)

K K K：固定的幅度衰减（或放大）因子。
t d t_d td：固定的信号时延。

相应的频率响应函数 H ( ω ) H(\omega) H(ω) 为：
H ( ω ) = K e − j ω t d H(\omega) = K e^{-j\omega t_d} H(ω)=Ke−jωtd

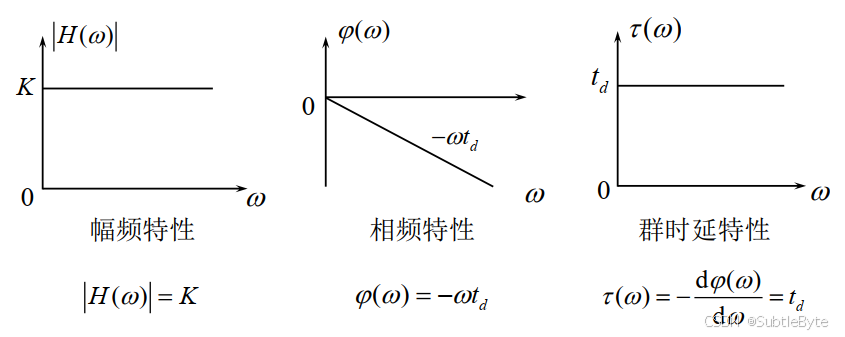
其特性为：

幅频特性 ： ∣ H ( ω ) ∣ = K |H(\omega)| = K ∣H(ω)∣=K（常数），所有频率分量获得相同的增益或衰减。
相频特性 ： φ ( ω ) = − ω t d \varphi(\omega) = -\omega t_d φ(ω)=−ωtd，相位与频率呈线性关系。
群时延特性 ： τ ( ω ) = − d φ ( ω ) d ω = t d \tau(\omega) = -\frac{d\varphi(\omega)}{d\omega} = t_d τ(ω)=−dωdφ(ω)=td（常数），所有频率分量具有相同的时延。

无失真传输要求振幅特性与频率无关，即其振幅一频率特性曲线是一条水平直线；要求其相位特性是一条通过原点的直线，或者等效地要求其传输群时延与频率无关，等于常数。

冲激响应 ： h ( t ) = K δ ( t − t d ) h(t) = K \delta(t - t_d) h(t)=Kδ(t−td)。

2.2 实际恒参信道特性

实际恒参信道无法完全满足无失真条件，主要存在以下线性失真：

幅频失真 ： ∣ H ( ω ) ∣ ≠ K |H(\omega)| \neq K ∣H(ω)∣=K。不同频率分量受到不同的衰减或放大。
相频失真（群时延失真） ： φ ( ω ) ≠ − ω t d \varphi(\omega) \neq -\omega t_d φ(ω)=−ωtd，或 τ ( ω ) ≠ t d \tau(\omega) \neq t_d τ(ω)=td。不同频率分量到达输出端的时间不一致。

以上失真不产生新的频率分量，因此均为线性失真

影响：

若信道的振幅---频率特性不理想，则信号发生的失真称为频率失真。

信道的相位特性不理想将使信号产生相位失真

对模拟信号：幅频失真会导致波形失真，导致信噪比下降；相位失真：对于语音信号，人耳对相位失真不敏感，但对视频信号影响大。
对数字信号 ：幅度失真和相位失真都会引起引起码间串扰（ISI），导致误码率升高。
幅度失真和相位失真也是一种线性失真，所以也可以用一个线性网络进行补偿。

改善措施 ：采用均衡技术，使信道的总传输特性逼近无失真条件。（后面会了解）

3. 随参信道的传输特性

3.1 随参信道的特点

传输特性时变 ：衰减和时延随机快速变化。
多径传播 ：信号经过多条路径到达接收端，各路径具有时变的衰减和时延。多径传播对信号的影响称为多径效应

3.2 多径传播的影响

平坦衰落（瑞利衰落）

考虑发送一个单频正弦波： s ( t ) = A cos ⁡ ω c t s(t) = A \cos \omega_c t s(t)=Acosωct。

经过 n n n 条路径传播后，接收信号为：
r ( t ) = ∑ i = 1 n a i ( t ) cos ⁡ [ ω c t + φ i ( t ) ] r(t) = \sum_{i=1}^{n} a_i(t) \cos[\omega_c t + \varphi_i(t)] r(t)=i=1∑nai(t)cos[ωct+φi(t)]

其中 a i ( t ) a_i(t) ai(t) 和 φ i ( t ) = − ω c τ i ( t ) \varphi_i(t) = -\omega_c \tau_i(t) φi(t)=−ωcτi(t) 是第 i i i 条路径的时变幅度和相位。

将 r ( t ) r(t) r(t) 表示为窄带形式：
r ( t ) = X ( t ) cos ⁡ ω c t − Y ( t ) sin ⁡ ω c t = V ( t ) cos ⁡ [ ω c t + φ ( t ) ] r(t) = X(t) \cos \omega_c t - Y(t) \sin \omega_c t = V(t) \cos[\omega_c t + \varphi(t)] r(t)=X(t)cosωct−Y(t)sinωct=V(t)cos[ωct+φ(t)]

其中：

同相分量： X ( t ) = ∑ i = 1 n a i ( t ) cos ⁡ φ i ( t ) X(t) = \sum_{i=1}^{n} a_i(t) \cos \varphi_i(t) X(t)=∑i=1nai(t)cosφi(t)
正交分量： Y ( t ) = ∑ i = 1 n a i ( t ) sin ⁡ φ i ( t ) Y(t) = \sum_{i=1}^{n} a_i(t) \sin \varphi_i(t) Y(t)=∑i=1nai(t)sinφi(t)
随机包络： V ( t ) = X 2 ( t ) + Y 2 ( t ) V(t) = \sqrt{X^2(t) + Y^2(t)} V(t)=X2(t)+Y2(t)
随机相位： φ ( t ) = arctan ⁡ [ Y ( t ) / X ( t ) ] \varphi(t) = \arctan[Y(t)/X(t)] φ(t)=arctan[Y(t)/X(t)]

结论：在大量路径的情况下， X ( t ) X(t) X(t) 和 Y ( t ) Y(t) Y(t) 是大量独立随机变量之和。根据中心极限定理，它们近似为零均值高斯过程。因此：

包络 V ( t ) V(t) V(t) 服从瑞利分布。
相位 φ ( t ) \varphi(t) φ(t) 服从均匀分布。

影响

信号的频谱由一根谱线扩散为一个窄带频谱，称为频率弥散。

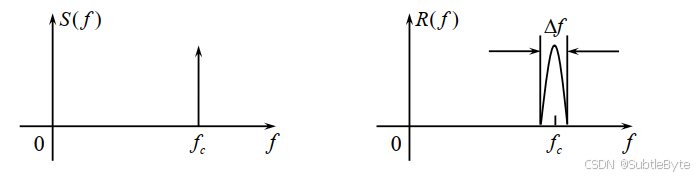
单一频率的信号变成了包络和相位随机缓变的窄带信号，称为瑞利衰落 或平坦衰落

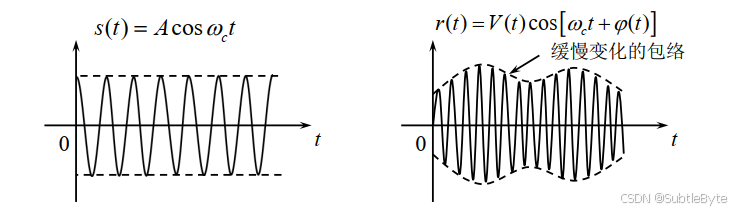
频率选择性衰落

考虑一个简化的两径模型 ：两条路径幅度衰减相同（ K K K），相对时延差为 τ \tau τ。

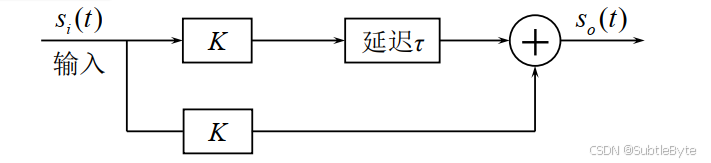
信道输出：
s o ( t ) = K s i ( t ) + K s i ( t − τ ) S o ( ω ) = K S i ( ω ) + K S i ( ω ) e − j ω τ = K S i ( ω ) ( 1 + e − j ω τ ) s_o(t) = K s_i(t) + K s_i(t - \tau)\\ S_{o}(\omega)=K S_{i}(\omega)+K S_{i}(\omega) e^{-j \omega \tau}=K S_{i}(\omega)\left(1+e^{-j \omega \tau}\right) so(t)=Ksi(t)+Ksi(t−τ)So(ω)=KSi(ω)+KSi(ω)e−jωτ=KSi(ω)(1+e−jωτ)

频率响应：
H ( ω ) = s o ( t ) s i ( t ) = K ( 1 + e − j ω τ ) = 2 K cos ⁡ ( ω τ 2 ) e − j ω τ 2 H(\omega) = \frac{s_o(t)}{s_i(t)} =K(1 + e^{-j\omega\tau}) = 2K \cos\left(\frac{\omega\tau}{2}\right) e^{-j\frac{\omega\tau}{2}} H(ω)=si(t)so(t)=K(1+e−jωτ)=2Kcos(2ωτ)e−j2ωτ

幅频特性：
∣ H ( ω ) ∣ = 2 K ∣ cos ⁡ ( ω τ 2 ) ∣ |H(\omega)| = 2K \left| \cos\left(\frac{\omega\tau}{2}\right) \right| ∣H(ω)∣=2K cos(2ωτ)

幅频特性随频率变化曲线：

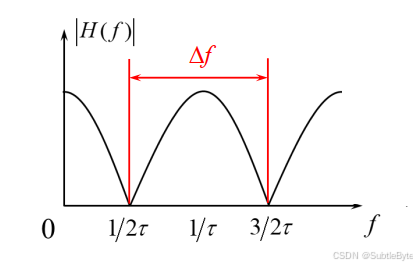
结论：

幅频特性随频率变化，在某些频率点出现传输零点，这意味着信号中不同频率分量受到不同程度的衰减，且这种衰减随时间（时延 τ \tau τ变化）变化，称为频率选择性衰落。
实际的多径信道中通常有不止两条路径，并且每条路径的信号衰减一般也不相同，所以不会出现图中的零点。但是，接收信号的包络肯定会出现随机起伏 (random fluctuation) 。这时，设 τ m a x \tau_{max} τmax为多径中最大的相对时延差，

相关带宽：

定义：相邻传输零点的频率间隔。对于两径模型， Δ f = 1 τ \Delta f = \frac{1}{\tau} Δf=τ1。
推广：对于多径信道，最大多径时延差为 τ max ⁡ \tau_{\max} τmax，则相关带宽 Δ f ≈ 1 τ max ⁡ \Delta f \approx \frac{1}{\tau_{\max}} Δf≈τmax1。
设计准则 ：为避免严重的频率选择性衰落，信号带宽 B s B_s Bs 应小于信道的相关带宽 Δ f \Delta f Δf： B s < Δ f B_s < \Delta f Bs<Δf。工程上通常取：
B s = ( 1 3 ∼ 1 5 ) Δ f B_s = \left( \frac{1}{3} \sim \frac{1}{5} \right) \Delta f Bs=(31∼51)Δf
相应的码元宽度 T B T_B TB 应满足： T B = ( 3 ∼ 5 ) τ max ⁡ T_B = (3 \sim 5) \tau_{\max} TB=(3∼5)τmax。

抗衰落技术

多径效应会使数字信号的码间串扰增大。为了减小码间串扰的影响，通常要降低码元传输速率。因为，若码元速率降低，则信号带宽也将随之减小，多径效应的影响也随之减轻。

理解：

为什么多径效应会使码间串扰增大？

设发送的符号周期为 T s T_s Ts，多径信道的最大时延扩展为 τ m a x \tau_{max} τmax（即最长路径与最短路径的时延差）。

若 τ m a x \tau_{max} τmax接近或大于 T s T_s Ts，则前一个符号的延迟副本会落入当前符号的判决时刻，干扰当前符号的判决；同时，当前符号的延迟副本也会干扰后续符号

为什么码元速率降低，则信号带宽也将随之减小？

在后面的章节中我们会了解到数字系带传输和数字带通传输

基带传输 ：若采用理想的奈奎斯特脉冲成形，无码间串扰的最小理论带宽为 $B=R_{B} / 2 （为（为（为R_B 符号率，单位波特）。实际中采用升余弦滚降滤波器时，带宽为符号率，单位波特）。实际中采用升余弦滚降滤波器时，带宽为符号率，单位波特）。实际中采用升余弦滚降滤波器时，带宽为B=(1+\\alpha) R_{B} / 2 ，其中，其中，其中\\alpha$ 为滚降系数（ 0 ≤ α ≤ 1 0≤\alpha≤1 0≤α≤1）

带通调制（如PSK、QAM）：调制后的信号带宽通常是基带信号带宽的两倍（双边带），但实际中也常采用单边带或其它方式，带宽仍与符号率成正比

正交频分复用（OFDM）：将宽带信道划分为多个正交的窄带子信道，使每个子信道的带宽小于相关带宽，从而将频率选择性衰落转化为平坦衰落。
分集接收：从时间、频率、空间等多个维度获取同一信号的多个独立衰落副本，然后进行合并（如选择合并、等增益合并、最大比合并），以提高接收信号的信噪比。
其他技术：扩频、MIMO、均衡等。

4. 噪声与带宽

4.1 信道噪声

噪声是通信系统中不可避免的干扰，分类如下：

按来源：人为噪声、自然噪声、内部噪声（如热噪声）。
按性质 ：
- 脉冲噪声：突发、持续时间短、幅度大。
- 窄带/单频噪声：单一频率或窄带。
- 起伏噪声 ：普遍存在、持续、功率谱密度平坦（白噪声）、瞬时值服从高斯分布。是通信系统噪声分析的主要对象，包括热噪声、散弹噪声、宇宙噪声。

热噪声：

来源于电阻性元器件中电子的热运动。
功率谱密度在极宽频率范围（ 0 ∼ 10 12 Hz 0 \sim 10^{12} \text{ Hz} 0∼1012 Hz）内均匀分布，可视为白噪声。
瞬时电压值服从高斯分布，均值为0。
因此，热噪声常被建模为零均值高斯白噪声，其概率密度函数和功率谱密度为：
f n ( v ) = 1 2 π σ n e − v 2 2 σ n 2 , P n ( f ) = n 0 2 (W/Hz, 双边) f_n(v) = \frac{1}{\sqrt{2\pi}\sigma_n} e^{-\frac{v^2}{2\sigma_n^2}}, \quad P_n(f) = \frac{n_0}{2} \text{ (W/Hz, 双边)} fn(v)=2π σn1e−2σn2v2,Pn(f)=2n0 (W/Hz, 双边)

4.2 等效噪声带宽

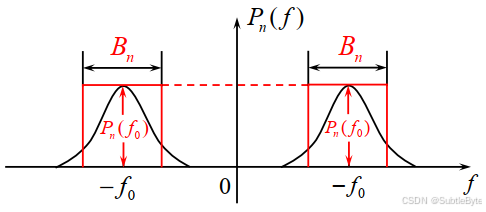
对于一个频率响应为 H ( f ) H(f) H(f) 的带通系统，其等效噪声带宽 B n B_n Bn 定义为：
B n = ∫ 0 + ∞ ∣ H ( f ) ∣ 2 d f ∣ H ( f 0 ) ∣ 2 = ∫ − ∞ + ∞ ∣ H ( f ) ∣ 2 d f 2 ∣ H ( f 0 ) ∣ 2 B_n = \frac{\int_{0}^{+\infty} |H(f)|^2 df}{|H(f_0)|^2} = \frac{\int_{-\infty}^{+\infty} |H(f)|^2 df}{2|H(f_0)|^2} Bn=∣H(f0)∣2∫0+∞∣H(f)∣2df=2∣H(f0)∣2∫−∞+∞∣H(f)∣2df

其中 f 0 f_0 f0 是中心频率（通常取幅频响应最大值对应的频率）。

物理意义 ：一个宽度为 B n B_n Bn、高度为 ∣ H ( f 0 ) ∣ 2 |H(f_0)|^2 ∣H(f0)∣2 的理想矩形滤波器，所通过的噪声功率与实际滤波器相同。后续分析中，常使用等效噪声带宽来简化计算。

理解：

热噪声本身是白色的。但是，在通信系统接收端解调器中对信号解调时，叠加在信号上的热噪声已经经过了接收机带通滤波器的过滤，从而其带宽受到了限制，故它巳经不是白色的了，成为了窄带噪声或称为带限 (band - limited) 白噪声 。由于滤波器是一种线性电路，高斯过程通过线性电路后，仍为高斯过程，故此窄带噪声又常称为窄带高斯噪声。

设经过接收滤波器后的噪声双边功率谱密度如图所示，为了描述窄带噪声的带宽，我们引入噪声等效带宽 (equivalent bandwidth) 的概念。这时，将噪声功率谱密度曲线的形状变为矩形（见图中虚线），并保持噪声功率不变

4.3 各类带宽概念

由于信号能量通常集中在有限频带，定义了多种带宽度量：

绝对带宽（Absolute Bandwidth）：信号频谱非零部分占据的整个频率范围。
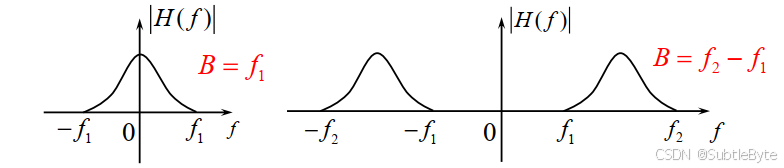
3dB带宽（半功率带宽，Half-Power Bandwidth） ：功率谱密度（或幅频响应平方）下降到峰值一半（即幅度下降至 1 / 2 ≈ 0.707 1/\sqrt{2} \approx 0.707 1/2 ≈0.707）时所对应的频率间隔。
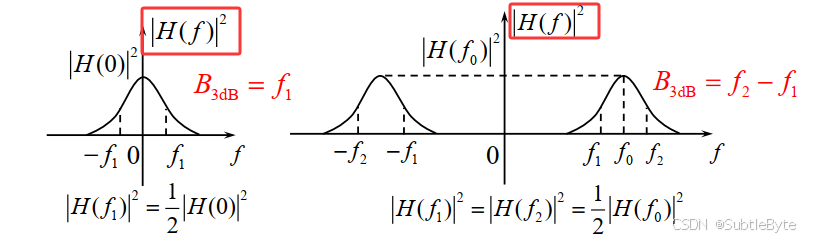
等效噪声带宽（Equivalent Bandwidth）：如上节定义，用于噪声功率计算。
谱零点带宽（Null-to-Null Bandwidth）：信号功率谱主瓣（第一个零点之间）的宽度
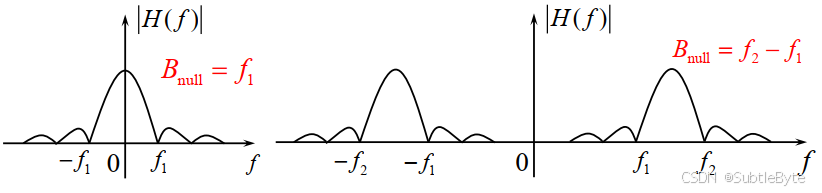
6dB带宽（半幅度带宽，Half-Amplitude Bandwidth） ：幅频响应下降到峰值一半（即下降6dB）时所对应的频率间隔。

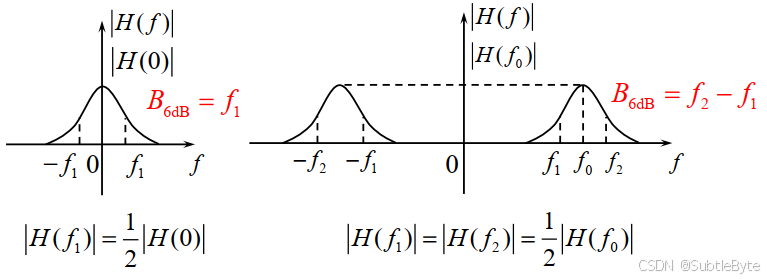
理解：

某些信号频带宽度无限延伸，无法设计出传输所有频率分量的信道，就算可以设计出来，传输所有频率分量有时也会产生资源的浪费。因为一个信号的信息一般只集中在一个有限频段内。因此我们可以根据信号能量（功率）集中的情况，恰当的定义带宽

5. 信道容量

信道容量是指信道能够传输的最大平均信息速率

5.1 离散信道的信道容量

离散信道的输入 X X X 和输出 Y Y Y 均为离散随机变量。

互信息与平均互信息

互信息 I ( x i ; y j ) I(x_i; y_j) I(xi;yj)：收到 y j y_j yj后，关于 x i x_i xi的不确定度的减少量。
I ( x i ; y j ) = I ( x i ) − I ( x i ∣ y i ) = log ⁡ 2 P ( x i ∣ y j ) P ( x i ) = log ⁡ 2 P ( y j ∣ x i ) P ( y j ) I(x_i; y_j) = I(x_i) - I(x_i|y_i) = \log_2 \frac{P(x_i|y_j)}{P(x_i)} = \log_2 \frac{P(y_j|x_i)}{P(y_j)} I(xi;yj)=I(xi)−I(xi∣yi)=log2P(xi)P(xi∣yj)=log2P(yj)P(yj∣xi)
- I ( x i ) I(x_i) I(xi)：收到 y j y_j yj前，对 x i x_i xi的不确定度。
- I ( x i ∣ y j ) I(x_i∣y_j) I(xi∣yj)：收到 y j y_j yj后，对 x i x_i xi仍存在的不确定度。
- I ( x i ; y j ) I(x_i;y_j) I(xi;yj)：收到 y j y_j yj后，对 x i x_i xi不确定度的减少量，即获得的信息量。
平均互信息 I ( X ; Y ) I(X; Y) I(X;Y)：互信息的统计平均，表示接收端 Y Y Y 对发送端 X X X 的平均不确定度的减少量。
I ( X ; Y ) = H ( X ) − H ( X ∣ Y ) = H ( Y ) − H ( Y ∣ X ) I(X; Y) = H(X) - H(X|Y) = H(Y) - H(Y|X) I(X;Y)=H(X)−H(X∣Y)=H(Y)−H(Y∣X)

其中 H ( X ) H(X) H(X) 为信源熵， H ( X ∣ Y ) H(X|Y) H(X∣Y) 为条件熵。
- H ( X ) H(X) H(X)：发送符号 X X X的信息熵，表示发送前的平均不确定度。
- H ( X ∣ Y ) H(X|Y) H(X∣Y)：条件熵 ，表示收到 Y Y Y后对仍然 X X X存在的平均不确定度。

理解：

在第一章信息的度量这一小节中，我们了解到了自信息的概念，下面做一个简单的回顾：

为了定量表征信息，度量事件发生所提供的信息量大小，引入自信息 I ( x i ) I(x_i) I(xi)。信息量大小与该事件发生的不确定性有关。

自信息 I ( x i ) I(x_i) I(xi) 是事件概率 p ( x i ) p(x_i) p(xi) 的函数： I ( x i ) = f [ p ( x i ) ] I(x_i) = f[p(x_i)] I(xi)=f[p(xi)]。

自信息量的计算公式为概率倒数的对数，满足以上性质的函数定义为： I ( x i ) = log ⁡ a 1 p ( x i ) = − log ⁡ a p ( x i ) I(x_i) = \log_a \frac{1}{p(x_i)} = -\log_a p(x_i) I(xi)=logap(xi)1=−logap(xi)

自信息量的单位取决于对数底 a a a，一般 a = 2 a=2 a=2

平均互信息的推导：
I ( X ; Y ) = E [ I ( x i ; y j ) ] = E [ I ( x i ) − I ( x i ∣ y j ) ] = E [ I ( x i ) ] − E [ I ( x i ∣ y j ) ] = ∑ i = 1 n P ( x i ) log ⁡ 2 1 P ( x i ) − ∑ i = 1 n ∑ j = 1 m P ( x i y j ) log ⁡ 2 1 P ( x i ∣ y j ) = ∑ i = 1 n P ( x i ) log ⁡ 2 1 P ( x i ) − ∑ j = 1 m P ( y j ) ∑ i = 1 n P ( x i ∣ y j ) log ⁡ 2 1 P ( x i ∣ y j ) = H ( X ) − H ( X ∣ Y ) \begin{aligned} I(X ; Y) & =E\left[I\left(x_{i} ; y_{j}\right)\right]=E\left[I\left(x_{i}\right)-I\left(x_{i} \mid y_{j}\right)\right]=E\left[I\left(x_{i}\right)\right]-E\left[I\left(x_{i} \mid y_{j}\right)\right] \\ & =\sum_{i=1}^{n} P\left(x_{i}\right) \log {2} \frac{1}{P\left(x{i}\right)}-\sum_{i=1}^{n} \sum_{j=1}^{m} P\left(x_{i} y_{j}\right) \log {2} \frac{1}{P\left(x{i} \mid y_{j}\right)} \\ & =\sum_{i=1}^{n} P\left(x_{i}\right) \log {2} \frac{1}{P\left(x{i}\right)}-\sum_{j=1}^{m} P\left(y_{j}\right) \sum_{i=1}^{n} P\left(x_{i} \mid y_{j}\right) \log {2} \frac{1}{P\left(x{i} \mid y_{j}\right)} \\ & =H(X)-H(X \mid Y) \end{aligned} I(X;Y)=E[I(xi;yj)]=E[I(xi)−I(xi∣yj)]=E[I(xi)]−E[I(xi∣yj)]=i=1∑nP(xi)log2P(xi)1−i=1∑nj=1∑mP(xiyj)log2P(xi∣yj)1=i=1∑nP(xi)log2P(xi)1−j=1∑mP(yj)i=1∑nP(xi∣yj)log2P(xi∣yj)1=H(X)−H(X∣Y)

信道容量定义

离散信道的信道容量定义为：在最佳输入分布下，平均互信息的最大值。

单位：比特/符号（bit/symbol）
C = max ⁡ P ( x ) I ( X ; Y ) = max ⁡ P ( x ) [ H ( X ) − H ( X ∣ Y ) ] C = \max_{P(x)} I(X; Y) = \max_{P(x)} [H(X) - H(X|Y)] C=P(x)maxI(X;Y)=P(x)max[H(X)−H(X∣Y)]
单位：比特/秒（bit/s）
C t = max ⁡ P ( x ) { r ⋅ [ H ( X ) − H ( X ∣ Y ) ] } C_t = \max_{P(x)} \{ r \cdot [H(X) - H(X|Y)] \} Ct=P(x)max{r⋅[H(X)−H(X∣Y)]}

其中 r r r 为符号传输速率（符号/秒）。

离散二进制对称信道的信道容量

离散信道有很多种类型，求解信道容量以及对应的最佳输入概率方法不一，有的还很复杂。在这里给出一个特殊的例子：离散二进制对称信道

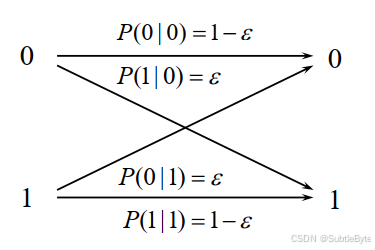
令：

正确的传递概率： P ( 0 ∣ 0 ) = P ( 1 ∣ 1 ) = 1 − ε P(0|0) = P(1|1) = 1 - \varepsilon P(0∣0)=P(1∣1)=1−ε
错误的传递概率： P ( 1 ∣ 0 ) = P ( 0 ∣ 1 ) = ε P(1|0) = P(0|1) = \varepsilon P(1∣0)=P(0∣1)=ε

输入等概：
P ( x = 0 ) = P ( x = 1 ) = 1 2 P(x=0)=P(x=1)=\frac{1}{2} P(x=0)=P(x=1)=21

输出概率为：
P ( y = 0 ) = P ( 0 ) P ( 0 ∣ 0 ) + P ( 1 ) P ( 0 ∣ 1 ) = 1 2 ( 1 − ε ) + 1 2 ε = 1 2 P ( y = 1 ) = P ( 0 ) P ( 1 ∣ 0 ) + P ( 1 ) P ( 1 ∣ 1 ) = 1 2 ( 1 − ε ) + 1 2 ε = 1 2 P(y=0)=P(0) P(0 \mid 0)+P(1) P(0 \mid 1)=\frac{1}{2}(1-\varepsilon)+\frac{1}{2} \varepsilon=\frac{1}{2}\\ P(y=1)=P(0) P(1 \mid 0)+P(1) P(1 \mid 1)=\frac{1}{2}(1-\varepsilon)+\frac{1}{2} \varepsilon=\frac{1}{2} P(y=0)=P(0)P(0∣0)+P(1)P(0∣1)=21(1−ε)+21ε=21P(y=1)=P(0)P(1∣0)+P(1)P(1∣1)=21(1−ε)+21ε=21

有次我们可知：当输入等概，输出也等概

此外还有以下性质：

输入等概时，转移概率等于后验概率
对称信道的条件熵与输入分布无关，为定值。 H ( Y ) = log ⁡ 2 2 = 1 b i t / 符号 H(Y)=\log_{2}2=1bit/符号 H(Y)=log22=1bit/符号符号为最大熵
达到信道容量的最佳输入分布为等概分布
条件熵 H ( X ∣ Y ) = H ( Y ∣ X ) H(X|Y)=H(Y|X) H(X∣Y)=H(Y∣X)

5.2 连续信道的信道容量

奈奎斯特定理（无扰信道）

对于带宽为 B B B Hz 的无噪声信道，若信号采用 M M M 进制电平，则最大信息传输速率（信道容量）为：
C t = 2 B log ⁡ 2 M ( bit/s ) C_t = 2B \log_2 M \ (\text{bit/s}) Ct=2Blog2M (bit/s)

香农公式（有扰信道）

对于带宽为 B B B Hz、加性高斯白噪声（功率 N N N，单边功率谱密度 n 0 n_0 n0）的连续信道，其信道容量为：
C t = B log ⁡ 2 ( 1 + S N ) = B log ⁡ 2 ( 1 + S n 0 B ) ( bit/s ) C_t = B \log_2 \left( 1 + \frac{S}{N} \right) = B \log_2 \left( 1 + \frac{S}{n_0 B} \right) \ (\text{bit/s}) Ct=Blog2(1+NS)=Blog2(1+n0BS) (bit/s)

S S S：信号平均功率（W）
N = n 0 B N = n_0 B N=n0B：噪声功率（W）

香农公式的结论与应用

三要素 ： C t C_t Ct 由 B B B、 S S S、 n 0 n_0 n0 决定。
带宽与信噪比的互换：
- 给定 C t C_t Ct，可通过增加带宽 B B B 来降低所需的信噪比 S N \frac{S}{N} NS（适用于功率受限的深空通信，如扩频）。
- 也可通过提高信噪比来节省带宽（适用于频带受限的有线通信）。
- 带宽 B B B 一定，增大 S S S 或者减小 n 0 n_0 n0（即提高信噪比），可以增大 C t C_t Ct
极限容量 ：当带宽 B → ∞ B \to \infty B→∞ 时， C t C_t Ct 趋于一个极限值，这个值称为信道容量极限：
lim ⁡ B → ∞ C t = S n 0 log ⁡ 2 e ≈ 1.44 S n 0 ( bit/s ) \lim_{B \to \infty} C_t = \frac{S}{n_0} \log_2 e \approx 1.44 \frac{S}{n_0} \ (\text{bit/s}) B→∞limCt=n0Slog2e≈1.44n0S (bit/s)

证明：
lim ⁡ B → ∞ C t = lim ⁡ B → ∞ B log ⁡ 2 ( 1 + S n 0 B ) = lim ⁡ B → ∞ S n 0 ⋅ n 0 B S log ⁡ 2 ( 1 + S n 0 B ) = S n 0 lim ⁡ B → ∞ log ⁡ 2 ( 1 + S n 0 B ) n 0 B S = S n 0 lim ⁡ x → ∞ log ⁡ 2 ( 1 + 1 x ) x = S n 0 log ⁡ 2 e ≈ 1.44 S n 0 \begin{aligned} \lim {B \rightarrow \infty} C{t} & =\lim {B \rightarrow \infty} B \log {2}\left(1+\frac{S}{n{0} B}\right)=\lim {B \rightarrow \infty} \frac{S}{n{0}} \cdot \frac{n{0} B}{S} \log {2}\left(1+\frac{S}{n{0} B}\right) \\ & =\frac{S}{n_{0}} \lim {B \rightarrow \infty} \log {2}\left(1+\frac{S}{n{0} B}\right)^{\frac{n{0} B}{S}} \\ & =\frac{S}{n_{0}} \lim _{x \rightarrow \infty} \log {2}\left(1+\frac{1}{x}\right)^{x} \\ & =\frac{S}{n{0}} \log {2} e \approx 1.44 \frac{S}{n{0}} \end{aligned} B→∞limCt=B→∞limBlog2(1+n0BS)=B→∞limn0S⋅Sn0Blog2(1+n0BS)=n0SB→∞limlog2(1+n0BS)Sn0B=n0Sx→∞limlog2(1+x1)x=n0Slog2e≈1.44n0S
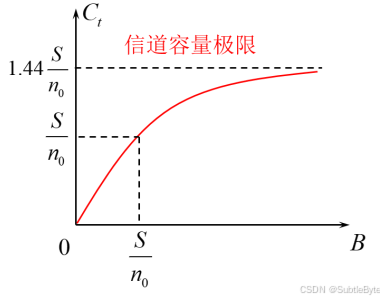
信道编码定理 ：只要信息速率 R b < C t R_b < C_t Rb<Ct，总存在一种编码方式，使得误码率任意小；若 R b > C t R_b > C_t Rb>Ct，则不可能实现无差错传输。

例题

例题2 ：设一幅黑白数字相片有400万个像素，每个像素有16个等概亮度电平。用3kHz带宽、信噪比20dB的信道传输，求所需时间。
解：
- 图片信息量： I = 4 × 10 6 × log ⁡ 2 16 = 1.6 × 10 7 bit I = 4 \times 10^6 \times \log_2 16 = 1.6 \times 10^7 \ \text{bit} I=4×106×log216=1.6×107 bit。

信道容量： 20 dB = 100 20 \text{dB} = 100 20dB=100（倍）， C t = 3000 × log ⁡ 2 ( 1 + 100 ) ≈ 3000 × 6.66 = 19980 bit/s C_t = 3000 \times \log_2 (1+100) \approx 3000 \times 6.66 = 19980 \ \text{bit/s} Ct=3000×log2(1+100)≈3000×6.66=19980 bit/s。
注意：

dB的换算是基于对数关系的，主要有两种公式：功率比值用10倍对数，电压/声压等场量比值用20倍对数
- d B = 10 lg ⁡ ( P 1 P 2 ) dB = 10 \lg (\frac{P_1}{P_2}) dB=10lg(P2P1)
- d B = 20 lg ⁡ ( V 1 V 2 ) dB = 20 \lg (\frac{V_1}{V_2}) dB=20lg(V2V1)
- 传输时间： T = I / C t ≈ 800.8 s T = I / C_t \approx 800.8 \ \text{s} T=I/Ct≈800.8 s。

例题3 ：带宽1MHz，信噪比63，求合适的信息速率 R b R_b Rb 和信号电平数 M M M。
解：
- 信道容量： C t = 10 6 × log ⁡ 2 ( 1 + 63 ) = 10 6 × 6 = 6 Mbit/s C_t = 10^6 \times \log_2 (1+63) = 10^6 \times 6 = 6 \ \text{Mbit/s} Ct=106×log2(1+63)=106×6=6 Mbit/s。
- 合适的信息速率 R b R_b Rb 应小于 C t C_t Ct，可取 R b = 5 Mbit/s R_b = 5 \ \text{Mbit/s} Rb=5 Mbit/s。
- 根据奈氏准则，最大符号率 R s = 2 B = 2 MBaud R_s = 2B = 2 \ \text{MBaud} Rs=2B=2 MBaud。
- 所需电平数： M = 2 R b / R s = 2 5 / 2 = 2 2.5 ≈ 5.66 M = 2^{R_b / R_s} = 2^{5/2} = 2^{2.5} \approx 5.66 M=2Rb/Rs=25/2=22.5≈5.66，取 M = 4 M=4 M=4 或 8 8 8（需检查是否满足 R b ≤ C t R_b \leq C_t Rb≤Ct）。
  - d B = 20 lg ⁡ ( V 1 V 2 ) dB = 20 \lg (\frac{V_1}{V_2}) dB=20lg(V2V1)
- 传输时间： T = I / C t ≈ 800.8 s T = I / C_t \approx 800.8 \ \text{s} T=I/Ct≈800.8 s。

笔记总结内容来自：通信原理主讲：张锦皓 https://www.bilibili.com/video/BV1wA4y1f7Co?vd_source=a9099c2bbd4e16de0bbe08d30051754a