四旋翼飞行器轨迹跟踪仿真控制路径规划与轨迹优化MATLAB四旋翼飞行器仿真无人机simul...

四旋翼飞行器轨迹跟踪仿真控制路径规划与轨迹优化MATLAB四旋翼飞行器仿真无人机simulink有公式说明文档

最近在研究四旋翼飞行器的轨迹跟踪问题，发现这玩意儿还挺有意思的。今天就和大家分享一下我在MATLAB和Simulink里做的一些仿真实验，顺便聊聊控制算法和路径规划的那些事儿。

首先，四旋翼飞行器的动力学模型是绕不开的。简单来说，四旋翼的运动可以用以下公式来描述：

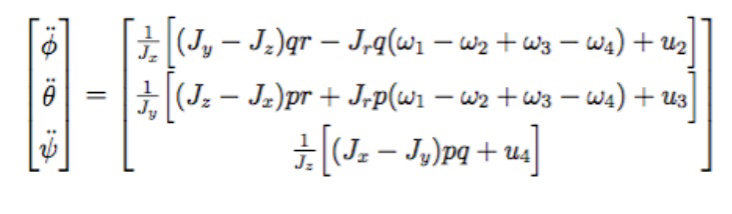
\ddot{x} = \frac{u}{m} (\cos \phi \sin \theta \cos \psi + \sin \phi \sin \psi)

\ddot{y} = \frac{u}{m} (\cos \phi \sin \theta \sin \psi - \sin \phi \cos \psi)

四旋翼飞行器轨迹跟踪仿真控制路径规划与轨迹优化MATLAB四旋翼飞行器仿真无人机simulink有公式说明文档

\ddot{z} = \frac{u}{m} \cos \phi \cos \theta - g

这里的 \(u\) 是总的推力，\(\phi\), \(\theta\), \(\psi\) 分别是滚转、俯仰和偏航角。看起来有点复杂，但其实核心思想就是通过控制这四个量来让飞行器按照我们想要的轨迹飞行。

接下来，我用MATLAB写了个简单的PID控制器来跟踪轨迹。代码如下：

matlab 复制代码

% PID控制器参数
Kp = 1.0;
Ki = 0.01;
Kd = 0.1;

% 初始化误差和积分项
error = 0;
integral = 0;
derivative = 0;
last_error = 0;

% 仿真时间步长
dt = 0.01;

% 目标轨迹
target_trajectory = [sin(2*pi*t); cos(2*pi*t)];

% 仿真循环
for t = 0:dt:10
    % 计算当前误差
    error = target_trajectory(t) - current_position(t);
    
    % 计算积分和微分项
    integral = integral + error * dt;
    derivative = (error - last_error) / dt;
    
    % 计算控制输出
    control_output = Kp * error + Ki * integral + Kd * derivative;
    
    % 更新上一次的误差
    last_error = error;
    
    % 应用控制输出到飞行器模型
    apply_control(control_output);
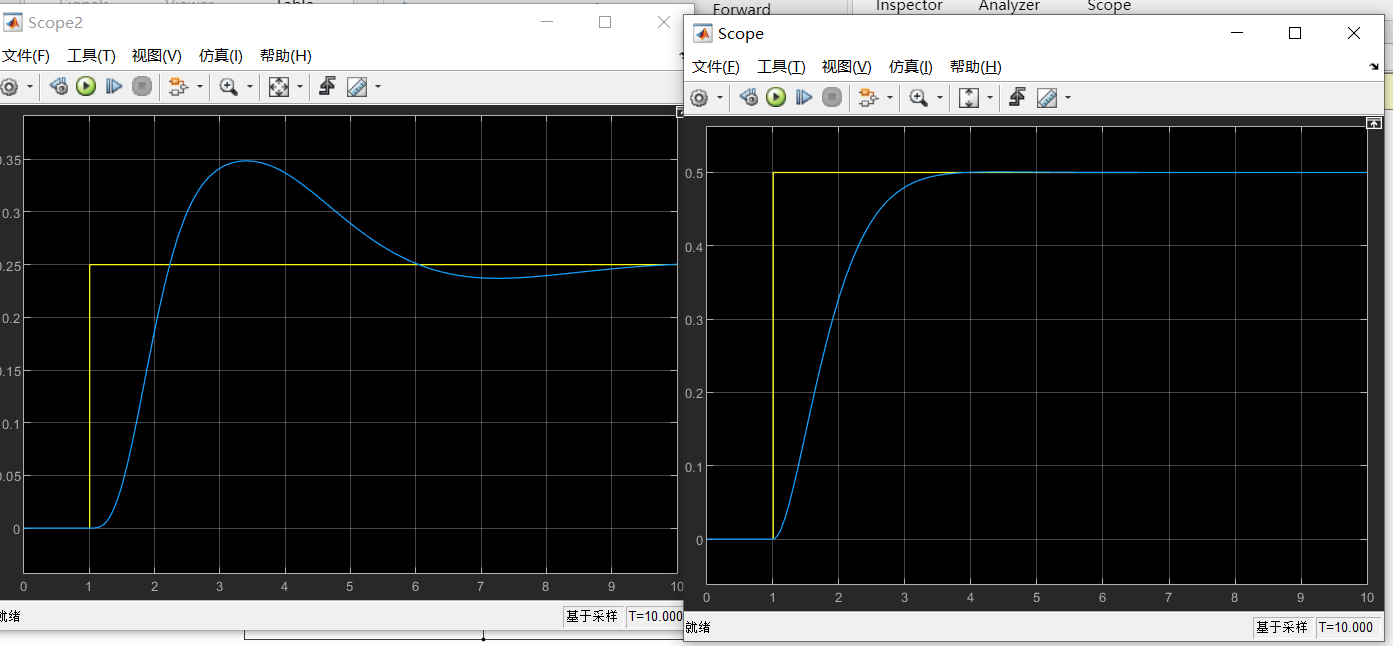
end

这段代码的核心就是一个经典的PID控制器。通过不断计算误差、积分和微分项，我们可以得到一个控制输出，然后把这个输出应用到飞行器模型上，让它尽可能地跟踪目标轨迹。

当然，PID控制器虽然简单，但在实际应用中可能会遇到一些问题，比如参数调优比较麻烦，或者在某些情况下响应不够快。这时候，我们可以考虑更高级的控制算法，比如LQR（线性二次调节器）或者MPC（模型预测控制）。

路径规划也是一个很有意思的话题。我们可以用一些优化算法来生成一条最优的飞行路径。比如，我写了个简单的A*算法来规划路径：

matlab 复制代码

function path = A_star(start, goal, map)
    % 初始化开放列表和关闭列表
    open_list = PriorityQueue();
    open_list.insert(start, 0);
    came_from = containers.Map('KeyType','double','ValueType','double');
    cost_so_far = containers.Map('KeyType','double','ValueType','double');
    cost_so_far(start) = 0;
    
    while ~isempty(open_list)
        current = open_list.pop();
        
        if current == goal
            break;
        end
        
        for next = neighbors(current, map)
            new_cost = cost_so_far(current) + distance(current, next);
            if ~isKey(cost_so_far, next) || new_cost < cost_so_far(next)
                cost_so_far(next) = new_cost;
                priority = new_cost + heuristic(goal, next);
                open_list.insert(next, priority);
                came_from(next) = current;
            end
        end
    end
    
    % 重建路径
    path = [];
    current = goal;
    while current ~= start
        path = [current; path];
        current = came_from(current);
    end
    path = [start; path];
end

这个A*算法的核心思想是通过启发式函数来估计从当前点到目标点的代价，然后选择代价最小的路径。虽然这里只是一个简单的二维地图，但同样的思路可以扩展到三维空间，用来规划无人机的飞行路径。

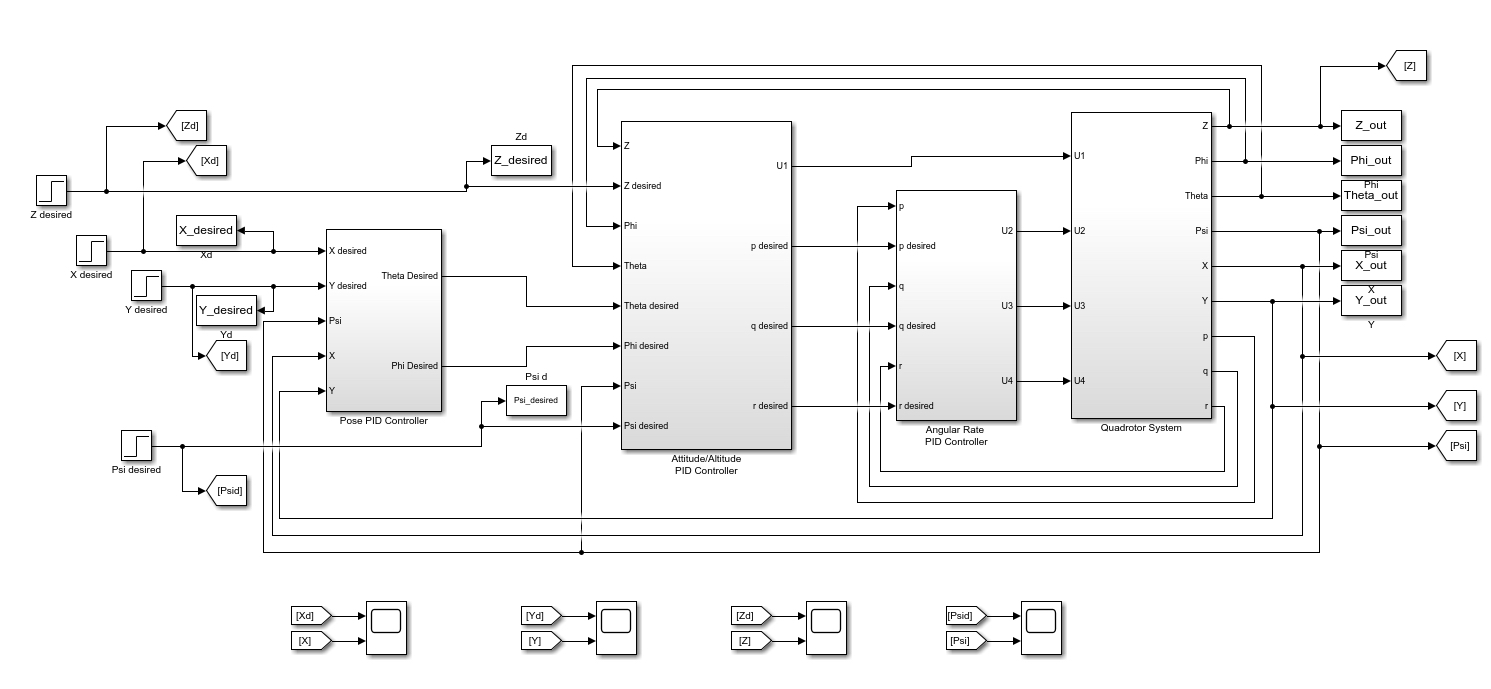
最后，我把这些控制算法和路径规划算法集成到了Simulink里，做了一个完整的四旋翼飞行器仿真模型。通过Simulink的图形化界面，我可以很方便地调整参数、观察仿真结果，甚至可以直接生成C代码，方便后续的硬件实现。

总的来说，四旋翼飞行器的轨迹跟踪和控制是一个很有意思的研究方向，涉及到了动力学建模、控制算法、路径规划等多个领域。虽然今天只是简单聊了一些基础的内容，但希望这些内容能对大家有所帮助。如果你对这个话题感兴趣，不妨自己动手试试，说不定会有更多的发现！

四旋翼飞行器轨迹跟踪仿真 控制 路径规划与轨迹优化MATLAB四旋翼飞行器仿真无人机simul...

四旋翼飞行器轨迹跟踪仿真控制路径规划与轨迹优化MATLAB四旋翼飞行器仿真无人机simul...