什么是四叉树(Quadtree)?
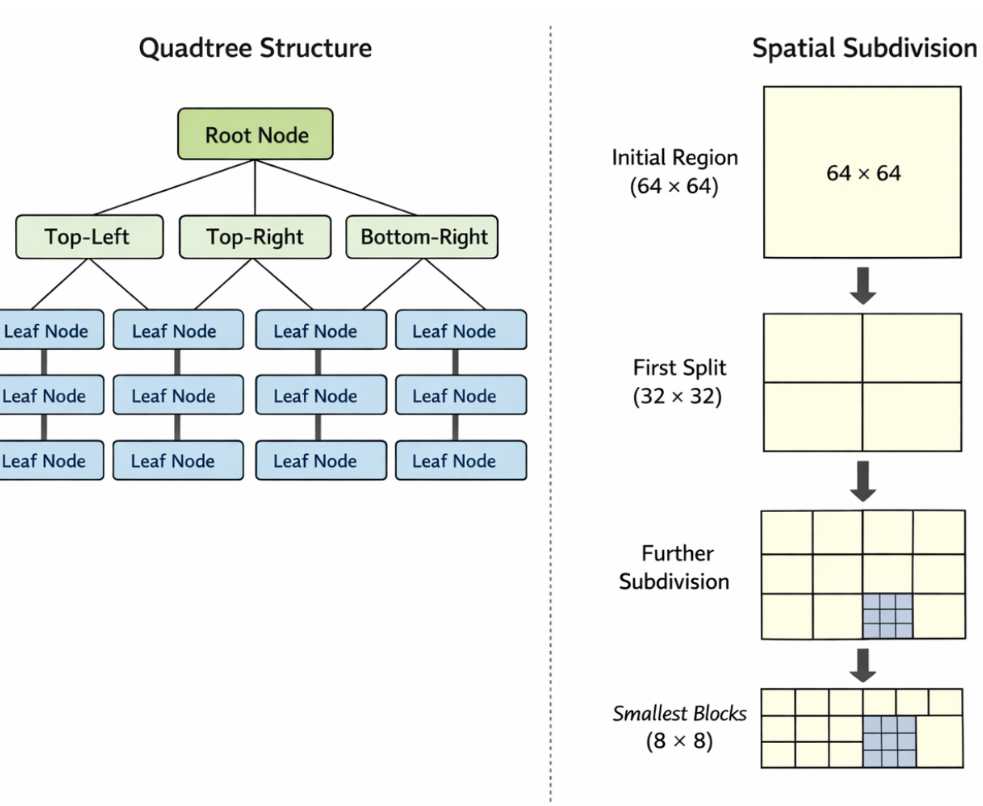
四叉树是一种树状数据结构,其每个内部节点恰好有四个子节点。它主要用于对二维空间进行递归细分。你可以将其类比为一维空间中的二叉树,或者是三维空间中的八叉树(Octree)。
核心原理
四叉树的基本思想是:如果一个区域内包含的数据量超过了预设的阈值(容量),就将该区域等分为四个象限,并将数据分配到相应的子象限中。
通常,这四个象限被命名为:
- NW (North-West):左上象限
- NE (North-East):右上象限
- SW (South-West):左下象限
- SE (South-East):右下象限
四叉树的类型包括:
- 点四叉树 (Point Quadtree):用于存储二维点坐标。
- 区域四叉树 (Region Quadtree):常用于图像处理,根据颜色一致性划分。
- 物体四叉树 (MX-CIF Quadtree):用于存储具有形状(如矩形、圆)的物体。
为什么要使用四叉树?
想象一个包含 10,000 个单位的游戏地图。如果你想检查哪些单位发生了碰撞,最直观的方法是两两比对。
- 朴素算法复杂度:O(n^2),即 10,000 * 10,000 = 100,000,000 次检查。
- 四叉树算法复杂度:通过将物体划分到不同的空间区域,你只需要检查同一区域内的物体。理想情况下,复杂度可降至 O(nlog n)。
示例(c++)
c++
#include <iostream>
#include <vector>
#include <memory>
#include <random>
#include <iomanip>
// --- 基础结构定义 ---
// 表示二维平面上的点
struct Point {
double x, y;
int id; // 增加 ID 方便辨认
};
// 轴对齐边界框 (Axis-Aligned Bounding Box)
struct AABB {
double x, y, w, h; // 中心点(x,y),半宽w,半高h
// 检查一个点是否在该范围内
bool contains(const Point& p) const {
return (p.x >= x - w && p.x <= x + w &&
p.y >= y - h && p.y <= y + h);
}
// 检查两个矩形是否相交
bool intersects(const AABB& other) const {
return !(other.x - other.w > x + w ||
other.x + other.w < x - w ||
other.y - other.h > y + h ||
other.y + other.h < y - h);
}
};
// --- 四叉树类定义 ---
class QuadTree {
private:
const int CAPACITY = 4; // 每个节点最多存放的点数
AABB boundary; // 节点的空间范围
std::vector<Point> points; // 当前节点存放的点
bool divided = false; // 是否已分裂
// 四个子节点:使用智能指针自动管理内存
std::unique_ptr<QuadTree> nw, ne, sw, se;
// 空间分裂
void subdivide() {
double x = boundary.x;
double y = boundary.y;
double w = boundary.w / 2.0;
double h = boundary.h / 2.0;
nw = std::make_unique<QuadTree>(AABB{x - w, y + h, w, h});
ne = std::make_unique<QuadTree>(AABB{x + w, y + h, w, h});
sw = std::make_unique<QuadTree>(AABB{x - w, y - h, w, h});
se = std::make_unique<QuadTree>(AABB{x + w, y - h, w, h});
divided = true;
}
public:
QuadTree(AABB boundary) : boundary(boundary) {}
// 插入点
bool insert(Point p) {
// 如果点不在当前范围内,返回失败
if (!boundary.contains(p)) return false;
// 如果未满且未分裂,存入当前节点
if (points.size() < CAPACITY && !divided) {
points.push_back(p);
return true;
}
// 超过容量,如果还没分裂则分裂
if (!divided) subdivide();
// 尝试递归插入子节点
if (nw->insert(p)) return true;
if (ne->insert(p)) return true;
if (sw->insert(p)) return true;
if (se->insert(p)) return true;
return false;
}
// 范围查询
void query(const AABB& range, std::vector<Point>& found) {
// 如果查询范围与当前节点无交集,直接返回
if (!boundary.intersects(range)) return;
// 检查当前节点的点
for (const auto& p : points) {
if (range.contains(p)) {
found.push_back(p);
}
}
// 如果已分裂,递归查询子节点
if (divided) {
nw->query(range, found);
ne->query(range, found);
sw->query(range, found);
se->query(range, found);
}
}
};
// --- 主函数:测试 ---
int main() {
// 1. 初始化四叉树:范围为 x[-200, 200], y[-200, 200]
AABB worldBoundary = {0, 0, 200, 200};
QuadTree qt(worldBoundary);
// 2. 随机生成 50 个点并插入
std::mt19937 rng(12345); // 固定种子以便复现
std::uniform_real_distribution<double> dist(-200.0, 200.0);
std::cout << "Inserting 50 points..." << std::endl;
for (int i = 0; i < 50; ++i) {
Point p = {dist(rng), dist(rng), i};
qt.insert(p);
}
// 3. 执行范围查询
// 查询中心在 (50, 50),宽高各为 100 的矩形区域 (w=50, h=50)
AABB searchRange = {50, 50, 50, 50};
std::vector<Point> results;
qt.query(searchRange, results);
// 4. 输出结果
std::cout << "\n--- Query Results ---" << std::endl;
std::cout << "Search Box: Center(50,50), Width 100, Height 100" << std::endl;
std::cout << "Found " << results.size() << " points:" << std::endl;
std::cout << "ID\tX\t\tY" << std::endl;
std::cout << "---------------------------------" << std::endl;
for (const auto& p : results) {
std::cout << p.id << "\t"
<< std::fixed << std::setprecision(2) << p.x << "\t\t"
<< p.y << std::endl;
}
return 0;
}关键操作:
- 插入 (Insertion)
当你向树中添加一个点时,首先检查该点是否属于当前节点的边界。
- 如果是,且当前节点未满,则直接存入。
- 如果已满,且尚未分裂,则调用
subdivide()将当前区域一分为四。 - 递归地尝试将该点存入四个子节点中。
- 细分 (Subdivision)
细分是四叉树动态生长的关键。它将父矩形切分为四个相等的小矩形。在 C++ 实现中,使用 std::unique_ptr 可以很好地管理内存,防止内存泄漏。
- 范围查询 (Range Query)
这是四叉树最有价值的地方。如果你想查找某个矩形范围内的所有物体,你不需要遍历整棵树:
- 如果查询范围与当前节点边界不相交,直接跳过该分支。
- 如果相交,检查当前节点的点,并递归搜索子节点。
性能分析与应用场景
- 空间复杂度:在最坏情况下(点非常密集),空间复杂度为 O(n * h),其中 h 是树深度。
- 时间复杂度 :
- 插入:平均 O(log n)。
- 查询:取决于分布,通常远优于 O(n)。
常见应用:
- 游戏引擎:用于检测数千个子弹与敌人之间的碰撞。
- 地图 API:如 Google Maps,根据缩放级别(LOD)加载不同精度的地图瓦片。
- 图像处理:一种有损压缩技术,对于颜色相近的整块区域只记录一个大节点,而非每个像素。
H265(HEVC)中的四叉树
CTU, CU, PU 与 TU
在 HEVC 中,四叉树的应用主要体现在两个层面:编码单位划分 和残差变换划分。
- CTU (Coding Tree Unit) :类似于 H.264 的宏块,但尺寸更大(通常为 64 * 64)。它是四叉树划分的根节点。
- CU (Coding Unit) :CTU 递归划分出的子叶节点。CU 是进行帧内/帧间预测模式选择的基本单位。
- PU (Prediction Unit):在 CU 级别决定预测模式后,CU 可以进一步划分成 PU 来执行具体的预测算法(对称或非对称划分)。
- TU (Transform Unit) :CU 内部用于离散余弦变换 (DCT) 和量化的基本单位,同样采用四叉树结构(称为 RQT, Residual Quadtree)。
四叉树划分的具体流程
HEVC 的四叉树划分是一个基于率失真优化 (RDO, Rate-Distortion Optimization) 的递归搜索过程。
第一步:确定 CTU 尺寸
编码器将一帧图像分成若干个固定大小的 CTU(如 64 * 64)。
第二步:递归拆分 CU (Coding Tree Split)
-
评估当前块:计算当前块(例如 64 * 64)在不拆分情况下的率失真代价 RDroot。
-
尝试拆分:将当前块等分为 4 个子块(每个 32 * 32)。
-
递归向下:对每个子块重复上述过程,直到达到最小允许的 CU 尺寸(如 8 * 8)。
-
回溯比较:
-
计算 4 个子块的最佳 RD 总和:
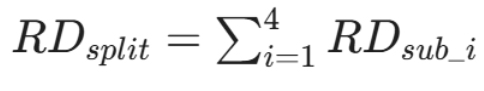
-
比较决策:如果 RDsplit < RDroot,则保留拆分;否则,将该块作为叶节点 CU,不再拆分。
-
第三步:确定预测单位 (PU)
当 CU 划分确定后,每个叶节点 CU 会决定如何进行预测。
- 帧内预测:CU 可以是对称的 2N * 2N 或 N * N。
- 帧间预测:支持对称划分(如 2N * 2N)和非对称划分(AMP,如 2N * nU),以便更精确地匹配运动物体的边界。
第四步:残差四叉树划分 (RQT / TU Split)
预测完成后,产生的残差数据需要进行变换。
- 残差块(通常与 CU 同大)作为残差四叉树的根。
- 根据残差的能量分布,再次通过四叉树决定是否拆分为更小的 TU(例如从 32 * 32 拆到 4 * 4)。
- 较小的 TU 能够更好地捕捉高频细节,而较大的 TU 在平坦区域能提供更高的能量集中度。
为什么四叉树在 HEVC 中如此有效?
| 特性 | 优势描述 |
|---|---|
| 内容自适应 | 平坦区域(如蓝天)使用大 CU,减少头信息开销;复杂区域(如人脸)使用小 CU,提高预测精度。 |
| 灵活的变换尺寸 | RQT 允许变换矩阵的大小与残差特性匹配,极大提升了变换效率。 |
| 信令压缩 | 编码器只需发送简单的"划分标志位(split_flag)",解码器即可重建整棵树。 |
总结
四叉树是平衡"空间精度"与"计算效率"的经典工具。在实际工程中,你可能还需要考虑以下优化:
- 动态删除:当物体移动时,需要从旧节点删除并重新插入新节点。
- 非均匀分布处理:如果所有点都在同一个位置,四叉树会深度退化。
- 松散四叉树 (Loose Quadtree):为了处理边界上的物体,增加节点边界的重叠量。