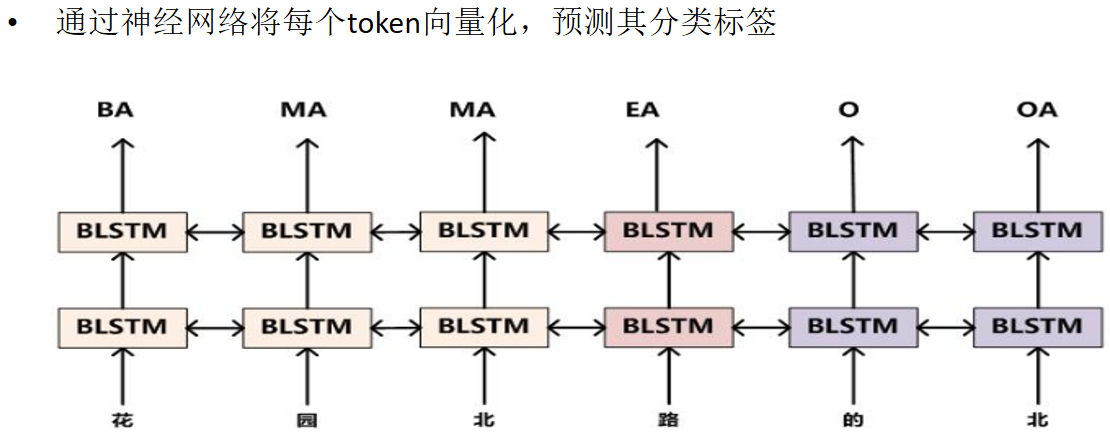
CRF 简介:定义与实例
1. 什么是 CRF
CRF(Conditional Random Field,条件随机场)是一种用于序列标注 的概率图模型。它能够同时考虑当前标签与相邻标签之间的依赖关系 ,在整个序列上寻找全局最优的标签序列,而不是逐位置独立地做分类决策。
在命名实体识别(NER)中,CRF 常作为分类器的后处理层,用来约束标签序列的合法性(如 BIO 标注体系中 I-XXX 不能无缘无故出现)。
1.1 序列任务(Sequence Labeling)定义
给定输入序列 x = ( x 1 , ... , x T ) x=(x_1,\dots,x_T) x=(x1,...,xT),模型需要为每个位置预测一个标签,输出序列 y = ( y 1 , ... , y T ) y=(y_1,\dots,y_T) y=(y1,...,yT)。常见任务包括分词、词性标注、命名实体识别等。它的关键特点是标签之间存在依赖关系,不仅要考虑当前输入,还要考虑前后标签的一致性。
2. CRF 的核心作用
CRF 的核心优势可以概括为三点:
- 建模标签转移 :学习标签之间的转移概率,例如
B-PERSON → I-PERSON应该更常见。 - 约束标签合法性 :避免出现不合法的标签序列(如
O → I-PERSON)。 - 全局最优解码:使用 Viterbi 算法在整个序列上找到最佳标签组合。
3. CRF-Loss(条件随机场损失)
假设输入序列为 x = ( x 1 , x 2 , ... , x T ) x=(x_1,x_2,\dots,x_T) x=(x1,x2,...,xT),标签序列为 y = ( y 1 , y 2 , ... , y T ) y=(y_1,y_2,\dots,y_T) y=(y1,y2,...,yT)。
CRF-Loss 的核心是最大化真实路径概率 ,等价于最小化负对数似然。
先定义整条序列的打分函数:
s ( x , y ) = ∑ t = 1 T ( A y t − 1 , y t + P t , y t ) s(x,y)=\sum_{t=1}^{T}\big(A_{y_{t-1},y_t}+P_{t,y_t}\big) s(x,y)=t=1∑T(Ayt−1,yt+Pt,yt)
其中:
- A i , j A_{i,j} Ai,j 是转移矩阵 (Transition Matrix)里的元素,表示从标签 i i i 转移到标签 j j j 的得分。
- 转移矩阵 A A A 的 shape 为
label_num × label_num(即 m × m m \times m m×m,其中 m m m 为标签总数) - 物理意义:行对应"前一个标签",列对应"后一个标签",数值越高表示该标签转移越合理(如 A B-LOCATION , I-LOCATION A_{\text{B-LOCATION},\text{I-LOCATION}} AB-LOCATION,I-LOCATION 得分高, A O , I-LOCATION A_{\text{O},\text{I-LOCATION}} AO,I-LOCATION 得分低)
- 数值来源:CRF 自身的可学习参数,训练中通过梯度下降优化,初始为随机值(如正态分布)
- 示例(标签集:O、B-LOCATION、I-LOCATION):
- 转移矩阵 A A A 的 shape 为
| 前标签\后标签 | O | B-LOCATION | I-LOCATION |
|---|---|---|---|
| O | 3.5 | 2.0 | -1.0 |
| B-LOCATION | -0.5 | -1.0 | 4.0 |
| I-LOCATION | 1.5 | -0.8 | 3.0 |
- P t , y t P_{t,y_t} Pt,yt 是发射得分 (Emission Score),表示在位置 t t t 选择标签 y t y_t yt 的得分(通常来自上游模型的 logits)。
- 发射矩阵 P P P 的 shape 为
seq_length × label_num(即 T × m T \times m T×m,其中 T T T 为序列长度, m m m 为标签总数) - 物理意义:每一行对应序列中一个位置,每一列对应一个标签,数值越高表示该位置属于对应标签的可能性越大
- 数值来源:上游模型(如 LSTM/Transformer)的输出,并非 CRF 学习的参数,随上游模型训练更新
- 示例(序列:"我 在 北 京 工 作",标签集:O、B-LOCATION、I-LOCATION):
- 发射矩阵 P P P 的 shape 为
| 位置 | O | B-LOCATION | I-LOCATION |
|---|---|---|---|
| 我 | 2.5 | 0.1 | 0.05 |
| 在 | 3.0 | 0.2 | 0.1 |
| 北 | 0.3 | 4.8 | 0.5 |
| 京 | 0.2 | 0.4 | 5.0 |
| 工 | 2.8 | 0.15 | 0.08 |
| 作 | 2.9 | 0.12 | 0.06 |
CRF 的条件概率为:
p ( y ∣ x ) = exp ( s ( x , y ) ) ∑ y ′ exp ( s ( x , y ′ ) ) p(y|x)=\frac{\exp(s(x,y))}{\sum_{y'}\exp(s(x,y'))} p(y∣x)=∑y′exp(s(x,y′))exp(s(x,y))
训练时最小化负对数似然(NLL),这就是 CRF-Loss:
L = − log p ( y ∣ x ) \mathcal{L}=-\log p(y|x) L=−logp(y∣x)
等价地可以写成:对数似然 = 真实路径分数 − log ∑ y ′ exp ( s ( x , y ′ ) ) \log \sum_{y'}\exp(s(x,y')) log∑y′exp(s(x,y′)),因此损失就是两者的相反数。
预测时使用 Viterbi(维特比算法) 算法求:
y ∗ = arg max y s ( x , y ) y^*=\arg\max_y s(x,y) y∗=argymaxs(x,y)
为了真正"可应用",你需要知道 CRF 的训练和解码具体在做什么:
训练的关键在于计算两项:
- 真实路径的分数 s ( x , y ) s(x,y) s(x,y)(上面已给出)
- 所有路径的归一化项 log ∑ y ′ exp ( s ( x , y ′ ) ) \log \sum_{y'}\exp(s(x,y')) log∑y′exp(s(x,y′))
这一项可以用 前向算法(Forward Algorithm) 在 O ( T ⋅ m 2 ) O(T\cdot m^2) O(T⋅m2) 时间内计算,其中 m m m 为标签数。
实际实现中,CRF 的 loss 就是:
L = log ∑ y ′ exp ( s ( x , y ′ ) ) − s ( x , y ) \mathcal{L}=\log \sum_{y'}\exp(s(x,y'))-s(x,y) L=logy′∑exp(s(x,y′))−s(x,y)
这表示:让正确路径分数尽可能高,同时压低错误路径的总分。
4. 转移矩阵的直观含义
转移矩阵 A A A 的大小为 m × m m \times m m×m( m m m 为标签数),shape 为 label_num × label_num。
每个元素 A i , j A_{i,j} Ai,j 代表标签从 i i i 到 j j j 的转移得分,例如:
- A B-LOCATION , I-LOCATION A_{\text{B-LOCATION},\text{I-LOCATION}} AB-LOCATION,I-LOCATION 应该较高
- A O , I-LOCATION A_{\text{O},\text{I-LOCATION}} AO,I-LOCATION 应该较低(不合法转移)
可以理解为一张"规则表",让模型更偏向合法的标签序列。
5. 维特比解码(Viterbi Decoding)
CRF 的预测目标是找到最大路径分数:
y ∗ = arg max y s ( x , y ) y^*=\arg\max_y s(x,y) y∗=argymaxs(x,y)
直接枚举所有标签序列会是 m T m^T mT 级别,无法接受。
维特比算法用动态规划把复杂度降到 O ( T ⋅ m 2 ) O(T\cdot m^2) O(T⋅m2):
定义递推:
δ t ( j ) = max i ( δ t − 1 ( i ) + A i , j ) + P t , j \delta_t(j)=\max_i\big(\delta_{t-1}(i)+A_{i,j}\big)+P_{t,j} δt(j)=imax(δt−1(i)+Ai,j)+Pt,j
含义:位置 t t t 选择标签 j j j 的最佳路径分数 。
然后通过回溯指针找出整条最优路径。
6. Beam Search(束搜索)与 CRF
Beam Search 是一种近似搜索策略:
每个时间步只保留分数最高的 k k k 条部分路径(beam size = k k k), 从而把搜索复杂度从指数级降到 O ( T ⋅ k ⋅ m ) O(T\cdot k\cdot m) O(T⋅k⋅m)。
在 CRF 中,标准解码用的是维特比(精确最优)。
但在以下场景可能会用 Beam Search:
- 标签空间很大( m m m 很大), m 2 m^2 m2 过慢
- 需要输出多个候选序列(Top-k)
- 与其他解码约束结合时,维特比难以直接应用
注意:Beam Search 是近似的,不保证全局最优,但速度更快。
7. 实际例子讲解
假设句子是:
"我 在 北 京 工 作"
我们用 BIO 标注体系:
正确标签应为:
O O B-LOCATION I-LOCATION O O
7.1 不使用 CRF 的情况(逐位置独立分类)
假设模型逐位置输出的标签概率最高的结果是:
O O B-LOCATION O O O
这种预测在局部看似合理,但会导致实体"北京"只预测了一个字"北",实体边界被截断。
另一个可能的错误是:
O O I-LOCATION I-LOCATION O O
这会产生 非法序列 ,因为 I-LOCATION 不能直接出现在 O 后面。
7.2 使用 CRF 的情况(考虑全局转移)
CRF 会学习一个标签转移矩阵,例如:
B-LOCATION → I-LOCATION 具有高分
O → I-LOCATION 具有低分(甚至被惩罚)
因此在解码时,CRF 会优先选择全局最合理的序列:
O O B-LOCATION I-LOCATION O O
这样实体"北京"就会被完整正确地识别出来。
8. 小结
CRF 不会改变模型对单个位置的分类能力,但它通过学习标签之间的转移关系,使最终输出的标签序列更符合实际规则。对于 NER 等序列标注任务,CRF 常常能带来更稳定、更合理的识别结果。