目录
[1 插值](#1 插值)
[1.1 一维插值](#1.1 一维插值)
[1.2 多维插值](#1.2 多维插值)
[1.3 多输出插值](#1.3 多输出插值)
[2《WeatherBench: A benchmark data set for data-driven weather forecasting》论文阅读](#2《WeatherBench: A benchmark data set for data-driven weather forecasting》论文阅读)
[2.1 背景](#2.1 背景)
[2.2 方法论](#2.2 方法论)
[2.3 创新点](#2.3 创新点)
[2.4 实验结果](#2.4 实验结果)
[3 总结](#3 总结)
摘要
本周首先学习了上周接触到的插值方法,了解了它的定义、方法以及对应的优缺点与应用场景,具体包括线性插值、多项式插值与反距离加权等;其次阅读了《WeatherBench: A benchmark data set for data-driven weather forecasting》这篇论文,了解了它的背景、方法论与创新点等。
Abstract
This week, I first studied the interpolation methods introduced last week, examining its definition, methods, as well as their corresponding advantages, disadvantages, and application scenarios, specifically including linear interpolation, polynomial interpolation, and inverse distance weighting. Subsequently, I read the paper titled "WeatherBench: A benchmark data set for data-driven weather forecasting," gaining an understanding of its background, methodology, and innovations.
1 插值
插值是一种通过已知的离散数据点来构造一个函数(曲线或曲面),使其恰好通过所有已知数据点,并据此估算未知点函数值的方法。这个函数就被叫做插值函数,它必须经过所有给定的样本点,且主要用于估算已知数据点之间的值,已知数据点之外需谨慎使用。
这个概念很容易与拟合相互混淆。它们的区别在于插值函数的曲线必须经过过所有数据点,强调精确性;而拟合的曲线不要求经过所有点,而是寻找一个最佳趋势,以最小化整体误差。
1.1 一维插值
一维插值只有一个自变量,一个因变量,函数形式通常为 y=f(x) ,它的几何表现是平面上的一条曲线。常见的一维插值方法包括最近邻插值、线性插值、多项式插值与分段多项式插值。
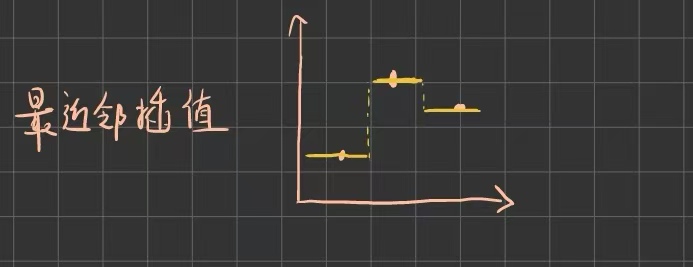
最近邻插值的思想是,对于待求的未知点,其值与离它最近的已知点的值相等。这种方法能够保持原始值,实现简单,计算速度也很快,因为它只需要进行四舍五入和内存拷贝操作,没有复杂的乘除运算,在所有插值方法中复杂度最低(O(1))。但它只依赖于最近的一个点,忽略其他邻近点的信息,会产生不连续的阶梯状结果,质量比较低下。也因此,最近邻插值比较适用于像素艺术和复古游戏图形的放大、实时性要求极高或者更复杂算法的初步处理,还有分类数据或标签数据的重采样等场景。
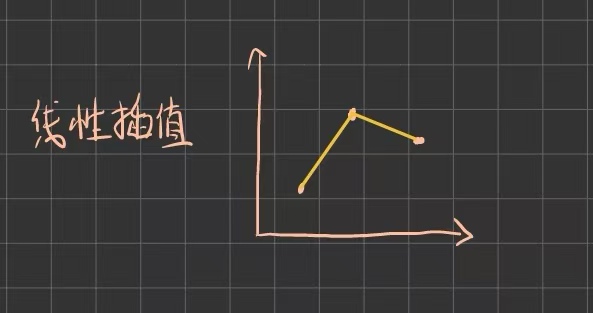
线性插值的思想也比较简单,即在两个已知点之间用直线连接,再根据待插值点在直线上的位置按比例计算其值。它的计算过程是,先计算 x 相对区间 的位置:
然后,计算插值结果:
这个计算插值结果的公式也叫 lerp 公式。
它的优点是简单、快速,因为只涉及基本的加减乘除,没有复杂运算,但由于其整体是分段折线,所以在数据点处虽然连续,但不可导,不够平滑,且精度有限。故线性插值主要适用于数据初步估算、可视化等场景。
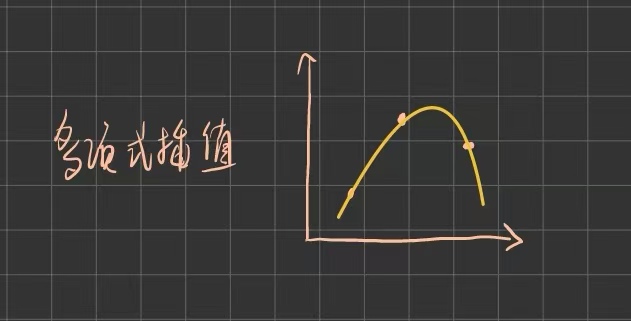
多项式插值的思想是直接构造一个通过所有数据点的 n 次多项式,比如三次插值就是用的三次多项式。
在数学上,它的具体描述是:给定 n+1 个 互不相同的数据点
,找到一个次数不超过 n 的多项式
使得
,构造方法则包括拉格朗日插值法和牛顿插值法,它们给出的是同一个多项式,满足相同的插值条件,只是表达形式不同。多项式插值形式简洁且理论完整,但数据点多(高次)时计算量大,还会出现龙格现象使误差在边缘急剧增大,对区间外的外推也非常不可靠。也因此,这种方法比较适合数据点较少的情况,通常用于理论分析、符号计算等场景。
p.s. 龙格现象是指对某些函数使用等距节点进行高次多项式插值时,在区间端点附近会出现剧烈的振荡。
分段多项式插值主要用于解决高次多项式问题,它为了克服单一高次多项式的缺点,会将整个区间分成多个小段,在每段上用低次多项式进行插值,主要包括分段线性插值与三次样条插值等等。
分段线性插值就是每段上用线性插值,整体是连续但不可导的折线;
三次样条插值是最常用、最重要的插值方法之一,它的思想是在每个子区间上使用一个三次多项式,并强制满足函数通过所有数据点、边界条件以及在数据点处,一阶导数和二阶导数连续三个条件。它具有非常好的光滑性,没有龙格现象,视觉效果和物理意义都很优良,适用于计算机图形学(曲线设计)、CAD、地理信息系统、动画路径规划等多种场景。
1.2 多维插值
多维插值有多个自变量,函数形式类似于 z=f(x,y) (以二维插值为例),几何表现可能是一个曲面或者一个标量场。
其中二维插值主要包括双线性插值与双三次插值。双线性插值是前面线性插值的扩展,它会先在 x 方向线性插值两次,再在 y 方向线性插值一次,常用于图像缩放、地形网格等场景;而双三次插值相较而言会使用更多的周边点,能提供更平滑、边缘保持更好的结果,是高质量图像缩放的核心算法。
当数据点不规则分布时(如气象站、测量点),上述基于网格的方法不再适用,散乱数据插值就会发挥作用,它主要包括反距离加权法、径向基函数插值与克里金法。
反距离加权法中,未知点的值是周围已知点的加权平均,权重与距离的某次方成反比。这种方法简单直观,且能够精确通过数据点,但容易产生"牛眼"效应,不支持外推,还需要选择幂参数和搜索半径。
p.s. "牛眼"效应在插值结果的可视化图上表现为围绕每个已知数据点的一系列闭合的、圆形的等值线,但自然现象(如温度、降雨)的分布很少是完美的圆形,会误导观察者对空间格局的理解,不符合物理现实,会降低地图的可信度。
径向基函数插值则是使用一个仅与距离有关的函数(如高斯函数)作为基函数进行拟合。它是当前最主流、最强大的散乱数据插值方法之一,可以处理任意维度、任意分布的数据,能生成光滑曲面,但需要选择基函数和形状参数,计算复杂度也很高。这种方法主要应用于地形建模、气象数据同化、机器学习(RBF网络)、3D重建等领域。
克里金法将数据视为随机场的实现,不仅考虑距离,还考虑空间上的相关性,是一种高级的地质统计学方法。这种方法在考虑空间结构的同时能够提供不确定性估计,但需要的数据量较大、计算成本也很高。它主要应用在矿产储量估计、环境监测、土壤科学、气象预报等场景。
1.3 多输出插值
前面讨论的都是单一输出的情况,多输出也有对应的插值方法,即多输出插值,也称向量值插值,它只有一个自变量,却有多个因变量,函数形式为 (x,y) = f(t) ,几何表现为一条曲线,但这条曲线位于高维的输出空间中。
多输出插值主要有两种实现策略。一种是分量独立插值,即对每个输出分量分别进行单输出插值,实现简单且能为不同分量选择不同插值方法,但可能破坏输出变量间的内在关系,导致几何上不理想的结果,也不保证结果满足某些跨分量的约束条件;另一种是整体向量插值,即直接构造向量值插值函数,可以方便地加入跨分量约束,保持分量的相关性,更符合某些物理问题的本质。
第一种跟神经网络的多分类输出处理异曲同工。在前面学习神经网络的分类问题时,如果需要解决多类别分类问题,就可以建立一个有多个输出单元的神经网络,其输出将会是一个多维向量,每个单元用于判断一个类别。假设有四个类别(对应单元从上到下)分别为家人、朋友、伴侣、同事,当输入属于家人时,理想的输出为:
实际上就是四个二维分类,即判断是否为家人、朋友、伴侣和同事,对应上面的"对每个输出分量分别进行单输出插值"。
2《WeatherBench: A benchmark data set for data-driven weather forecasting》论文阅读
论文链接:[2002.00469] WeatherBench: A benchmark dataset for data-driven weather forecasting
2.1 背景
深度学习作为机器学习的一个分支,主要由数据驱动,可用于许多任务,尤其是图像识别和自然语言处理,而传统的天气预测(NWP)主要基于物理方程在超级计算机上求解,虽然准确,但存在计算成本高昂、分辨率受限以及物理参数化不确定等显著限制。因此,人们想要通过数据驱动的方式来加速与改进 NWP。
而近年来,数据驱动的天气预报方法也显示出巨大的潜力,它们可以直接从数据中学习复杂的非线性关系,推理速度也很快。然而,该领域早期研究使用不同数据、评估指标和验证期,标准化的基准数据集和评估指标匮乏,这导致不同研究的结果难以直接比较,且研究进展碎片化,阻碍了领域发展。
2.2 方法论
WeatherBench 的核心是构建一个统一的数据集和评估框架,主要包括数据标准化、任务定义与基线模型设计三个部分。
**数据标准化:**它的数据源是 1979~2018 年的 ERA5 再分析数据,包括低中高三个分辨率选项,经过重网格化、归一化、数据分割以及变量选择等预处理步骤,最终输出为 NetCDF 格式,并提供了用于数据加载的代码。
p.s. ERA5是欧洲中期天气预报中心的全球再分析数据,可通过Copernicus CDS免费下载。
**任务定义:**论文明确定义了三个基准任务,分别是确定性天气预报、概率预报与极端事件预测。其中确定性天气预报根据当前时刻的 3D 大气状态预测未来 3-5 天的天气场,并通过均方根误差、异常相关系数与连续分级概率评分等评估指标进行评估;概率预报使用集合方法量化不确定性;极端事件预测则更加关注热带气旋路径、极端降水等。
基线模型设计:论文提供了五个层级的基线,包括假设天气不变的持久性预报、使用多年同日的平均值的气候学预报、使用简单平流方程的物理基线、传统机器学习(如随机森林),还有深度学习基线(如 CNN、U-Net 等)
2.3 创新点
WeatherBench 的创新点主要包括:
**标准化基准:**首次为数据驱动的天气预报提供了统一的、标准化的数据集、评估指标和基线模型,使得不同研究之间的比较成为可能。
**全面的基线与评估指标:**不仅提供了简单的统计模型,还提供了经典的数值天气预报结果和深度学习基线,设定了性能门槛。同时结合传统机器学习指标和气象领域专用指标以确保评估的科学性。
**可扩展性:**数据集设计考虑了不同分辨率,适合不同复杂度的模型。同时,提供了便捷的数据加载和评估工具,降低了入门门槛。
2.4 实验结果
论文中比较了多种基线模型在不同变量、不同预报时长下的表现。主要结论包括:
首先,简单的深度学习模型(如CNN)在短期预报(1-3天)上可以接近甚至超越物理模型(如持久化预测和气候学平均),但随预报时效延长,优势减小,且在极端天气事件上仍存在一定差距。
其次,深度学习需要大量数据,但达到基准性能后,增加数据收益递减。同时随着分辨率的提高,深度学习模型的性能有所提升,但计算成本也相应增加。
然后,不同气象变量的预测难度不同,例如,温度预测相对容易,而降水预测更具挑战性。
这些结果为后续研究提供了重要的参考,指明了改进方向。
3 总结
本周对于上周了解到的插值方法进行了学习,感觉多维插值中径向基函数与克里金两种方法后续还可以更深入地学习下。同时阅读了一篇气象与深度学习交叉的论文用于入门,总体读得比较粗略,论文整体差不多是对前面气象与深度学习两个领域的研究进行了一些整合与标准化,并放到对应的平台上,方便后人研究使用,下周可以尝试实践使用一下这个平台。