计算2的N次方和大整数的因子

计算2的N次方

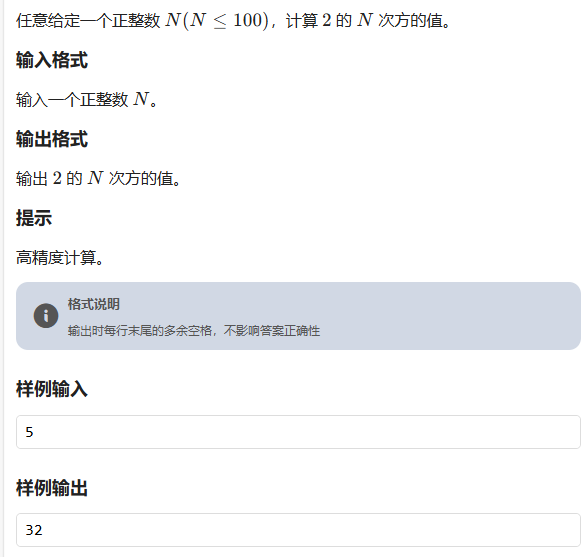
用数组存储大整数，每一位存储一个数字（0-9），然后进行 N 次乘以 2 的操作。

cpp 复制代码

#include <bits/stdc++.h>
using namespace std;

int main() {
    int N;
    cin >> N;
    
    // 2^0 = 1，初始值
    int num[100] = {1};  // 存储结果的每一位（逆序存储，个位在num[0]）
    int len = 1;         // 当前数字的长度
    
    // 进行 N 次乘以 2 的操作
    for (int i = 0; i < N; i++) {
        int carry = 0;  // 进位
        
        // 每一位都乘以 2
        for (int j = 0; j < len; j++) {
            int product = num[j] * 2 + carry;
            num[j] = product % 10;  // 当前位的值
            carry = product / 10;   // 进位
        }
        
        // 处理最后的进位
        while (carry > 0) {
            num[len] = carry % 10;
            carry /= 10;
            len++;
        }
    }
    
    // 输出结果（逆序输出）
    for (int i = len - 1; i >= 0; i--) {
        cout << num[i];
    }
    cout << endl;
    
    return 0;
}

大整数的因子

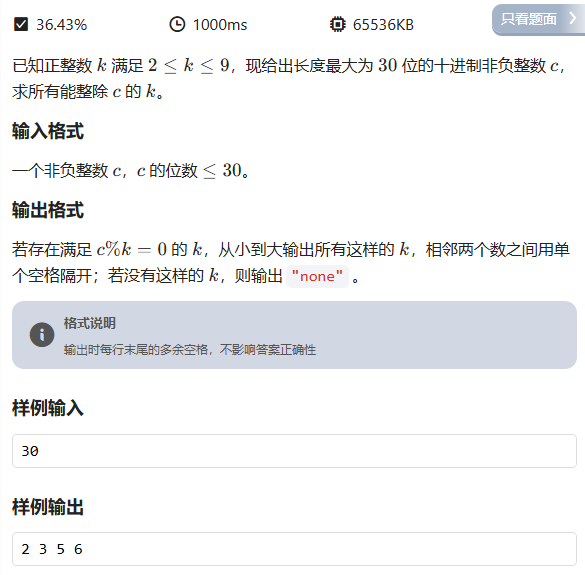
这个问题需要判断一个大整数（最多30位）能否被 2-9 中的某个数整除。因为 c 可能很大，我们需要用字符串读取这个数，然后分别判断整除性。

由于 c 最多有 30 位，无法用普通整数类型存储，所以：

将 c 作为字符串读入
对每个 k (2 ≤ k ≤ 9)，判断 c 是否能被 k 整除
使用大整数除法取余的方法来判断整除性

cpp 复制代码

#include <bits/stdc++.h>
using namespace std;

int main() {
    string c;
    cin >> c;
    
    bool found = false;  // 是否找到符合条件的 k
    
    // 检查 k 从 2 到 9
    for (int k = 2; k <= 9; k++) {
        int remainder = 0;
        
        // 模拟大整数除以 k 的过程
        for (char digit : c) {
            int num = digit - '0';
            remainder = (remainder * 10 + num) % k;
        }
        
        // 如果余数为 0，说明能整除
        if (remainder == 0) {
            if (found) {
                cout << " ";  // 不是第一个数，输出空格
            }
            cout << k;
            found = true;
        }
    }
    
    if (!found) {
        cout << "none";
    }
    cout << endl;
    
    return 0;
}

计算2的N次方 和 大整数的因子

计算2的N次方和大整数的因子