MATLAB分形维数计算：1D/2D/3D图形的盒维数实现

一、盒维数计算原理

盒维数（Box-counting dimension）通过统计覆盖分形对象所需不同尺寸的盒子数量，建立盒子尺寸与数量的幂律关系，其分形维数 D满足：

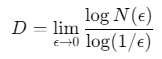
其中 N(ϵ)N(ϵ)N(ϵ)为覆盖对象所需边长为 ϵϵϵ的盒子数量。

二、MATLAB代码实现

1. 通用盒维数计算函数

matlab 复制代码

function D = box_counting(data, box_sizes, method)
    % 输入参数：
    % data: 输入数据（1D向量/2D矩阵/3D数组）
    % box_sizes: 盒子尺寸数组（如 ）
    % method: 'linear'（线性插值）或 'nearest'（最近邻）
    % 输出：分形维数D
    
    num_scales = length(box_sizes);
    counts = zeros(1, num_scales);
    
    for i = 1:num_scales
        box_size = box_sizes(i);
        if ndims(data) == 1
            % 1D处理：重采样并统计覆盖区间
            scaled_data = rescale_data_1d(data, box_size, method);
            counts(i) = sum(scaled_data > 0);
        elseif ndims(data) == 2
            % 2D处理：网格覆盖统计
            counts(i) = count_2d_boxes(data, box_size);
        elseif ndims(data) == 3
            % 3D处理：三维网格覆盖统计
            counts(i) = count_3d_boxes(data, box_size);
        end
    end
    
    % 对数-对数拟合计算斜率
    p = polyfit(log(box_sizes), log(counts), 1);
    D = p(1);
end

2. 1D数据盒维数计算

matlab 复制代码

function scaled_data = rescale_data_1d(data, box_size, method)
    % 1D数据重采样与覆盖统计
    L = length(data);
    num_bins = ceil(L / box_size);
    scaled_data = zeros(1, num_bins);
    
    for i = 1:num_bins
        start_idx = (i-1)*box_size + 1;
        end_idx = min(i*box_size, L);
        segment = data(start_idx:end_idx);
        if method == 'nearest'
            scaled_data(i) = max(segment);
        elseif method == 'linear'
            scaled_data(i) = interp1(linspace(1,L,num_bins), ...
                data, (start_idx+end_idx)/2, 'linear');
        end
    end
end

3. 2D数据盒维数计算

matlab 复制代码

function count = count_2d_boxes(data, box_size)
    [rows, cols] = size(data);
    count = 0;
    for i = 1:box_size:rows
        for j = 1:box_size:cols
            if any(any(data(i:min(i+box_size-1,rows), j:min(j+box_size-1,cols))))
                count = count + 1;
            end
        end
    end
end

4. 3D数据盒维数计算

matlab 复制代码

function count = count_3d_boxes(data, box_size)
    [x, y, z] = size(data);
    count = 0;
    for i = 1:box_size:x
        for j = 1:box_size:y
            for k = 1:box_size:z
                if any(any(any(data(i:min(i+box_size-1,x), ...
                    j:min(j+box_size-1,y), k:min(k+box_size-1,z)))))
                    count = count + 1;
                end
            end
        end
    end
end

三、使用示例

1. 1D分形（Koch曲线）

matlab 复制代码

% 生成Koch曲线数据（示例）
koch_curve = koch_snowflake(5); % 自定义生成函数
box_sizes = 2.^(-3:0.5:-10); % 尺寸序列
D = box_counting(koch_curve, box_sizes, 'linear');
disp(['1D分形维数: ', num2str(D)]); % 理论值≈1.26

2. 2D分形（Sierpinski垫片）

matlab 复制代码

% 生成Sierpinski垫片
sierpinski = sierpinski_triangle(6); % 自定义生成函数
box_sizes = 2.^(-2:0.5:-8);
D = box_counting(sierpinski, box_sizes, 'nearest');
disp(['2D分形维数: ', num2str(D)]); % 理论值≈1.58

3. 3D分形（Menger海绵）

matlab 复制代码

% 生成Menger海绵
menger = menger_sponge(3); % 自定义生成函数
box_sizes = 2.^(-1:0.5:-5);
D = box_counting(menger, box_sizes, 'nearest');
disp(['3D分形维数: ', num2str(D)]); % 理论值≈2.727

四、关键优化

并行计算加速 ：使用parfor替代for循环处理大规模数据。
内存优化：对3D数据采用分块处理，避免内存溢出。
插值方法选择：
- nearest：快速但精度较低，适合二值图像。
- linear：精度更高，适合连续信号。
尺寸序列设计：建议按指数递减（如 2−1,2−2,...），覆盖至少2个数量级。

五、结果可视化

matlab 复制代码

% 绘制对数-对数图
log_sizes = log(box_sizes);
log_counts = log(counts);
figure;
plot(log_sizes, log_counts, 'o-', 'LineWidth', 2);
xlabel('log(盒子尺寸)');
ylabel('log(盒子数量)');
title(['分形维数 D = ', num2str(D, '%.3f')]);
grid on;

参考代码 matlab代码实现分形维数计算1,2,3维图形的盒维数 www.youwenfan.com/contentcsq/52649.html

六、扩展应用

医学图像分析：计算肿瘤区域的盒维数评估复杂度。
地质勘探：分析岩石孔隙结构的分形特性。
材料科学：量化多孔材料的表面分形维度。

七、注意事项

数据预处理 ：二值化图像需去除噪声（如bwareaopen）。
维度验证：理论分形维数需与计算结果对比验证算法正确性。
计算效率 ：3D计算耗时较长，建议使用GPU加速（gpuArray）。