神经网络就像搭积木,最基本的 "积木" 是神经元,把神经元分层连起来,就构成了能干活的网络。
1. 神经网络的基本结构
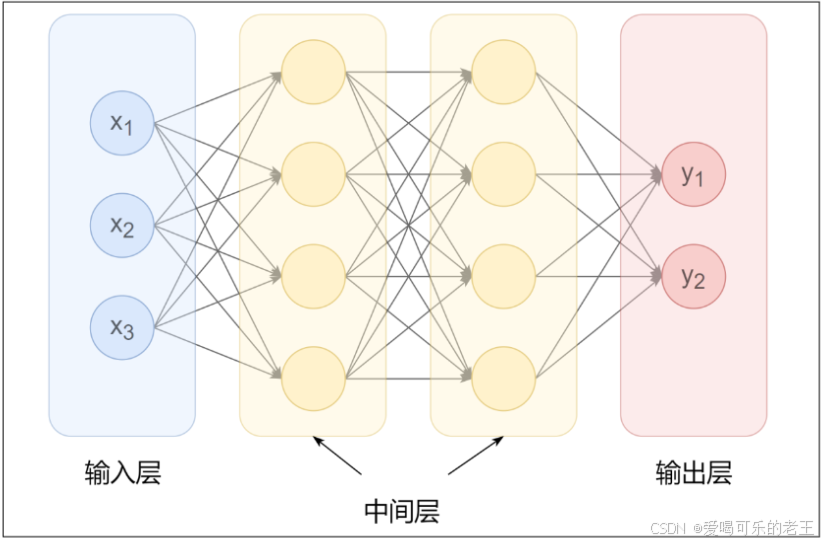
- 输入层:最左边一层,接收原始数据,比如图片的像素、文本的编码。
- 隐藏层:中间的所有层,是 "学习核心",层数越多,能学的规律越复杂。
- 输出层:最右边一层,输出结果,比如 "这是猫""这句话是正面评价"。
相邻层的神经元是全连接的,每个连接都有一个 "权重"(相当于信号的重要程度),信息从输入层一层层传到输出层,这个过程叫 "前向传播"。
2. 关键部件:激活函数(让网络 "会思考")
如果没有激活函数,神经网络就是简单的线性计算,再多层也没用。激活函数的作用是给网络引入 "非线性",让它能学懂复杂规律,常用的就 3 种,好记又好用:
2.1、阶跃(Binary step)函数
之前的感知机中,就是最简单的激活函数,它可以为输入设置一个"阈值";一旦超过这个阈值,就切换输出(0或者1)。这种函数被称为"阶跃函数"。
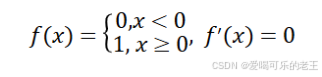
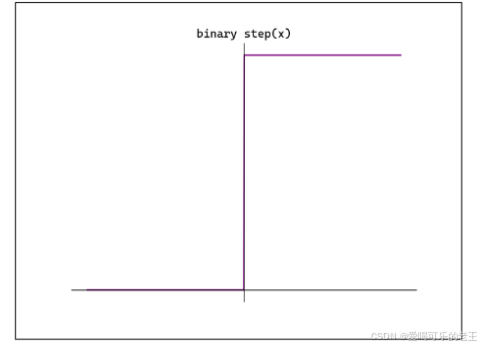
阶跃函数导数恒为0。可以用代码实现如下:
def step_function(x):
if x > 0:
return 1
else:
return 0这里的x只能取一个数值(浮点数)。如果我们希望直接传入Numpy 数组进行批量化的操作,可以改进如下:
def step_function(x):
return np.array(x > 0, dtype=int)2.2、Sigmoid函数
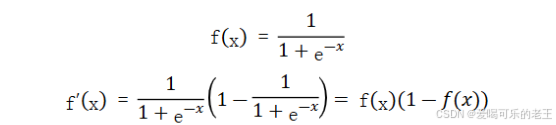
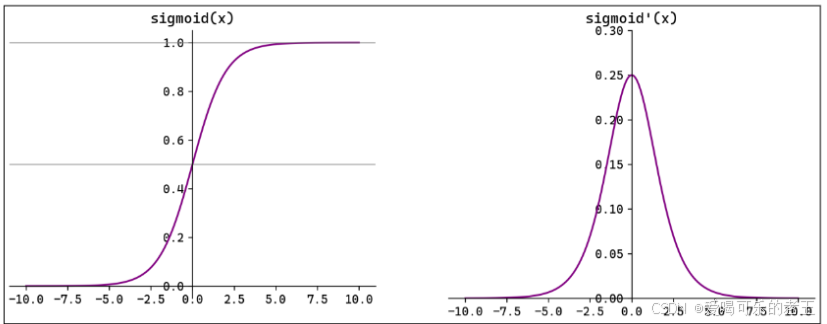
- Sigmoid(也叫Logistic 函数)是平滑的、可微的,能将任意输入映射到区间(0,1)。常用于二分类的输出层。但因其涉及指数运算,计算量相对较高。
- Sigmoid 的输入在[-6,6]之外时,其输出值变化很小,可能导致信息丢失。
- Sigmoid 的输出并非以0为中心,其输出值均>0,导致后续层的输入始终为正,可能影响后续梯度更新方向。
- Sigmoid 的导数范围为(0,0.25),梯度较小。当输入在[-6,6]之外时,导数接近 0,此时网络参数的更新将会极其缓慢。使用 Sigmoid作为激活函数,可能出现梯度消失(在逐层反向传播时,梯度会呈指数级哀减)。
Sigmoid 函数可以用代码实现如下:
def sigmoid(x):
return 1 / (1 + np.exp(-x))2.3、Tanh函数
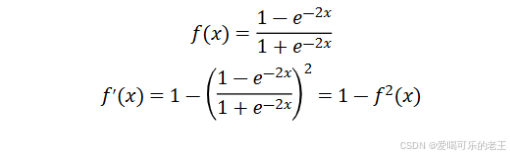
-
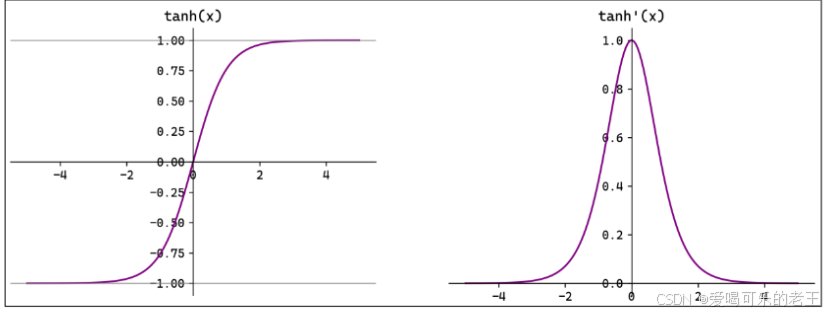
Tamh(双曲正切)将输入映射到区间(-1,1)。其关于原点中心对称。常用在隐藏层。
-
输入在[-3,3]之外时,Tanh 的输出值变化很小,此时其导数接近 0。
-
Tanh 的输出以0为中心,且其梯度相较于 Sigmoid 更大,收敛速度相对更快。但同样也存在梯度消失现象。
#直接调用numpy即可
np.tanh(x)
2.4、ReLU函数
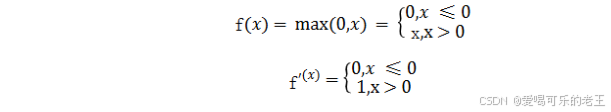
注意:x=O 时 ReLU 函数不可导,此时我们默认使用左侧的函数。
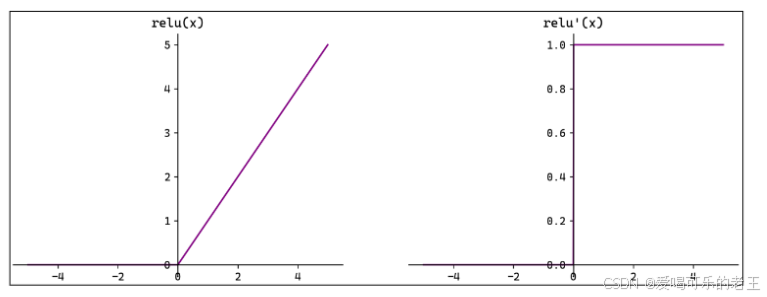
- ReLU(Rectified Linear Unit,修正线性单元)会将小于0的输入转换为0,大于等于0的输入则保持不变。ReLU定义简单,计算量小。常用于隐藏层。
- ReLU 作为激活函数不存在梯度消失。当输入小于 0时,ReLU 的输出为0,这意味着在神经网络中,ReLU激活的节点只有部分是"活跃"的,这种稀疏性有助于减少计算量和提高模型的效率。
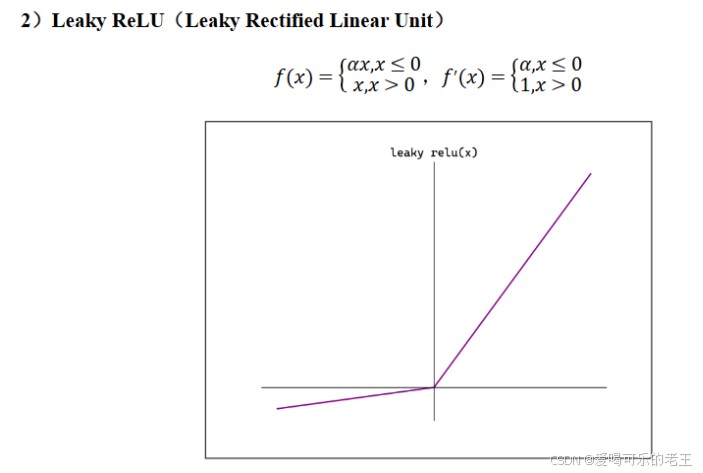
当神经元的输入持续为负数时,ReLU的输出始终为0。这意味着神经元可能永远不会被激活,从而导致"神经元死亡"问题。这会影响模型的学习能力,特别是如果大量的神经元都变成了"死神元".为解决此问题,可使用Leaky ReLU,其中α 是一个很小的常数)在负数区域引入一个小的斜率来解决"神经元死亡"问题。
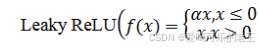
ReLU 函数可以用代码实现如下:
def relu(x):
return np.maximum(0, x)2.5、Softmax函数
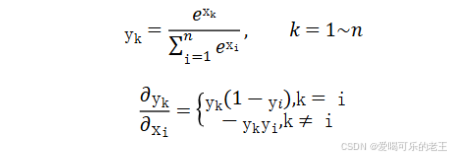
Softmax将一个任意的实数向量转换为一个概率分布,确保输出值的总和为1,是二分类激活函数 Sigmoid在多分类上的推广。Softmax常用于多分类问题的输出层,用来表示类别的预测概率。
Softmax会放大输入中较大的值,使得最大输入值对应的输出概率较大,其他较小的值会被压缩。即在类别之间起到了一定的区分作用。

Softmax函数可以用代码实现如下:
def softmax(x):
return np.exp(x) / np.sum(np.exp(x))
#考虑到x较大时,指数函数的值会非常大,容易溢出,可以改进为:
def softmax(x):
× = ×- np.max(x)# 溢出对策
return np.exp(x) / np.sum(np.exp(x))考虑到x为二维数组(矩阵)的情况,可以进一步写为:
def softmax(x):
if x.ndim == 2:
x = x.T
x = x - np.max(x, axis=0)
y = np.exp(x) / np.sum(np.exp(x), axis=0)
return y.T
x = x - np.max(x) #溢出对策
return np.exp(x) / np.sum(np.exp(x))2.6、其他常见函数
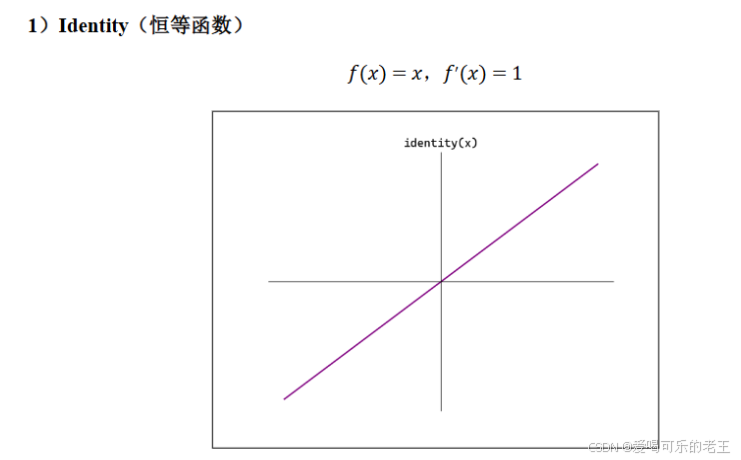
3、如何选择激活函数
1)隐藏层
- 首选ReLU,如果效果不好可尝试Leaky ReLU等。
- Sigmoid在隐藏层易导致梯度消失,应尽量避免。
- Tamh 的输出均值为0,对中心化数据更友好,但仍可能引发梯度消失,仅适用于浅层网络。
2)输出层
- 二分类选择 Sigmoid。
- 多分类选择 Softmax。
- 回归默认选择 Identity。
4、神经网络简单实现
深度神经网络由多个层(layer)组成,通常将其称之为 模型(Model)。整个模型接受原始 输入(特征),生成 输出(预测),并包含一些 参数。而在模型内部,每个单独的层都会接受一些输入(由前一层提供),生成输出(到下一层的输入),并包含一组参数;层层向下传递,就可以得到最终的输出值。神经网络中的参数,就是每一层的权重和偏置。
4.1、三层神经网络
这里以一个三层神经网络为例,从输入到输出的处理计算,这个过程就是前向传播(forward)。
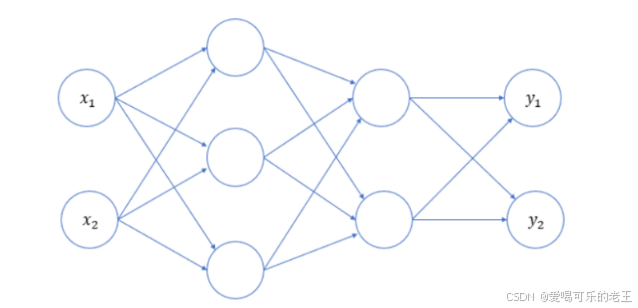
简单起见,我们的输入层(第0层)有2个神经元;第1个隐藏层(第1层)有3个神经元;第2个隐藏层(第2层)有2个神经元;输出层(第3层)有2个神经元。
4.2、各层之间的信号传输
上面只是三层网络的示意图,实际上每层还应该有偏置,各输入信号加权总和还要经过激活函数的处理。接下来逐层进行分析,考察信号在各层之间传递的过程。
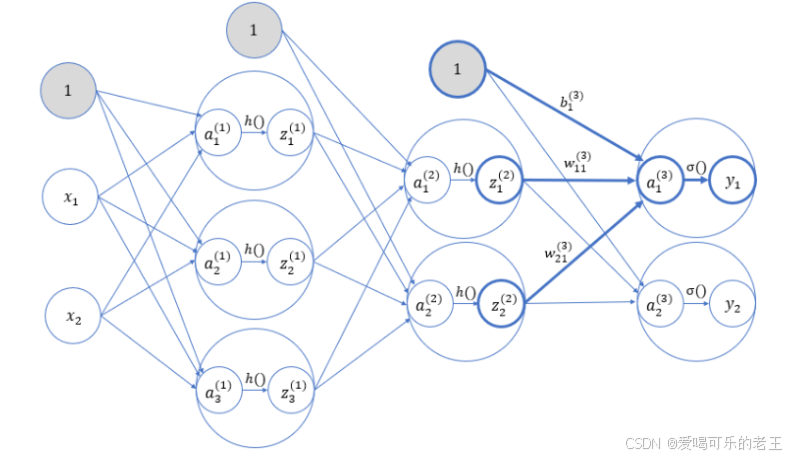
权重和神经元的上标(1)表示网络层号。而下标对于神经元来说,就是这一层内的"索引号";对于权重来说则包含两个数字,分别代表前一层和后一层神经元的索引号。所以,w(1)21 就表示这是第 1 层的权重(输入层到第 1 层),并且是从第 2 个输入节点到第 1 层第 1个节点。偏置的下标只有 1 个,因为前一层的偏置节点只有一个。
5、简单代码实现
我们可以将神经网络的所有参数(每一层的权重 w 和偏置 b),保存在一个字典 network中;并定义函数:
- init_network():对参数进行初始化,每一个权重参数都是一个矩阵(二维),每一个偏置参数则是一个数组(一维);
- forward():前向传播,将输入信号转换为输出信号的处理操作。这里的激活函数,隐藏层用 sigmoid,输出层用 identity(恒等函数)。
具体代码如下:
import numpy as np
from conmen.step_function import sigmoid,identity
#初始化神经网络
def init_network():
network = {}
network["W1"] = np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]])
network["b1"] = np.array([0.1,0.2,0.3])
network["W2"] = np.array([[0.1,0.4],[0.2,0.5],[0.3,0.6]])
network["b2"] = np.array([0.1,0.2])
network["W3"] = np.array([[0.1,0.3],[0.2,0.4]])
network["b3"] = np.array([0.1,0.2])
return network
#前向传播
def forward(network,X):
W1,W2,W3 = network["W1"],network["W2"],network["W3"]
b1,b2,b3 = network["b1"],network["b2"],network["b3"]
a1 = np.dot(X,W1) + b1 # 矩阵乘法
z1 = sigmoid(a1)
a2 = np.dot(z1,W2) + b2 # 矩阵乘法
z2 = sigmoid(a2)
a3 = np.dot(z2,W3) + b3 # 矩阵乘法
y = identity(a3)
return y
network = init_network()
X = np.array([1.0,0.5])
y = forward(network,X)
print(y)