算法---常见位运算总结

1.基础位运算

①<<：左移操作符

②>>：右移操作符

③~：取反运算符

④&：与，有0就是0

⑤| ：或，有1就是1

⑥^：异或，相同为0，相异为1/无进位相加

2.给一个数n，确定他的二进制表示中的第x位是0还是1

①n&(1<<x)

②(n>>x)&1

3.将一个数n的二进制表示的第x位修改成1

n |= (1<<x)

4.将一个数n的二进制表示的第x位修改成0

n &= ~(1<<x)

5.提取一个数n二进制表示中最右侧的1

①解释 lowbit

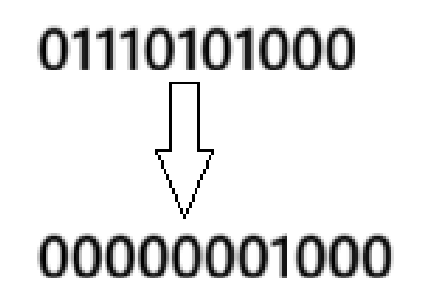
②操作

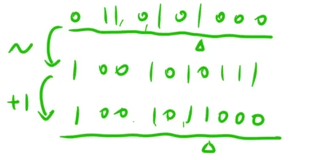
n&-n

-n：先取反再加一，本质是将最右侧的1，左侧区域的区域全部取反

6.干掉一个数n二进制表示中的最右侧的1

n&(n-1)

n-1: 本质是将最右侧的1右边的区域(包含1)全部变成相反

191. 位1的个数 - 力扣（LeetCode）

cpp 复制代码

class Solution {
public:
    int hammingWeight(int n) {
        int ret = 0;
        while(n)
        {
            n&=(n-1);
            ret++;
        }
        return ret;
    }
};

338. 比特位计数 - 力扣（LeetCode）

cpp 复制代码

class Solution {
public:
    vector<int> countBits(int n) {
        vector<int> ret(n+1);
        for(int i = 1; i <= n; i++)
        {
            int tmp = i;
            int cnt = 0;
            while(tmp)
            {
                tmp&=(tmp-1);
                cnt++;
            }
            ret[i] = cnt;
        }
        return ret;
    }
};

461. 汉明距离 - 力扣（LeetCode）

cpp 复制代码

class Solution {
public:
    int hammingDistance(int x, int y) {
        int ret = 0;
        while(x || y)
        {
            int tmp1 = x & 1;
            int tmp2 = y & 1;
            x = x >> 1;
            y = y >> 1;
            if(tmp1 != tmp2) ret++;
        }
        return ret;
    }
};

7.异或运算的运算律

①a ^ 0 = a

②a ^ a = 0

③a ^ b ^ c = a ^ (b ^ c)交换律

136. 只出现一次的数字 - 力扣（LeetCode）

cpp 复制代码

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int ret = nums[0];
        for(int i = 1; i < nums.size(); i++)
        {
            ret^=nums[i];
        }
        return ret;
    }
};

原理：a ⊕ b ⊕ a = b ⊕ a ⊕ a = b ⊕ ( a ⊕ a ) = b ⊕ 0 = b。

260. 只出现一次的数字 III - 力扣（LeetCode）

cpp 复制代码

vector<int> singleNumber(vector<int>& nums) {
        //1.求出两个数的异或值
        int a = 0;
        int b = 0;
        int x = 0;
        for(auto e : nums)
            x ^= e;
        //2.找出xor最右侧的1，也就是a和b从右往左数第一个不同的位置
        int div = 1;
        while((x & div) == 0)
            div = div<<1;
        //3.遍历，分组，不同位置为1的和不同位置为0的
        for(auto e : nums)
        {
            if((e & div) == 0)
                a^=e;
            else
                b^=e;
        }
        return vector<int>{a,b};
    }

思路：①相同的数异或后为0，将全部数异或后得到只出现1次的数的异或值

②找出异或值最右侧的1，这个位置就是两个返回值的第一个二进制不同位

③将nums分为两组，不同位为1的和不同位为0的，再进行异或，这样就肯定能将返回值分为两组，从而得到返回值